Generating Names and Classifying Names with Character-Level RNN

原文地址:  Generating Names with Character-Level RNN

搬运只为督促自己学习,没有其他目的。

Preparing the Data

Download the data from here and extract it to the current directory

In short, there are a bunch of plain text files data/names/[Language].txt with a name per line. We split lines into an array, convert Unicode to ASCII, and end up with a dictionary {language: [names ...]}.

from __future__ import unicode_literals, print_function, division
from io import open
import glob
import os
import unicodedata
import string

all_letters = string.ascii_letters + " .,;'-"
n_letters = len(all_letters) + 1 # Plus EOS marker

def findFiles(path): return glob.glob(path)

# Turn a Unicode string to plain ASCII, thanks to http://stackoverflow.com/a/518232/2809427
def unicodeToAscii(s):
    return ''.join(
        c for c in unicodedata.normalize('NFD', s)
        if unicodedata.category(c) != 'Mn'
        and c in all_letters
    )

# Read a file and split into lines
def readLines(filename):
    lines = open(filename, encoding='utf-8').read().strip().split('
')
    return [unicodeToAscii(line) for line in lines]

# Build the category_lines dictionary, a list of lines per category
category_lines = {}
all_categories = []
for filename in findFiles('data/names/*.txt'):
    category = os.path.splitext(os.path.basename(filename))[0]
    all_categories.append(category)
    lines = readLines(filename)
    category_lines[category] = lines

n_categories = len(all_categories)

if n_categories == 0:
    raise RuntimeError('Data not found. Make sure that you downloaded data '
        'from https://download.pytorch.org/tutorial/data.zip and extract it to '
        'the current directory.')

print('# categories:', n_categories, all_categories)
print(unicodeToAscii("O'Néàl"))

Creating the Network

The category tensor is a one-hot vector just like the letter input.

We will interpret the output as the probability of the next letter. When sampling, the most likely output letter is used as the next input letter.

import torch
import torch.nn as nn

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()
        self.hidden_size = hidden_size

        self.i2h = nn.Linear(n_categories + input_size + hidden_size, hidden_size)
        self.i2o = nn.Linear(n_categories + input_size + hidden_size, output_size)
        self.o2o = nn.Linear(hidden_size + output_size, output_size)
        self.dropout = nn.Dropout(0.1)
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, category, input, hidden):
        input_combined = torch.cat((category, input, hidden), 1)
        hidden = self.i2h(input_combined)
        output = self.i2o(input_combined)
        output_combined = torch.cat((hidden, output), 1)
        output = self.o2o(output_combined)
        output = self.dropout(output)
        output = self.softmax(output)
        return output, hidden

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)

Training

Preparing for Training

First of all, helper functions to get random pairs of (category, line):

import random

# Random item from a list
def randomChoice(l):
    return l[random.randint(0, len(l) - 1)]

# Get a random category and random line from that category
def randomTrainingPair():
    category = randomChoice(all_categories)
    line = randomChoice(category_lines[category])
    return category, line

For each timestep (that is, for each letter in a training word) the inputs of the network will be (category, current letter, hidden state) and the outputs will be (next letter, next hidden state). So for each training set, we’ll need the category, a set of input letters, and a set of output/target letters.

The category tensor is a one-hot tensor of size <1 x n_categories>. When training we feed it to the network at every timestep - this is a design choice, it could have been included as part of initial hidden state or some other strategy.

# One-hot vector for category
def categoryTensor(category):
    li = all_categories.index(category)
    tensor = torch.zeros(1, n_categories)
    tensor[0][li] = 1
    return tensor

# One-hot matrix of first to last letters (not including EOS) for input
def inputTensor(line):
    tensor = torch.zeros(len(line), 1, n_letters)
    for li in range(len(line)):
        letter = line[li]
        tensor[li][0][all_letters.find(letter)] = 1
    return tensor

# LongTensor of second letter to end (EOS) for target
def targetTensor(line):
    letter_indexes = [all_letters.find(line[li]) for li in range(1, len(line))]
    letter_indexes.append(n_letters - 1) # EOS
    return torch.LongTensor(letter_indexes)

For convenience during training we’ll make a randomTrainingExample function that fetches a random (category, line) pair and turns them into the required (category, input, target) tensors.

# Make category, input, and target tensors from a random category, line pair
def randomTrainingExample():
    category, line = randomTrainingPair()
    category_tensor = categoryTensor(category)
    input_line_tensor = inputTensor(line)
    target_line_tensor = targetTensor(line)
    return category_tensor, input_line_tensor, target_line_tensor

Training the Network

In contrast to classification, where only the last output is used, we are making a prediction at every step, so we are calculating loss at every step.

The magic of autograd allows you to simply sum these losses at each step and call backward at the end.

criterion = nn.NLLLoss()

learning_rate = 0.0005

def train(category_tensor, input_line_tensor, target_line_tensor):
    target_line_tensor.unsqueeze_(-1)
    hidden = rnn.initHidden()

    rnn.zero_grad()

    loss = 0

    for i in range(input_line_tensor.size(0)):
        output, hidden = rnn(category_tensor, input_line_tensor[i], hidden)
        l = criterion(output, target_line_tensor[i])
        loss += l

    loss.backward()

    for p in rnn.parameters():
        p.data.add_(-learning_rate, p.grad.data)

    return output, loss.item() / input_line_tensor.size(0)

To keep track of how long training takes I am adding a timeSince(timestamp) function which returns a human readable string:

import time
import math

def timeSince(since):
    now = time.time()
    s = now - since
    m = math.floor(s / 60)
    s -= m * 60
    return '%dm %ds' % (m, s)

Training is business as usual - call train a bunch of times and wait a few minutes, printing the current time and loss every print_every examples, and keeping store of an average loss per plot_every examples in all_losses for plotting later.

rnn = RNN(n_letters, 128, n_letters)

n_iters = 100000
print_every = 5000
plot_every = 500
all_losses = []
total_loss = 0 # Reset every plot_every iters

start = time.time()

for iter in range(1, n_iters + 1):
    output, loss = train(*randomTrainingExample())
    total_loss += loss

    if iter % print_every == 0:
        print('%s (%d %d%%) %.4f' % (timeSince(start), iter, iter / n_iters * 100, loss))

    if iter % plot_every == 0:
        all_losses.append(total_loss / plot_every)
        total_loss = 0

Plotting the Losses

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

plt.figure()
plt.plot(all_losses)

Sampling the Network

To sample we give the network a letter and ask what the next one is, feed that in as the next letter, and repeat until the EOS token.

• Create tensors for input category, starting letter, and empty hidden state
• Create a string output_name with the starting letter
• Up to a maximum output length,
  • Feed the current letter to the network
  • Get the next letter from highest output, and next hidden state
  • If the letter is EOS, stop here
  • If a regular letter, add to output_name and continue
• Return the final name

Note:Rather than having to give it a starting letter, another strategy would have been to include a “start of string” token in training and have the network choose its own starting letter.

max_length = 20

# Sample from a category and starting letter
def sample(category, start_letter='A'):
    with torch.no_grad():  # no need to track history in sampling
        category_tensor = categoryTensor(category)
        input = inputTensor(start_letter)
        hidden = rnn.initHidden()

        output_name = start_letter

        for i in range(max_length):
            output, hidden = rnn(category_tensor, input[0], hidden)
            topv, topi = output.topk(1)
            topi = topi[0][0]
            if topi == n_letters - 1:
                break
            else:
                letter = all_letters[topi]
                output_name += letter
            input = inputTensor(letter)

        return output_name

# Get multiple samples from one category and multiple starting letters
def samples(category, start_letters='ABC'):
    for start_letter in start_letters:
        print(sample(category, start_letter))

samples('Russian', 'RUS')

samples('German', 'GER')

samples('Spanish', 'SPA')

samples('Chinese', 'CHI')

原文地址:  Classifying Names with Character-Level RNN

搬运只为督促自己学习,没有其他目的。

Preparing the Data

Data is the same as the previous!

from __future__ import unicode_literals, print_function, division
from io import open
import glob
import os

def findFiles(path): return glob.glob(path)

print(findFiles('data/names/*.txt'))

import unicodedata
import string

all_letters = string.ascii_letters + " .,;'"
n_letters = len(all_letters)

# Turn a Unicode string to plain ASCII, thanks to http://stackoverflow.com/a/518232/2809427
def unicodeToAscii(s):
    return ''.join(
        c for c in unicodedata.normalize('NFD', s)
        if unicodedata.category(c) != 'Mn'
        and c in all_letters
    )

print(unicodeToAscii('Ślusàrski'))

# Build the category_lines dictionary, a list of names per language
category_lines = {}
all_categories = []

# Read a file and split into lines
def readLines(filename):
    lines = open(filename, encoding='utf-8').read().strip().split('
')
    return [unicodeToAscii(line) for line in lines]

for filename in findFiles('data/names/*.txt'):
    category = os.path.splitext(os.path.basename(filename))[0]
    all_categories.append(category)
    lines = readLines(filename)
    category_lines[category] = lines

n_categories = len(all_categories)

Now we have category_lines, a dictionary mapping each category (language) to a list of lines (names). We also kept track of all_categories (just a list of languages) and n_categories for later reference.

Turning Names into Tensors

Now that we have all the names organized, we need to turn them into Tensors to make any use of them.

To represent a single letter, we use a “one-hot vector” of size <1 x n_letters>. A one-hot vector is filled with 0s except for a 1 at index of the current letter, e.g. "b" = <0 1 0 0 0 ...>.

To make a word we join a bunch of those into a 3D matrix <line_length x 1 x n_letters>.

That extra 1 dimension is because PyTorch assumes everything is in batches - we’re just using a batch size of 1 here.

import torch

# Find letter index from all_letters, e.g. "a" = 0
def letterToIndex(letter):
    return all_letters.find(letter)

# Just for demonstration, turn a letter into a <1 x n_letters> Tensor
def letterToTensor(letter):
    tensor = torch.zeros(1, n_letters)
    tensor[0][letterToIndex(letter)] = 1
    return tensor

# Turn a line into a <line_length x 1 x n_letters>,
# or an array of one-hot letter vectors
def lineToTensor(line):
    tensor = torch.zeros(len(line), 1, n_letters)
    for li, letter in enumerate(line):
        tensor[li][0][letterToIndex(letter)] = 1
    return tensor

print(letterToTensor('J'))

print(lineToTensor('Jones').size())

Creating the Network

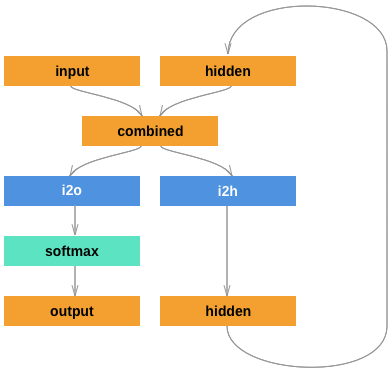
import torch.nn as nn

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()

        self.hidden_size = hidden_size

        self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
        self.i2o = nn.Linear(input_size + hidden_size, output_size)
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input, hidden):
        combined = torch.cat((input, hidden), 1)
        hidden = self.i2h(combined)
        output = self.i2o(combined)
        output = self.softmax(output)
        return output, hidden

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)

n_hidden = 128
rnn = RNN(n_letters, n_hidden, n_categories)

To run a step of this network we need to pass an input (in our case, the Tensor for the current letter) and a previous hidden state (which we initialize as zeros at first). We’ll get back the output (probability of each language) and a next hidden state (which we keep for the next step).

input = letterToTensor('A')
hidden =torch.zeros(1, n_hidden)

output, next_hidden = rnn(input, hidden)

For the sake of efficiency we don’t want to be creating a new Tensor for every step, so we will use lineToTensor instead of letterToTensor and use slices. This could be further optimized by pre-computing batches of Tensors.

input = lineToTensor('Albert')
hidden = torch.zeros(1, n_hidden)

output, next_hidden = rnn(input[0], hidden)
print(output)

As you can see the output is a <1 x n_categories> Tensor, where every item is the likelihood of that category (higher is more likely).

Training

Preparing for Training

Before going into training we should make a few helper functions. The first is to interpret the output of the network, which we know to be a likelihood of each category. We can use Tensor.topk to get the index of the greatest value:

def categoryFromOutput(output):
    top_n, top_i = output.topk(1)
    category_i = top_i[0].item()
    return all_categories[category_i], category_i

print(categoryFromOutput(output))

A quick way to get a training example (a name and its language):

import random

def randomChoice(l):
    return l[random.randint(0, len(l) - 1)]

def randomTrainingExample():
    category = randomChoice(all_categories)
    line = randomChoice(category_lines[category])
    category_tensor = torch.tensor([all_categories.index(category)], dtype=torch.long)
    line_tensor = lineToTensor(line)
    return category, line, category_tensor, line_tensor

for i in range(10):
    category, line, category_tensor, line_tensor = randomTrainingExample()
    print('category =', category, '/ line =', line)

Training the Network

Now all it takes to train this network is show it a bunch of examples, have it make guesses, and tell it if it’s wrong.

For the loss function nn.NLLLoss is appropriate, since the last layer of the RNN is nn.LogSoftmax.

Each loop of training will:

• Create input and target tensors
• Create a zeroed initial hidden state
• Read each letter in and
  • Keep hidden state for next letter
• Compare final output to target
• Back-propagate
• Return the output and loss

criterion = nn.NLLLoss() #Negative log likelihood loss It is useful to train a classification problem with C classes.
learning_rate = 0.005 # If you set this too high, it might explode. If too low, it might not learn

def train(category_tensor, line_tensor):
    hidden = rnn.initHidden()

    rnn.zero_grad()

    for i in range(line_tensor.size()[0]):
        output, hidden = rnn(line_tensor[i], hidden)

    loss = criterion(output, category_tensor)
    loss.backward()

    # Add parameters' gradients to their values, multiplied by learning rate
    for p in rnn.parameters():
        p.data.add_(-learning_rate, p.grad.data)

    return output, loss.item()

Now we just have to run that with a bunch of examples. Since the train function returns both the output and loss we can print its guesses and also keep track of loss for plotting. Since there are 1000s of examples we print only every print_every examples, and take an average of the loss.

import time
import math

n_iters = 100000
print_every = 5000
plot_every = 1000



# Keep track of losses for plotting
current_loss = 0
all_losses = []

def timeSince(since):
    now = time.time()
    s = now - since
    m = math.floor(s / 60)
    s -= m * 60
    return '%dm %ds' % (m, s)

start = time.time()

for iter in range(1, n_iters + 1):
    category, line, category_tensor, line_tensor = randomTrainingExample()
    output, loss = train(category_tensor, line_tensor)
    current_loss += loss

    # Print iter number, loss, name and guess
    if iter % print_every == 0:
        guess, guess_i = categoryFromOutput(output)
        correct = '✓' if guess == category else '✗ (%s)' % category
        print('%d %d%% (%s) %.4f %s / %s %s' % (iter, iter / n_iters * 100, timeSince(start), loss, line, guess, correct))

    # Add current loss avg to list of losses
    if iter % plot_every == 0:
        all_losses.append(current_loss / plot_every)
        current_loss = 0

Plotting the Results

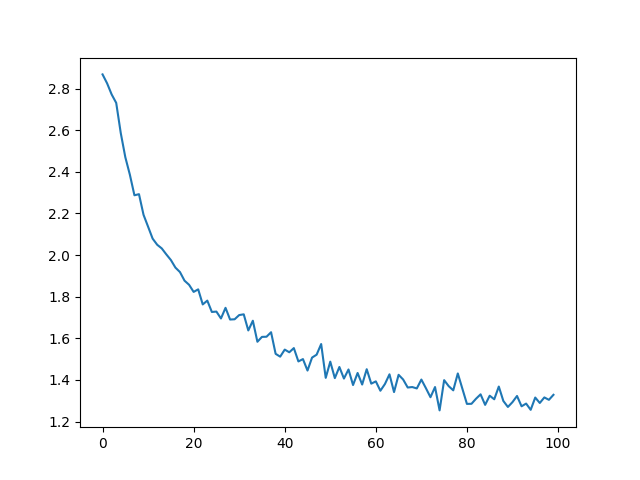
Plotting the historical loss from all_losses shows the network learning:

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

plt.figure()
plt.plot(all_losses)

Evaluating the Results

To see how well the network performs on different categories, we will create a confusion matrix, indicating for every actual language (rows) which language the network guesses (columns). To calculate the confusion matrix a bunch of samples are run through the network with evaluate(), which is the same as train() minus the backprop.

# Keep track of correct guesses in a confusion matrix
confusion = torch.zeros(n_categories, n_categories)
n_confusion = 10000

# Just return an output given a line
def evaluate(line_tensor):
    hidden = rnn.initHidden()

    for i in range(line_tensor.size()[0]):
        output, hidden = rnn(line_tensor[i], hidden)

    return output

# Go through a bunch of examples and record which are correctly guessed
for i in range(n_confusion):
    category, line, category_tensor, line_tensor = randomTrainingExample()
    output = evaluate(line_tensor)
    guess, guess_i = categoryFromOutput(output)
    category_i = all_categories.index(category)
    confusion[category_i][guess_i] += 1

# Normalize by dividing every row by its sum
for i in range(n_categories):
    confusion[i] = confusion[i] / confusion[i].sum()

# Set up plot
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(confusion.numpy())
fig.colorbar(cax)

# Set up axes
ax.set_xticklabels([''] + all_categories, rotation=90)
ax.set_yticklabels([''] + all_categories)

# Force label at every tick
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))

# sphinx_gallery_thumbnail_number = 2
plt.show()

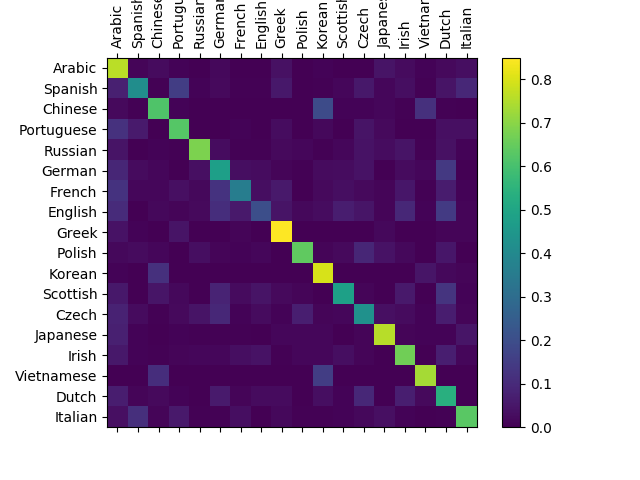
You can pick out bright spots off the main axis that show which languages it guesses incorrectly, e.g. Chinese for Korean, and Spanish for Italian. It seems to do very well with Greek, and very poorly with English (perhaps because of overlap with other languages).

Running on User Input

def predict(input_line, n_predictions=3):
    print('
> %s' % input_line)
    with torch.no_grad():
        output = evaluate(lineToTensor(input_line))

        # Get top N categories
        topv, topi = output.topk(n_predictions, 1, True)
        predictions = []

        for i in range(n_predictions):
            value = topv[0][i].item()
            category_index = topi[0][i].item()
            print('(%.2f) %s' % (value, all_categories[category_index]))
            predictions.append([value, all_categories[category_index]])

predict('Dovesky')
predict('Jackson')
predict('Satoshi')