python函数—调用函数+定义函数

抽象

函数就是最基本的一种代码抽象的方式。

调用函数

可以通过help(abs)查看abs函数的帮助信息

abs(x)  : return position number
# 常见报错：abs() takes exactly one argument (2 given        )abs()有且仅有1个参数, 不能为两个
# TypeError: bad operand type for abs(): 'str' str是错误的参数类型
max() : return the max of the argument
# max()可以接收任意多个参数，并返回最大的那个
int() ,float() ,bool(), str() ,float()
#常用函数还包括数据类型转换函数，可以把其他数据类型转换为对应类型

# 函数名其实就是指向一个函数对象的引用，完全可以把函数名赋给一个变量，相当于给这个函数起了一个“别名”：
a = max
print(a(1,2,3))

# hex()函数把一个整数转换成十六进制表示的字符串
print(hex(123))
#0x7b

print(sum([1,2,3,4]))
#10 这里参数要一个列表集合

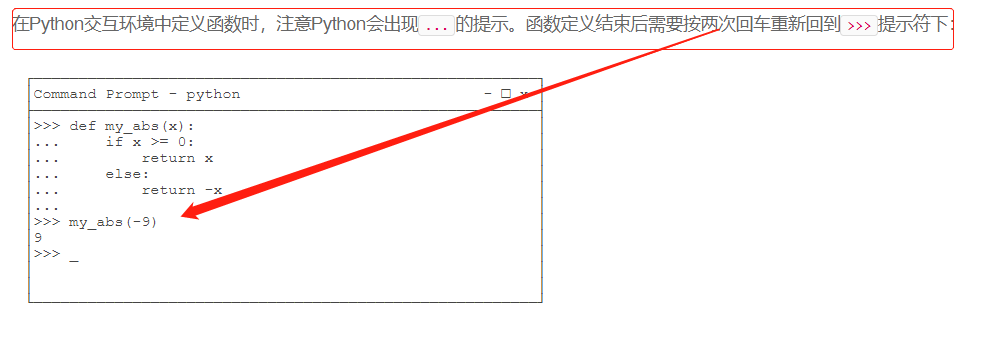
定义函数

Python中，定义一个函数要使用def语句，依次写出函数名、括号、括号中的参数和冒号:，然后，在缩进块中编写函数体，函数的返回值用return语句返回

def boolean_position_num(x):
    if x >= 0 :
        return True
    else :
        return False

print(boolean_position_num(int(input())))

函数体内部的语句在执行时，一旦执行到return时，函数就执行完毕，并将结果返回。因此，函数内部通过条件判断和循环可以实现非常复杂的逻辑。
如果没有return语句，函数执行完毕后也会返回结果，只是结果为None。return None可以简写为return

def boolean_position_num(x):
    if x >= 0 :
       print('position num')
    else :
        print('not position num')
# 默认return None

print(boolean_position_num(int(input())))
# 10  None

命令行格式

#调用别的文件里的函数
# main.py
from func import boolean_position_num
print(boolean_position_num(int(input())))

# func.py
def boolean_position_num(x):
    if x >= 0 :
       print('position num')
    else :
        print('not position num')

空函数

#定义一个什么事也不做的空函数，可以用pass语句
def non():
    pass
#pass可以用来作为占位符，比如现在还没想好怎么写函数的代码，就可以先放一个pass，让代码能运行起来。不加pass就会报错
if x >= 18:
     pass

参数检查

TypeError: my_abs() takes 1 positional argument but 2 were given : 参数数量不对
自己写的函数跟内置函数的区别为：自己写的函数很多都不能支持其他的数据类型，内置函数可以
数据类型检查可以用内置函数isinstance()实现：

def my_abs(x):
    if not isinstance(x, (int, float)):
        raise TypeError('bad operand type')        
    if x >= 0:
        return x
    else:
        return -x

返回多个值? 只是返回一个tuple值 Python函数返回的仍然是单一值。

用途：在游戏中经常需要从一个点移动到另一个点，给出坐标、位移和角度，就可以计算出新的坐标：

def return_nums(x , y):
    return int(x),int(y)
if __name__ == '__main__':
    print(return_nums(1,2))
# (1 , 2)

小结

定义函数时，需要确定函数名和参数个数；
如果有必要，可以先对参数的数据类型做检查；
函数体内部可以用return随时返回函数结果；
函数执行完毕也没有return语句时，自动return None。
函数可以同时返回多个值，但其实就是一个tuple。

练习

ax^2+bx+c=0

from cmath import sqrt
def quadratic(a, b, c):
    a = float(a)
    b = float(b)
    c = float(c)
    temp = pow(b, 2) - 4 * a * c
    if temp<0 :
        print('该方程无解')
    x1 = (-b + (sqrt(temp))) / (2 * a)
    x2 = (-b - (sqrt(temp))) / (2 * a)
    if temp == 0:
        print('该方程只有一个解')
        return x1
    return x1, x2
if __name__ == '__main__':
    print('quadratic(2, 3, 1) =', quadratic(2, 3, 1))
    print('quadratic(1, 3, -4) =', quadratic(1, 3, -4))

    if quadratic(2, 3, 1) != (-0.5, -1.0):
        print('测试失败')
    elif quadratic(1, 3, -4) != (1.0, -4.0):
        print('测试失败')
    else:
        print('测试成功')
-------------------------------------------------------------------------------
import cmath
def quadratic(a,b,c):

     if not (isinstance(a,(int,float) ) and isinstance(b,(int,float)) and isinstance(c,(int,float)) ):

         raise TypeError('bad operation type')

     elif b**2-4*a*c < 0 :

         print('该方程没有实数解')

     else :

         x1 = (-b + math.sqrt(b**2-4*a*c))/(2*a)

         x2 = (-b - math.sqrt(b**2-4*a*c))/(2*a)

         return x1, x2

print(quadratic(3,5,1))

print(quadratic(a,c,1))