zoukankan html css js c++ java

排序系列及其拓展优化（Java实现）

一、插入排序

1. 算法思想：设一共有n个元素，对于第i轮排序，在第i到第n个元素中找到最大值x，将x放在第i个位置。

2. 时间复杂度：要执行n轮排序，每次以O（n）时间寻找最值，时间复杂度O（n²）

3. 空间复杂度：不需要开辟额外空间 O（1）

4. 优点：简单

5. 缺点：时间复杂度过高，最好情况和最坏情况都是O（n²）

6. 代码描述

package sort;

import java.util.Random;

public class Example {
    
    //选择排序
    public static void selectSort(Comparable[] a) {
        for(int i=0; i<a.length; i++) {
            Comparable min = a[i];//记录该轮排序的最小值
            int pos = i;//记录最小值的位置
            for(int j=i+1; j<a.length; j++) {
                if(cmp(a[j] , a[pos]) < 0) {
                    pos = j;
                    min = a[j];
                }
            }
            exch(a, i, pos);//对a数组交换第i和第pos元素的位置
        }
    }
    
    //交换函数，交换a数组中i,j两位置
    public static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
    
    //打印元素的值
    //如果是对象要重写一下toString方法
    public static void show(Comparable[] a) {
        for(Comparable t  : a)
            System.out.print(t.toString() + " ");
        System.out.println();
    }
    
    //比较函数   可以自定义比较关键字
    //注意，该对象需要实现Comparable接口并且重写compareTo方法
    private static int cmp(Comparable a, Comparable b) {
        // TODO Auto-generated method stub
        return a.compareTo(b);
    }
    
    public static void main(String[] args)  {
        // TODO Auto-generated method stub
        Random random = new Random(10);
        Comparable[] a = new Integer[100];//Integer内部实现了Comparable接口
        for(int i=0; i<100; i++) {
            a[i] = random.nextInt(1000);
        }
        show(a);//排序前
        selectSort(a);
        show(a);//排序后
    }
    
}

二、插入排序

1. 算法思想：

(1) 设一共有n个元素，对于第i轮排序，前i-1个元素已经排好序，那么寻找在第1个到第i-1个元素中寻找一个位置将第i个元素插进去，类似于打扑克。

很显然，如果找到一个插入位置x∈[1,i-1],那么设t=a[i] 从第x到第i-1所有元素都要向后移一位，把第x位置空出来后再插入第i个元素t

(2) 上面的方法可以改进使得代码比较简单，设t=a[i]，既然需要后移，可以每一步都将t与左边元素的值比较，如果左边的大就与左边元素互换位置，直到左边的元素不大于t，省去挪位置。

2. 时间复杂度：

（1）最坏情况下即逆序情况下，每一轮插入值都需要插到最前面，复杂度O（n²)

（2）如果元素基本有序，复杂度接近O（n）

3. 空间复杂度：不需要开辟额外空间 O（1）

4. 优点：简单,适合基本有序的数组的排序，时间复杂度接近线性

5. 缺点：依赖数组初始情况，最坏情况是O（n²）

6. 代码描述

    //插入排序
    public static void insertSort(Comparable[] a) {
        for(int i=1; i<a.length; i++) {//把第一个数看做是有序的，从第二个数开始
            for(int j=i; j>0; j--) {//寻找插入位置
                if(cmp(a[j] , a[j-1]) >= 0) {//发现前面的数比它小，那说明位置已经找到了，不需要再找
                    break;
                }
                else {//否则不断与相邻元素交换位置
                    exch(a , j, j-1);
                }
            }
        }
    }

三、希尔排序

1. 算法思想：

(1) 首先介绍什么是h有序数组，一个数组是h有序数组，则这个数组可以拆分成h个互不相交的间隔一致为h的有序子数组（相对顺序不变），比如

2 3 19 5 4 21 10 8 48 12 66 57

可以拆分成h = 3的有序子数组

2 5 10 12

3 4 8 66

19 21 48 57

（2）希尔排序的思想就是是数组中任意间隔为h的元素都是有序的。h选取一个数列，逐步迭代直至为1，那么这个数组就是全部有序的了。

（3）不难看出，可以在插入排序的基础上，对每一个h数组进行实现。

2. 时间复杂度：

根据选取的h序列（递增序列）不同，复杂度不一样，而且难以计算，只能评估一个下限，希尔斯排序复杂度O（N^4/3）O（N^5/4）等等

3. 空间复杂度：不需要开辟额外空间 O（1）

4. 优点：克服了插入排序需要频繁交换的问题，适合大规模排序，原因是平衡了子数组的规模和有序性。

5. 缺点：速度没有特别快。

6. 代码描述

    //希尔排序 
    public static void shellSort(Comparable[] a ) {
        //构造h
        int h = 1;
        int n = a.length;
        while(h <= n/3) h = h*3+1;// h = 1 4 13 40 121...
        while(h >= 1) { //每一轮使原数组变成h有序数组
            for(int i=h; i<n; i++) { //插入排序的变形，之前是两两相邻，现在是h相邻
                for(int j=i; j>=h && cmp(a[j] , a[j-h]) < 0; j-=h) { //
                    exch(a , j , j-h); //
                }
            }
            h = h/3;//h收缩，直至1，此时的h有序数组就是有序数组
        }
    }

四、归并排序

1. 算法思想：

(1) 假如有一个数组，左半边是有序的，右半边也是有序的，那么如何把它们整体变为有序呢？

(2) 很显然，只要对左右两边每次挑一个较小的出来，直到左边挑完或者右边挑完，把剩余部分直接接在已经排好序的数列的尾部就可以了。

(3)递归地使用（1）（2）即可，图示出处：https://www.cnblogs.com/skywang12345/p/3602369.html

2. 时间复杂度：

（1）需要二分logN次，每次归并是线性复杂度，总体是O（NlogN）

3. 空间复杂度：需要开辟额外空间 O（N），用于辅助数组aux, 函数递归调用的栈空间O(logN)，总体空间复杂度O（N）

4. 优点：速度快

5. 缺点：空间复杂度高

6. 代码描述

    //归并排序
    private static Comparable[] aux;
    //merge方法
    public static void merge(Comparable[] a,  int lo, int mid , int hi) {
        int p = lo, q = mid+1;
        for(int i=lo; i<=hi; i++) aux[i] = a[i];
        int cnt = lo;
        while( p <= mid && q <= hi) {
            
            if(cmp(aux[p] , aux[q]) < 0) a[cnt++] = aux[p++];
            else a[cnt++] = aux[q++];
        }
        while(p <= mid) a[cnt++] = aux[p++];
        while(q <= hi) a[cnt++] = aux[q++];
    }
    
    //sort方法
    public static void sort(Comparable[] a, int lo, int hi) {
        if(lo >= hi) return ; //如果low > high则返回
        int mid = lo + ((hi - lo) >> 1);//取中间点为中点 
        sort(a , lo , mid);//对左边的归并
        sort(a , mid + 1, hi);//对右边的归并
        merge(a , lo , mid , hi);//左右归并好了则归并到一起
    }
    //启动函数
    public static void mergeSort(Comparable[] a) {
        aux = new Comparable[a.length];
        sort(a , 0, a.length - 1);
    }

【小插曲】

一开始运行一直报栈溢出的错误，指示在sort方法中 sort(a , lo , mid);这一行，debug时发现有时候mid比lo还小，说明是mid运算那一行出错了，

一开始 int mid = lo + (hi - lo) >> 1; 后来查到两点关于移位操作的知识

(1) 原本右移一位等价于将整数除以2，现在发现对于负奇数不成立，原因是移位和除法截断方式不一样，

比如 -7 / 2 = -3 ，但-7 >> 1 = -4

(2) 移位优先级比加减要低，此处错误源于这一点

【拓展】自顶向下与自底向上的归并排序

（1）事实上，上述方法是自顶向下分解原数组到每组1个数，然后调用merge回溯

（2）其实也可以首先将原数组分解，分组大小从1到2到4到2ⁱ , 自底向上归并。只需要修改sort函数

//from bottom to up
    public static void mergeSortBU(Comparable[] a) {
        int n = a.length;
        aux = new Comparable[n];
        for(int sz = 1; sz < n; sz += sz) {
            for(int lo = 0; lo < n - sz + 1; lo += sz+sz) {
                merge(a , lo, lo+sz-1, Math.min(lo+sz+sz-1 , n-1));
            }
        }
    }

五、快速排序

1. 算法思想

（1）快速排序的主要思想和归并排序类似，都是分治，都是左边部分有序，右边部分有序，再整体有序。但是快速排序的切分点是不稳定的，并不总是中点。

（2）对于快速排序，其切分策略是，总是找当前范围内第一个数x应该处于的位置k，即a[lo]~a[k-1]小于等于x，a[k+1]~a[hi]都大于等于x，找位置K的方法是，从两头往中间夹逼，

途中如果发现一对左边大于x的数和右边小于x的数便将它们交换，直到两头碰到为止。这样一来就实现了对于位置K而言，左边的数都不比他大，右边的数都不比他小。

（3）分别对a[lo]~a[k-1]和a[k+1]~a[hi]递归地使用（1）（2），可以证明每个数都“各得其所”，数组也就整体有序了。

2. 时间复杂度：O（NlogN）

3. 空间复杂度：不需要开辟额外空间 O（1），但是需要额外的平均栈空间O（logN），最多退化到O（N）。

4. 优点：速度快，时间复杂度和空间复杂度都很低

5. 缺点：比较脆弱，可能退化到冒泡,当每轮排序总是使左边1个数右边其他数的时候。

6. 代码描述

    //切分函数
    private static int partition(Comparable[] a, int lo, int hi) {
        Comparable v = a[lo];
        int i = lo, j = hi;//i,j分别是左部分指针，右部分指针
        while(true) {
            //左边要找一个比他大的，否则一直找知道i指针到终点hi
            while(i<=hi) 
                if(cmp(a[++i] , v) <= 0); else break;    
                
            //右边要找一个比他小的，否则一直找到j指针到起点lo
            while(j>lo) 
                if(cmp(a[j] , v) >= 0) j--; else break;
                
            //如果ij指针相遇  则说明已经找到a[lo]的位置，
            if(i>=j) break;//这里等号应该取不到因为上面设置的是严格大和严格小，不加等号也 是对的
            exch(a , i , j);//交换位置，把不正确的位置纠正过来，把左边大的与右边小的元素位置互换
        }
        exch(a , lo , j);//最后把第lo个元素放到该 放到的地方
        return j;//返回该轮排序的切分点

    }
    
    //递归排序
    private static void qsort(Comparable[] a, int lo, int hi) {
        // TODO Auto-generated method stub
        
        if(lo >= hi) return ;
        int mid = partition(a , lo, hi);
        qsort(a , lo, mid-1);
        qsort(a,  mid+1, hi);
    }
    //快速排序启动函数
    public static void quickSort(Comparable[] a) {
        
        qsort( a, 0, a.length - 1);
    }

【拓展】三向切分的快速排序

（1）当数组中存在大量相同关键字的元素时，快速排序对其处理的性能损失在大量切分再排序，一个有效的处理方法是使用三向切分的快速排序。

（2）主要思想:每轮排序时，将lo到hi的元素分割成三个部分使得[lo, lt - 1] < V = [lt , gt] < [gt + 1, hi] ,避免对重复元素段进行再排序

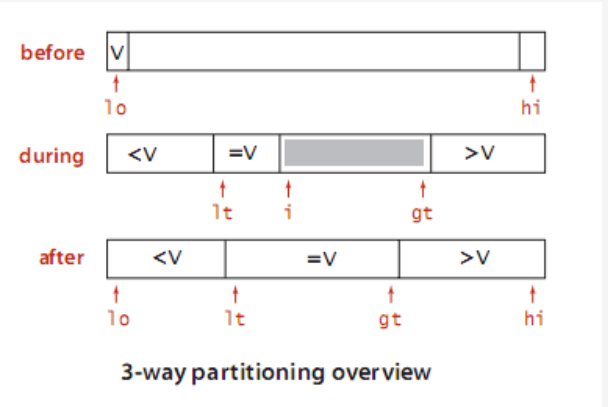
（3）三向切分快排代码描述

    //三向切分快速排序
    public static void qsort3(Comparable[] a, int lo, int hi) {
        if(lo >= hi) return ;
        //lo lt gt hi四个指针 
        //事实上，从lt一开始指向关键字a[lo]，lt就一直指向的值是V，并且lt指的是        
        //第一个V值，它存的其实是左边界
        //排好序后lt ~ gt都是V值
        int lt = lo, i = lo+1 , gt = hi;
        Comparable v = a[lo];
        while(i <= gt ) {
            int re = cmp(a[i] , v);
            if(re < 0) exch(a , i++ ,lt++);
            else if( re > 0) exch(a , i, gt--);
            else i++;
        }
        //只需要再排不等于V的两个部分
        qsort3(a , lo, lt - 1);
        qsort3(a , gt+1 , hi);
    }

六、优先队列（基于数组和堆）

1. 作用：优先队列使得队列首部元素永远是最大值（最小值），并且只能在队首操作（要么查看队首元素要么弹出队首元素），

可以新插入元素并将其插入合适位置使得结构还是优先队列。适用于构造动态变化的优先级结构。

2. 什么是堆？

（1）这里只介绍二叉堆。任意K叉堆可以类比得出。以下简称二叉堆为堆。

（2）二叉堆是一组按照完全二叉树的结构排列的元素，其特点是，如果某一结点在数组中标号为k并且有孩子结点，那么其孩子结点标号是2k, 2k+1(如果有有孩子的话)，

且满足，a[k] >= max(a[2k] , a[2k+1]) 这样的二叉堆叫大根堆，同理有小根堆。

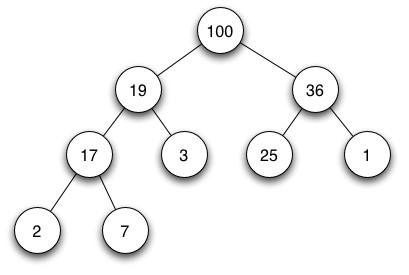
（3）二叉堆中调整元素结构保持大根堆的特性的核心操作有两个，上浮和下沉，都是为了保持结构为堆

//上浮第K号元素
    public void swim(int k) {
        //当前位置是k，则父节点位置为k/2
        while(k > 1 && less(k >> 1, k)) {
            exch(k >> 1, k);//交换二者位置
            k = k >> 1;//继续检验，设置当前位置为父节点位置
        }
    }
    //下沉第K号元素
    public void sink(int k) {
        while(2*k < N) { 
            //检验当前结点是否是大于左右孩子结点
            int j = 2*k;//j指针指向左右孩子中较大的一个
            if(less(j , j+1)) j++;
            //如果当前结点比左右孩子中较大的一个小则交换，父节点下沉
            if(less(k , j)) {
                exch(k , j);
                k = j;
            }
            else {
                break;
            }
        }
    }

3.完整的数据结构如下代码所示

package data_structure;

import java.util.Random;

/*优先队列*/
public class MaxPQ <Key extends Comparable<Key>>{
    
    private Key[] pq;//容器 数组
    private int N;//末尾指针, N=0不指向元素
    private int max;
    //构造函数
    public MaxPQ(int maxN){
        pq = (Key[]) new Comparable[maxN + 1];
        N = 0;
        max = maxN + 1;
    }
    
    //判断空
    public boolean isEmpty() {
        return N == 0;
    }
    
    //返回大小
    public int size() {
        return N;
    }
    
    //插入操作
    public void insert(Key x) {
        //TODO 如果当前size已经超过分配的容量则追加空间
        if(N + 1 >= max) {
            Key[] temp = (Key[]) new Comparable[max * 3 / 2];
            max = max * 3 / 2;
            System.arraycopy(pq, 0, temp, 0, N+1);
            for(int i=1; i<=N; i++)    System.out.print(pq[i].toString() + " ");
            System.out.println();
            pq = temp;//pq重新指向temp
            temp = null;//销毁temp
        }
        
        pq[++N] = x;//先将元素插到末尾，再通过上浮调整结构
        if(pq[N] == null) System.out.println(123);
        swim(N);
        
    }
    
    //删除操作 
    public boolean delMax() {
        //如果当前队列已经空了则返回失败
        if(N == 0) return false;
        //先把顶头元素与末尾元素互换
        exch(1 , N);
        //然后把末尾元素删掉
        N--;
        pq[N+1] = null;//释放空间
        //再调整顶头元素位置
        sink(1);
        return true;
    }
    
    public boolean less(int i, int j) {
        if(pq[i] == null) System.out.println(123);
        return pq[i].compareTo(pq[j]) < 0;
    }
    public void exch(int i, int j) {
        Key t = pq[i]; pq[i] = pq[j]; pq[j] = t;
    }
    //上浮元素
    public void swim(int k) {
        //当前位置是k，则父节点位置为k/2
        while(k > 1 && less(k >> 1, k)) {
            exch(k >> 1, k);//交换二者位置
            k = k >> 1;//继续检验，设置当前位置为父节点位置
        }
    }
    
    public void sink(int k) {
        while(2*k < N) { 
            //检验当前结点是否是大于左右孩子结点
            int j = 2*k;//j指针指向左右孩子中较大的一个
            if(less(j , j+1)) j++;
            //如果当前结点比左右孩子中较大的一个小则交换，父节点下沉
            if(less(k , j)) {
                exch(k , j);
                k = j;
            }
            else {
                break;
            }
        }
    }
    public Key top() {
        return pq[1];
    }
    
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        MaxPQ mpq = new MaxPQ<Integer>(10);
        Random r = new Random();
        for(int i=0; i<100; i++) {
            Integer t = new Integer(r.nextInt(1000));
            mpq.insert(t);
            System.out.println(mpq.top().toString());
        }
    }

}

View Code

【拓展】基于大根堆和sink操作的堆排序

（1）首先给定一个乱序数组，长度为N，将其构造成一个大根堆。

（2）构造方法是，对前N/2号元素逆序（即N/2 N/2 - 1 N/2 - 2 .... 1 ）做sink操作，其实就是最底下一层元素不动，逐级向上构造局部大根堆，使得整体成为大根堆。

（3）得到一个大根堆之后，首项即为最大元素，它的位置理应在最后面，所以将其a[1] 与 a[N]交换，并且使a[1] ~ a[N--]的元素保持为大根堆，只需要对新首项做sink操作即可。

这样操作N次之后，每次得到一个仅次于之前元素的最大值排在后面，相当于是选择排序，这样就能使数组整体有序啦。

（4）时间复杂度：N/2 * log(N) + N*log(N) ，整体为O（Nlog(N)）

（5）代码实现

//堆排序 ， 注意数组a从下标1开始，0号元素没有用
    public static void heapSort(Comparable[] a) {
        int N = a.length - 1;//N是最后一个元素下标
        for(int k = N/2; k>0; k--) {
            sink(a , k, N);
        }
        while(N > 1) {
            exch(a , 1, N--);
            sink(a , 1, N);
        }    
    }
    //一定要注意第三个参数N是当前选定的最后一个位置， 并不一直是数组末尾元素
    private static void sink(Comparable[] a, int k, int N) {

        while(2*k <= N) {
            int j = 2*k;
            if(j < N && cmp(a[j] , a[j+1]) < 0) {
                j++;
            }
            if(cmp(a[k] , a[j]) >= 0) {
                break;
            }
            exch(a , k , j);
            k = j;
        }
    }

---恢复内容结束---

查看全文

相关阅读:
第二周总结
 个人总结
 软件设计模式7
软件设计模式6
软件设计模式5
软件设计模式4
软件设计模式3
软件设计模式2
软件设计模式1
软件构造2

原文地址：https://www.cnblogs.com/czsharecode/p/10531032.html

热门文章
python 学习二
 暑期学习（二）
第十二周总结
 第十周总结
 第九周总结
 第八周总结
 第七周总结
 第五周总结
 第四周总结
 第三周总结