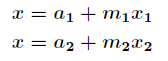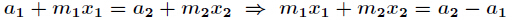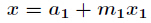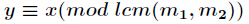中国剩余定理

【定理概述】

　　中国剩余定理（孙子定理）是中国古代求解一次同余式组的方法。是数论中一个重要定理。一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

 

【求逆元】

逆元的含义：模p意义下，1个数a如果有逆元x，那么除以a相当于乘以x。ax≡1(mod p)。

一个数有逆元的充分必要条件是gcd(a,p)=1，此时逆元唯一存在，注意这里的唯一是指在群中唯一 。

其实如果求出一个逆元x0，那么x0 + p*k都会满足上面的等式，但是我只取p内的正整数x0.

 【证明】 由ax≡1(mod p)等价于这样一个方程

a*x + p*y = 1 ，或者说这个方程x有解的话x必然满足 ax≡1(mod p)

这个方程什么时候有解呢？很显然，当gcd(a,p) | 1时有解，所以gcd(a,p)只能是1，即a,p互质，证明完毕。

由此还可以得到一个结论，如果要求逆元，可以用扩展欧几里得求一组解（x,y），再求出x的最小正整数（x+p）%p,

x就是a的唯一逆元。

方法1：费马小定理求逆元，p是质数，且gcd(a,p)=1

在模为素数p的情况下，有费马小定理 
a^p-1 ≡ 1（mod p） 

则a * a^p-2 ≡ 1（mod p）

所以a的逆元就是a^p-2，用快速幂求即可。

#include<iostream>
using namespace std;

long long gcd(long long a, long long b){
    if(b == 0)    return a;
    return gcd(b , a%b);
}

long long qPow(long long a ,long long n,long long mod){
    long long ans = 1;
    //如果n的二进制最后一位是1 结果参与运算 
    //因为如果是0，那么幂运算之后该项是1,1乘任何数还是那个数，对结果不影响
    while(n > 0){
        if(n & 1)  
            ans = (ans* a) % mod;
        a = (a*a) % mod;//底数加倍 
        n >>= 1;//移位 
    }
    return ans;    
}

//
long long invEle(long long a, long long mod){
     
    //如果a 和 模数不互质则必然不存在逆元 
    if(gcd(a,mod) != 1 || mod < 2)    return -1;
    return qPow(a,mod-2,mod);
}

int main(){
    long long a,b;
    int x,y;
    while(cin>>a>>b){
        cout<<invEle(a,b)<<endl;
    }
}

方法2：扩展欧几里得求逆元（高效）

typedef  long long ll;
void extgcd(ll a,ll b,ll& d,ll& x,ll& y){
    if(!b){ d=a; x=1; y=0;}
    else{ extgcd(b,a%b,d,y,x); y-=x*(a/b); }
}
ll inverse(ll a,ll n){
    ll d,x,y;
    extgcd(a,n,d,x,y);
    return d==1?(x+n)%n:-1;
}

方法3：欧拉定理求逆元（很少用到）

模p不是素数的时候需要用到欧拉定理

逆元打表：

typedef  long long ll;
const int N = 1e5 + 5;
int inv[N];
 
void inverse(int n, int p) {
    inv[1] = 1;
    for (int i=2; i<=n; ++i) {
        inv[i] = (ll) (p - p / i) * inv[p%i] % p;
    }
}

【解方程组】

根据定理概述以及解法，得到以下方法

int CRT(int a[],int m[],int n)
{
    int M = 1;
    int ans = 0;
    for(int i=1; i<=n; i++)
        M *= m[i];
    for(int i=1; i<=n; i++)
    {
        int x, y;
        int Mi = M / m[i];
        extend_Euclid(Mi, m[i], x, y);
        ans = (ans + Mi * x * a[i]) % M;
    }
    if(ans < 0) ans += M;
    return ans;
}

【扩展中国剩余定理】

当模数mi两两互质时有以上解法，当模数不确定是否两两互质呢？

摘自博客:https://blog.csdn.net/acdreamers/article/details/8050018

这种情况就采用两两合并的思想，假设要合并如下两个方程

     

那么得到

      

在利用扩展欧几里得算法解出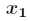的最小正整数解，再带入

      

得到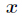后合并为一个方程的结果为

       

这样一直合并下去，最终可以求得同余方程组的解。

#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
const int N = 1005;
LL a[N], m[N];
LL gcd(LL a,LL b)
{
    return b? gcd(b, a % b) : a;
}
void extend_Euclid(LL a, LL b, LL &x, LL &y)
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return;
    }
    extend_Euclid(b, a % b, x, y);
    LL tmp = x;
    x = y;
    y = tmp - (a / b) * y;
}
LL Inv(LL a, LL b)
{
    LL d = gcd(a, b);
    if(d != 1) return -1;
    LL x, y;
    extend_Euclid(a, b, x, y);
    return (x % b + b) % b;
}
bool merge(LL a1, LL m1, LL a2, LL m2, LL &a3, LL &m3)
{
    LL d = gcd(m1, m2);
    LL c = a2 - a1;
    if(c % d) return false;
    c = (c % m2 + m2) % m2;
    m1 /= d;
    m2 /= d;
    c /= d;
    c *= Inv(m1, m2);
    c %= m2;
    c *= m1 * d;
    c += a1;
    m3 = m1 * m2 * d;
    a3 = (c % m3 + m3) % m3;
    return true;
}
LL CRT(LL a[], LL m[], int n)
{
    LL a1 = a[1];
    LL m1 = m[1];
    for(int i=2; i<=n; i++)
    {
        LL a2 = a[i];
        LL m2 = m[i];
        LL m3, a3;
        if(!merge(a1, m1, a2, m2, a3, m3))
            return -1;
        a1 = a3;
        m1 = m3;
    }
    return (a1 % m1 + m1) % m1;
}
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=1; i<=n; i++)
            scanf("%I64d%I64d",&m[i], &a[i]);
        LL ans = CRT(a, m, n);
        printf("%I64d
",ans);
    }
    return 0;
}