爬楼梯算法，LeetCode（70）

问题：假设一个楼梯有n个台阶，一次只能上1个或者2个台阶，请问一共有多少种方式来爬n个台阶。

解答：首先用最笨的方式来发现答案的规律。

　　（1）只有一个台阶，n=1，结果只有一种 result=1；   {1}

　　（2）有两个台阶，n=2，可知结果result=2；   {1+1} ,  {2}

　　（3）当 n=3时，result=3，  {1+1+1},  {1+2},  {2+1}

　　（4）n=4时，result=5；  {1+1+1+1+1},  {1+2+1},  {1+1+2},  {2+1+1},  {2+2}

　　（5）n=5时，result=8；

规律如图：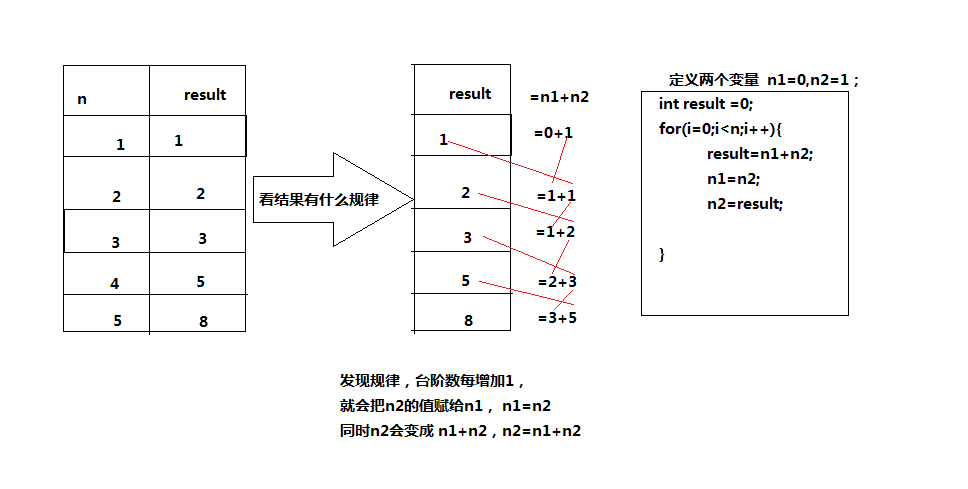

通过分析可知，结果result=n1+n2，台阶数n在变化，n1,n2的值也在不断变化，但是始终有result=n1+n2;  代码如下：

public class Solution {
　　public int climbStairs(int n) {

　　　　int n1 = 0;
　　　　int n2 = 1;
　　　　int result = 0;
　　　　for (int i = 0; i < n; i++) {
　　　　　　result = n1 + n2;
　　　　　　n1 = n2;
　　　　　　n2 = result;
　　　　}　　
　　　　return result;
　　}
}