一、分类
当下主流的编程方法大体分为三类
1. 面向过程
2. 函数式
3. 面向对象
二、函数式编程:函数式 = 编程语言定义的函数 + 数学意义的函数
特征:1. 不可变数据
2. 第一类对象
3. 尾调用优化(尾递归)
例一、不可变:不用变量保存状态,不修改变量
#非函数式
a = 1
def test1():
global a
a += 1
return a
b = test1()
print(b)
#函数式
n = 1
def test2(n):
return n + 1
print(test2(2))
print(n)例
例二、第一类对象:函数即变量
1. 函数名可以当作参数传递
2. 返回值可以是函数名
①
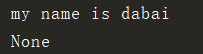
def foo(n):
print(n)
def bar(name):
print('my name is %s'%name)
foo(bar('dabai'))
②
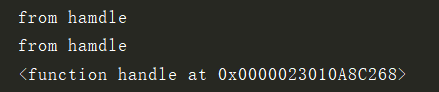
def handle():
print('from hamdle')
return handle
h = handle()
h()
print(h) #打印handle的内存地址
③
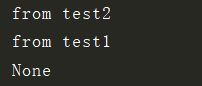
def test1():
print('from test1')
def test2():
print('from test2')
return test1() #return了test1的返回值
a = test2()
print(a)
三、尾调用优化
尾调用的关键就在于是在函数的最后一步去调用别的函数,那么在最后一步调用有何好处,根据函数即变量的定义,定义a 函数,a 内调用函数b,b内调用函数c,在内存中会形成一个调用记录,又称调用帧(call frame),用于保存调用位置和内部变量等信息,即a-->b-->c,直到c返回结果给b,c的调用记录才会消失,b返回给a,b的调用记录消失,a返回结果,a的调用记录消失,所有的调用记录都是先进后出,形成一个调用栈(call stack)
尾调用由于是函数的最后一步操作,所以不需要保留外层函数的调用记录,因为调用位置、内部变量等信息都不会再用到了,只要直接用内层函数的调用记录,取代外层函数的调用记录就可以了。
def bar(n):
return n
def foo(x):
return bar(x)
print(foo(3))
#foo(3)就等于bar(3),也就是说,foo在最后一步调用了bar,然后foo的调用记录就清除了,
剩下得就是bar自己得事情了,所有内存里永远只保留一个调用记录
#函数bar在foo内为非尾调用
def bar(n):
return n
def foo(x):
y = bar(x)
return y
a = foo(3)
print(a)
#函数bar在foo内为非尾调用
def bar(n):
return n
def foo(x):
return bar(x) + 1
a = foo(3)
print(a)
由递归转化为尾递归:
下面代码是一个阶乘函数,计算n的阶层,最多需要保留n个调用记录
def fact(n):
if n == 1:
return n
return n * fact(n - 1)
print(fact(5))
#如果改为尾递归,只保留一个记录
def fact(n, m):
if n == 1:
return m
return fact(n - 1 , n * m)
print(fact(5, 1))