浙江工业大学校赛 画图游戏 BugZhu抽抽抽！！

BugZhu抽抽抽！！

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 695    Accepted Submission(s): 253

Problem Description

当前正火的一款手游阴阳师又出新式神了，BugZhu十分想要获得新出的式神，所以他决定花光所有的积蓄来抽抽抽！BugZhu经过长时间的研究后发现通过画三角外接圆能够提高获得该式神的概率，即如下图所示的图形：



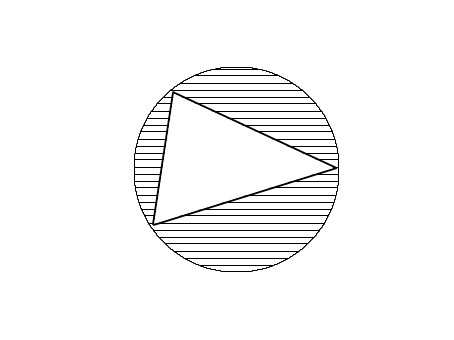
高超的数学天分给予了BugZhu神一般的洞察力，BugZhu还发现当图中阴影部分的面积处在[l,r]之间时，他能够获得最高的概率。BugZhu现在画好了符，他能不能获得最高概率呢？

 

Input

不超过100组数据
每组数据第一行给出l和r(l,r均在double范围内)。
接下来3行，给出所画三角形三个顶点的坐标xi,yi(|xi|,|yi|<=1000)

 

Output

每组数组输出一个YES或NO表示能不能获得最高概率

 

Sample Input

1 5
0.0000 1.0000
-1.0000 0.0000
1.0000 0.0000
3 5
0.0000 1.0000
-1.0000 0.0000
1.0000 0.0000

 

Sample Output

YES
NO
#include <algorithm>
#include <string.h>
#include <stdio.h>
#include <string>
#include <vector>
#include <math.h>
#include <queue>
#include <stack>
#include <map>
#include <set>
using namespace std;
#define _inf 0x3f3f3f3f
#define pi 2 * asin(1.0)

double n, m;
double a[3];
double b[3][2];
double s1, s2, s;
double p, r;

int main()
{
    int i;
    while(~scanf("%lf %lf", &n, &m))
    {
        for(i = 0; i < 3; i++)
        {
            scanf("%lf %lf", &b[i][0], &b[i][1]);
        }
        for(i = 0; i < 3; i++)
        {
            a[i] = sqrt((b[i][0] - b[(i + 1) % 3][0]) * (b[i][0] - b[(i + 1) % 3][0]) + (b[i][1] - b[(i + 1) % 3][1]) * (b[i][1] - b[(i + 1) % 3][1]));
        }
        p = (a[0] + a[1] + a[2]) / 2;
        s1 = sqrt(p * (p - a[0]) * (p - a[1]) * (p - a[2]));
        r = a[0] * a[1] * a[2] / s1 / 4;
        s2 = r * r * pi;
        s = s2 - s1;
        if(s < n || s > m)
            printf("NO
");
        else
            printf("YES
");
    }
    return 0;
}