1、主要内容
上一讲中使用对偶形式的支持向量机将原始的与数据的维度d有关逐步转化到了只有数据输入规模N有关,但是在最后计算对偶形式的Q矩阵时依然还是使用到了数据的维度d,因此还不算时真正的解决了这个问题。

那么有什么方法?

2、对偶形式的不足
上节课中将d转换成与d无关只是做了一半,还没有真正的把d消除:

在计算Q矩阵时,由于Zn,Zm的存在,依然是和维度d有关系,此处就是解决该问题的瓶颈。
如何解决该瓶颈,找到一个更好的计算方法?
注意到Zn和Zm由一下变换得到:
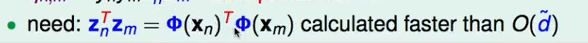
先对原始的x做转换然后再内积,那么转换过程对于d维的数据必然需要O(d)的时间,然后做内积也需要O(d)的时间,因此能不能找到一种种方法简化这个过程?
以2次转换为例:

转换后包括原有的1次项和2次项,那么计算
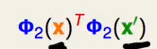
最后得到:
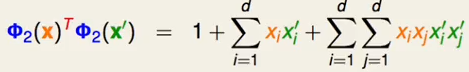
观察上式,最后一项都可以进行整理i和j相关项放到一起:

最后可以得到:
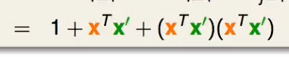
这样的话,先计算出来内积,然后使用这个内积在常数时间内就可以完成转化,那么在这个例子中比原来计算要快。
一如kernel核函数的概念:

kernel核函数集成了内积然后使用内积进行数据的特征变换,达到快速计算的目的,就包括了特征转化和内积这两个步骤;
3、kernel核函数的使用

使用核函数替换Z变换的内积;


4、多项式kernel核函数
上面讲了一个二次多项式的kernel核函数:
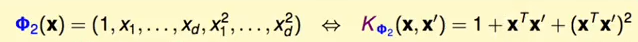
那么对这个kernel 核函数进行加上常数进行放缩,如果转换函数每个一次项都乘上一个√2的话,那么kernel核函数变成:
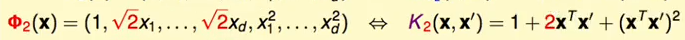
同理:
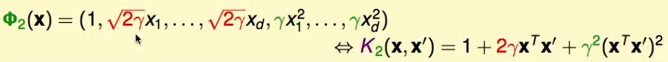
综上可以知道:

上面两种不同的2次kernel对与SVM来说:
就特征转换的结果是相同的,只是放缩了特征值;
但是在计算最终的内积不同就表示向量的距离不一样,因此会影响到SVM最后的结果;
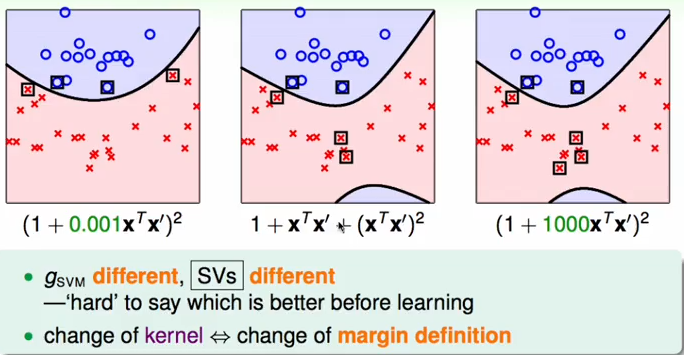
因此改变核函数也就改变了支持向量得到的最终的模型也不相同;因此需要对kernel进行选择达到最好的效果。再次基础上可以进行一般化就是可以进行推广:
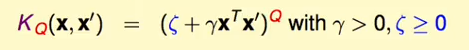
通过多项式的kernel可以高效的进行特征的高次转换而不用考虑数据特征的维度的影响,使用不同的γ和ς来表示不同的多项式kernel核函数:

使用核函数的SVM就被称为多项式SVM:

对一般化进行特殊化得到linear kernel:
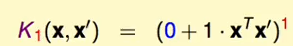
5、高斯核函数
多项式kernel可以将有限维的特征转换进行简化,那么在无限维时怎么办?可以引入高斯核函数;
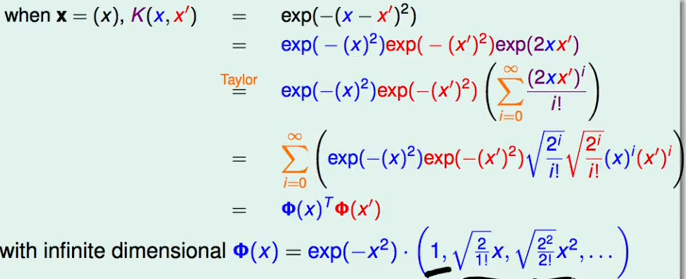
高斯核函数的SVM就是以支持向量为中心的高斯函数的线性组合。

6、不同的kernel的好坏
(1) 线性kernel

好处:
简单,优先尝试,只有结果不好时才尝试其他的kernel
不涉及到复杂的特征转换,可以使用专用的QP解决算法解决
得出的结果容易解释,容易看出不同的支持向量根据其权重对模型的贡献

坏处:
只有数据在线性可分时才可以使用,但是数据不总是线性可分的;

总之。linear kernel值得优先尝试,其他的可以在此基础上进行修改。
(2) 多项式kernel核函数
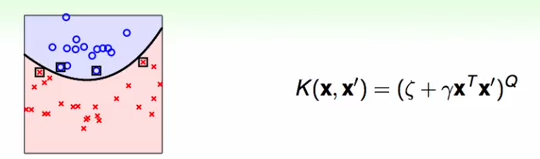
好处:
linear 不行时可以使用多项式,比linear的限制少点
可以认为控制转换的次数Q

坏处:
当Q比较大时计算也很困难;
参数选择比较困难,有三个参数可以选择:

总之,如果使用Q需要小点;
(3) 高斯核函数
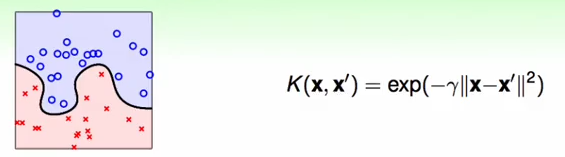
好处:

坏处:

最常用的核函数:

7、其他的kernel

kernel成立的条件:

1、对称
2、矩阵K是一个半正定的;

8、总结
