0.矩阵表示一种变换,把它看成一列一列的列向量,矩阵变换相当于点不动,基变换,基坐标系变为矩阵的这些列向量。
1.相似矩阵,本质上还是同一个变换,坐标系换了,在坐标系a下的矩阵A,等同于坐标系b下的矩阵B。
P-1AP = B

2.特征值的求法 Ax =lmda x 特征值,特征向量,我们把一个矩阵A找到他的相似矩阵B,B是一个对角矩阵,
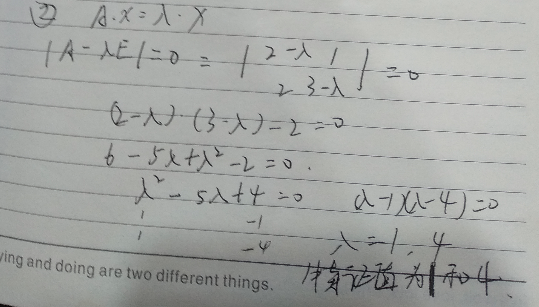
半正定矩阵 所有特征值均不小于0
正定矩阵 所有特征值均大于0
可逆矩阵 也称非奇异矩阵
奇异 表示性质不好(容易丢失数据),相当于行列式为零的矩阵
正交矩阵 AT * A=E AT =A-1 转置矩阵 == 逆矩阵
A的各行各列 都是单位向量,且两两正交 |A| =1

