牛顿运动方程基础就是牛二运动定律
\[{\bf F} = {\bf M}\ddot{\bf x}
\]
将此二阶方程写为两个一阶方程组
\[\begin{cases}
\dot{\bf v} &= {\bf FM}^{-1} \\
\dot{\bf x} &= \bf v
\end{cases}
\]
其隐式表达式为
\[\begin{cases}
{\bf v}^{t+h} &= {\bf v}^t + {\bf F}^{t+h}{\bf M}^{-1}h \\
{\bf x}^{t+h} &= {\bf x}^t + {\bf v}^{t+h}h
\end{cases}
\]
利用泰勒级数对\(\bf F(x,v)\)进行一阶展开,
\[\begin{align}
{\bf F}^{t+h} &= {\bf F}^t + \frac{{\bf F}'}{1!}({\bf x}^{t+h}-{\bf x}^t,{\bf v}^{t+h}-{\bf v}^t) \\
&= {\bf F}^t + \frac{\partial \bf F}{\partial \bf x}\Delta {\bf x} + \frac{\partial \bf F}{\partial \bf v}\Delta {\bf v}
\end{align}
\]
其中\(\Delta {\bf x} = {\bf x}^{t+h} - {\bf x}^{t}\), \(\Delta {\bf v} = {\bf v}^{t+h} - {\bf v}^t\)
带入上面的方程组,整理,可以得到下面的欧拉隐式方程
\[({\bf M} - \frac{\partial{\bf F}}{\partial \bf v}h - \frac{\partial{\bf F}}{\partial \bf x}h^2)\Delta {\bf v} = ({\bf F} + \frac{\partial \bf F}{\partial \bf x}{\bf v}h)h
\]
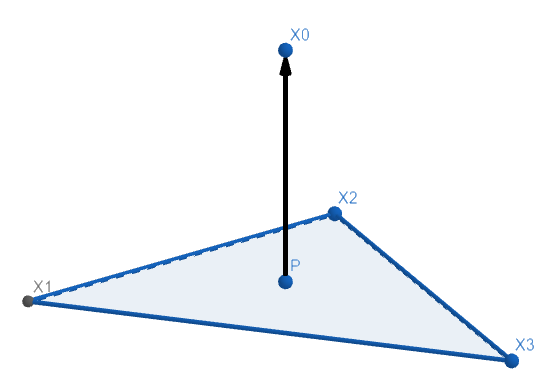
(配图的面的顺序,弄反了,右手系下X2与X3的位置应该换一下。。。)
在布料系统中,很多受力与速度\(\bf v\)无关,所以问题通常集中在求解\(\frac{\partial{\bf F}}{\partial \bf x}\)上。假设有如下4个点\({X_0,X_1,X_2,X_3}\),其中\(X_1\),\(X_2\),\(X_3\)组成三角形,\(X_0\)在三角形上的投影为\(P = \alpha{_1}X_1+\alpha{_2}X_2 + \alpha{_3}X_3\)。它们的受力为斥力,有
\[\begin{aligned}
F_{X_0}&= f_{\tt stiff} \cdot (X_0 - P) = f \cdot (X_0 - (\alpha_1X_1+\alpha_2X_2+\alpha_3X_3))\\
F_{X_1}&= -\alpha_1 F_{X_0} \\
F_{X_2}&= -\alpha_2 F_{X_0} \\
F_{X_3}&= -\alpha_3 F_{X_0}
\end{aligned}
\]
,\(f_{\tt stiff}\)为系数。
那么,在求\(\frac{\partial{\bf F}}{\partial \bf x}\)的时候,就要需要对\(F_{X_0}\),\(F_{X_1}\),\(F_{X_2}\),\(F_{X_3}\),分别对\({X_0,X_1,X_2,X_3}\)进行求解。
对于点\(X_0\)来说,
\[\begin{aligned}
\frac{\partial F}{\partial X_0} &= (\frac{\partial F_{X_0}}{\partial X_0}, \frac{\partial F_{X_1}}{\partial X_0},\frac{\partial F_{X_2}}{\partial X_0},\frac{\partial F_{X_3}}{\partial X_0}) \\
&= (\frac{\partial F_{X_0}}{\partial X_0}, -\alpha_1\frac{\partial F_{X_0}}{\partial X_0},-\alpha_2\frac{\partial F_{X_0}}{\partial X_0}, -\alpha_3\frac{\partial F_{X_0}}{\partial X_0})
\end{aligned}
\]
对其他三个点,情形类似。
\[\begin{aligned}
\frac{\partial F}{\partial X_1} &= (\frac{\partial F_{X_0}}{\partial X_1}, \frac{\partial F_{X_1}}{\partial X_1},\frac{\partial F_{X_2}}{\partial X_1},\frac{\partial F_{X_3}}{\partial X_1}) \\
&= (\frac{\partial F_{X_0}}{\partial X_1}, -\alpha_1\frac{\partial F_{X_0}}{\partial X_1},-\alpha_2\frac{\partial F_{X_0}}{\partial X_1}, -\alpha_3\frac{\partial F_{X_0}}{\partial X_1}) \\
\\
\frac{\partial F}{\partial X_2} &= (\frac{\partial F_{X_0}}{\partial X_2},- \alpha_1\frac{\partial F_{X_0}}{\partial X_2},-\alpha_2\frac{\partial F_{X_0}}{\partial X_2}, -\alpha_3\frac{\partial F_{X_0}}{\partial X_2}) \\
\\
\frac{\partial F}{\partial X_3} &= (\frac{\partial F_{X_0}}{\partial X_3},-\alpha_1\frac{\partial F_{X_0}}{\partial X_3},-\alpha_2\frac{\partial F_{X_0}}{\partial X_3}, -\alpha_3\frac{\partial F_{X_0}}{\partial X_3}) \\
\end{aligned}
\]
至于求\(\frac{\partial F_{X_0}}{\partial X_i}\),按照雅可比公式来求就可以了
\[\frac{\partial{\bf F}}{\partial \bf x} = \begin{bmatrix}
\frac{\partial f_x}{\partial \bf x} \\
\frac{\partial f_y}{\partial \bf x} \\
\frac{\partial f_z}{\partial \bf x}
\end{bmatrix} =
\begin{bmatrix}
\frac{\partial f_x}{\partial {\bf x}_x} \ \frac{\partial f_x}{\partial {\bf x}_y} \ \frac{\partial f_x}{\partial {\bf x}_z} \\
\frac{\partial f_y}{\partial {\bf x}_x} \ \frac{\partial f_y}{\partial {\bf x}_y} \ \frac{\partial f_y}{\partial {\bf x}_z} \\
\frac{\partial f_z}{\partial {\bf x}_x} \ \frac{\partial f_z}{\partial {\bf x}_y} \ \frac{\partial f_z}{\partial {\bf x}_z}
\end{bmatrix}
\]
求解:
\[\begin{aligned}
\frac{\partial F_{X_0}}{\partial X_0} &=
\begin{bmatrix}
&f_{\tt stiff} \ &0 \ &0 \\
&0 \ &f_{\tt stiff} \ &0 \\
&0 \ &0 \ &f_{\tt stiff} \\
\end{bmatrix} \\
\frac{\partial F_{X_0}}{\partial X_1} &= -\alpha_1 \cdot \frac{\partial F_{X_0}}{\partial X_0} \\
\frac{\partial F_{X_0}}{\partial X_2} &= -\alpha_2 \cdot \frac{\partial F_{X_0}}{\partial X_0} \\
\frac{\partial F_{X_0}}{\partial X_3} &= -\alpha_3 \cdot \frac{\partial F_{X_0}}{\partial X_0}
\end{aligned}
\]
以上。
参考文献
忘了出处了……好久以前写的了……