一.排序算法
1.直接插入排序:
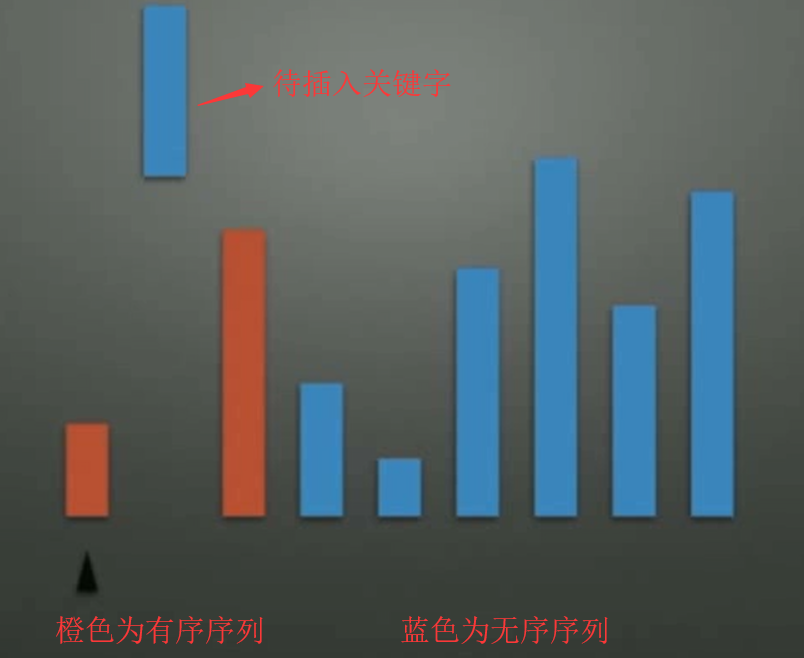
//直接插入排序:
//初始最左边为有序序列,其余为无序序列,一一对比,再把无序的关键字挪动有序对应位置
void insertSort(int arr[],int n) //整型数组,关键字个数
{
int i,j,temp; //下标,temp为暂存待插入的关键字
for(i=1; i < n; ++i) //下标为0的关键字为有序序列,i循环范围1<i<n,外层循环为无序序列,第一个为有序关键字
{
temp = arr[i]; //最大关键字存入辅助常量
j = i-1; //j为有序序列,无序序列的左边一个为有序序列
while (j>=0 && temp<arr[j]) //当有序序列的范围大于0,temp小于j扫描到的关键字,内层循环为有序序列
{
arr[j+1] = arr[j]; //每扫描到关键字往后移动一位
--j; //下标也往前移动一位
}
arr[j+1] = temp; //指示标志落在最后待插入的前一个位置
}
}
2.简单选择排序

//简单选择排序:
//每次找到最小关键字,移动至无序最左边
void selectSort(int arr[],int n)
{
int i,j,k; //下标
int temp;
for(i=0;i < n;++i)
{
k = i; //记录下标
for (j=i+1 ;j < n; ++j)
if (arr[k] > arr[j]) //比较最值
k = j; //把最小值的下标赋值给k
temp = arr[i]; //第一个关键字与最小值对调
arr[i] = arr[k];
arr[k] =temp;
}
}
3.冒泡排序:
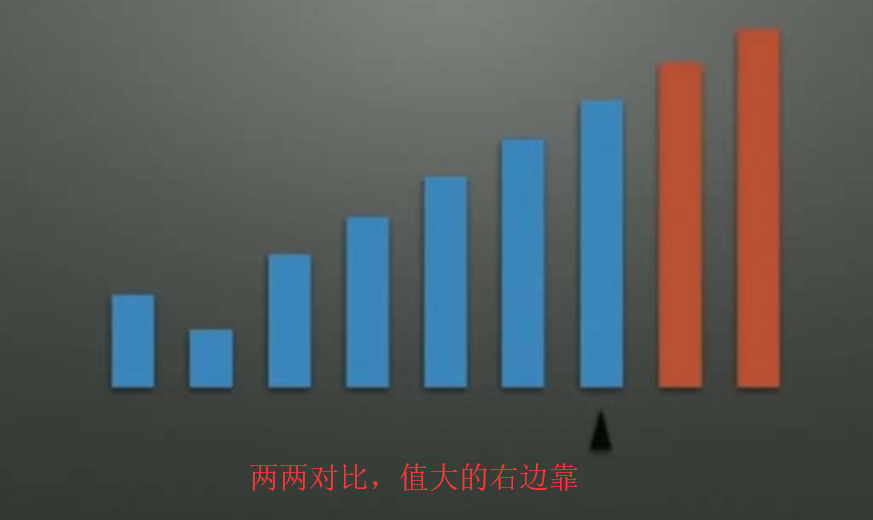
//冒泡排序:
//两两关键字对比,大的关键字移动到右边,一轮循环下来最右边关键字为最大值,后续在无序序列进行多趟操作。
void bubleSort(int arr[],int n) //整型数组,关键字个数
{
int i,j,flag,temp;
for(i=n-1;i >= 1;--i) //无序序列的范围
{
flag = 0;
for (j=1;j<=i;++j) //扫描当前的无序序列,此处为什么没有j=0?下面有arr[j-1] > arr[j]比较,而下标0前面没有数可以比较
if (arr[j-1] > arr[j])
{
temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] =temp;
flag = 1; //有交换,flag变更为1
}
if (flag == 0)
return;
}
}
4.shell排序



//shell排序
//(先将整个待排元素序列切割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,
然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。)
viod shellSort(int arr[],int n)
{
int temp;
for(int gap=n/2;gap>0;gap/=2)
{
for(int i=gap;i<n;++i)
{
temp=arr[i];
int j;
for(j=i;j>=gap && arr[j-gap]>temp;j-=gap) //每个元素与自己组内的数据进行直接插入排序
arr[j]=arr[j-gap];
arr[j]=temp;
}
}
}
5.堆排序
建立大顶堆

插入节点:

删除节点:

//堆排序
//关键字调整函数
void Sift(int arr[],int low,int high) //arr[]中是一棵完全二叉树,所以元素的存储必须从1开始
{
int i=low,j=2*i+1; //arr[j]是arr[i]的左孩子结点
int temp=arr[i]; //temp暂存要调整节点关键字值
while(j<=high)
{
if(j<high && arr[j]<arr[j+1]) //若右孩子较大,则把j指向右孩子
++j; //j变为2*i+2
if(temp<arr[j])
{
arr[i]=arr[j]; //将arr[j]调整到双亲结点的位置上
i=j; //修改i和j的值,以便继续向下调整
j=2*i+1;
}
else
break; //调整结束
}
arr[i]=temp; //被调整结点的中放入最终位置
}
//堆排序函数
viod heapSort(int arr[],int n)
{
int i;
int temp;
for(i=n/2-1;i>=0;--i) //此for循环建立一个大顶堆,i为递减,说明从最后一个分叶节点往前逐个调整
Sift(arr,i,n-1); //存储二叉树的数组;本趟循环要调整的节点下标;堆中最后一个节点下标
for(i=n-1;i>=0;--i) //进行n-1次循环,完成堆排序
{ //以下3句,0位置关键字与当前最大关键字(也就是i位置关键字)交换
temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
Sift(arr,0,i-1); //无序序列的边界[0,被换出的关键字前一个位置]
}
}
6.快速排序
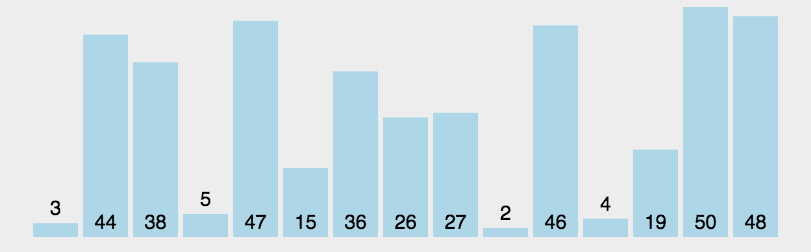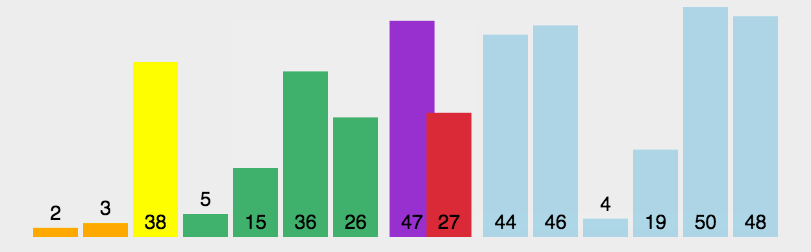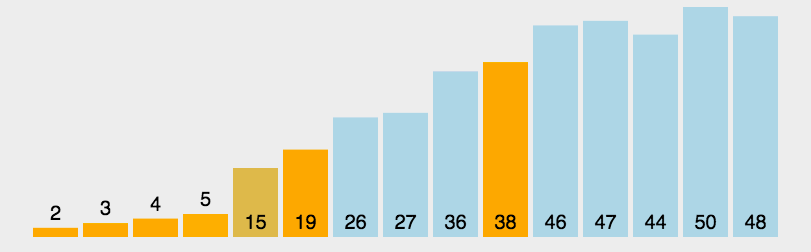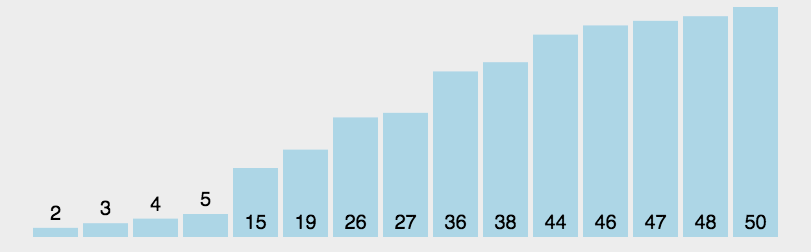
//快速排序
//快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,
则可分别对这两部分记录继续进行排序,以达到整个序列有序。
function quickSort(arr, left, right) {
var len = arr.length,
partitionIndex,
left = typeof left != 'number' ? 0 : left,
right = typeof right != 'number' ? len - 1 : right;
if (left < right) {
partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex-1);
quickSort(arr, partitionIndex+1, right);
}
return arr;
}
function partition(arr, left ,right) { // 分区操作
var pivot = left, // 设定基准值(pivot)
index = pivot + 1;
for (var i = index; i <= right; i++) {
if (arr[i] < arr[pivot]) {
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index - 1);
return index-1;
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
7.归并排序

//归并排序
//将一个数组中的两部分子表归并成一个更长的表(待归并与归并后结果都是在同一个数组当中)
void merge(int arr[],int low,int mid,int high)
{
int i,j,k;
int n1=mid -low+1; //下标为[low,mid]
int n2=high-mid; //下标为[mid+1,high]
int L[n1],R[n2];
for(i=0;i<n1;i++)
L[i]=arr[low+i];
for(j=0;j<n2;j++)
R[j]=arr[mid+1+j];
i=0;
j=0;
k=low;
while(i<n1 && j<n2)
{
if(L[i]<=R[j])
arr[k]=L[i++];
else
arr[k]=R[j++];
k++;
}
while(i<n1)
arr[k++]=L[i++];
while(j<n2)
arr[k++]=R[j++];
}
void mergeSort(int arr[],int low,int mid,int high)
{
if(low<high)
{
int mid=(low+high)/2;
mergeSort(arr,low,mid); //归并排序前半段
mergeSort(a,mid+1,high); //归并排序后半段
merge(A,low,mid,high); //merge()函数:把A数组中low到mid和mid+1到high范围内的两段有序序列归并成一段有序序列
}
}
8.基数排序
初始基数

按个位数-分类与收集


按十位数-分类与收集


按百位数-分类与收集


二.算法复杂度

更多资料,请参考: