数据结构-二叉树遍历

这篇博文主要是研究二叉树遍历的递归与非递归算法，有兴趣的小伙伴可以了解下！

二叉树的递归遍历（深度优先遍历）

先来张图，看看各结点遍历时的情况：

二叉树深度优先遍历总结（分别为第一次，第二次，第三次进入某个结点）：

1. 先序遍历：先访问根结点，然后先序遍历左子树，最后先序遍历右子树；根->左->右
2. 中序遍历：先中序遍历左子树，然后访问根结点，最后中序遍历右子树；左->根->右
3. 后续遍历：先后序遍历左子树，然后后序遍历右子树，最后访问根结点；左->右->根

递归遍历内部有系统栈，其作用：

• 1.保护现场（类似存档）
• 2.恢复现场（类似读档）

 

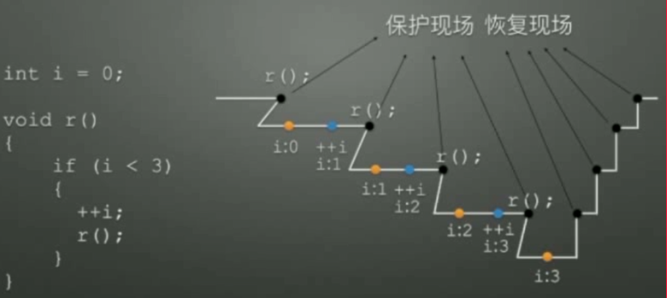
递归遍历代码比较简单，先、中、后序遍历递归代码基本相似，总代码：

void r(BTNode *p)
{
	if (p != NULL)
	{
		//第一次进入-先序
		r(p->lchild);
		//第二次进入-中序
		r(p->rchild);
		//第三次进入-后序
	}
}

先序遍历递归函数：

void r(BTNode *p)
{
	if (p != NULL)
	{
		visit(p);
		r(p->lChild);
		r(p->rChild);
	}
}

二叉树的非递归遍历（深度优先遍历）

须知：非递归需要自定制辅助栈

1.先序遍历非递归:

1).利用辅助栈将根节点入栈，出栈操作，访问该节点，将其右、左孩子分别入栈（每次访问节点后，对其左、右孩子需要做一个检测，为空的孩子无需入栈）
2).左孩子出栈，访问该节点，将其右、左孩子分别入栈，多次操作！
3).直至栈空为止（出栈是在循环之内执行，即使栈空也会执行右左孩子入栈操作）

void preorderNonrecursion(BTNode *bt)
{
	if (bt != NULL)								//根节点是否为空
	{
		BTNode *Stack[maxSize];
		int top = -1;							//创建栈
		BTNode *p = NULL;						//遍历指针
		Stack[++top] = bt;						//节点入栈
		while(top != -1)						//栈不空时循环
		{	
			p = Stack[top--];					//出栈一个元素
			Visit(p);							//访问
			if(p->rChild != NULL)				//右孩子不为空就入栈
				Stack[++top] = p->rChild;
			if(p->lChild != NULL)				//左孩子不为空就入栈
				Stack[++top] = p->lChild;	
		}
	}
}

2.后序遍历非递归：

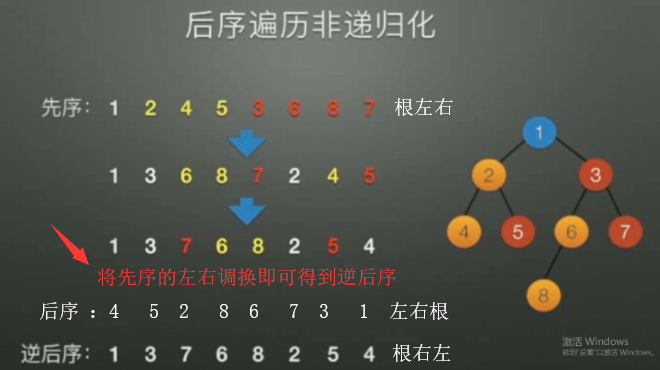
// 先序（根左右），而后序（左右根），将后序逆转为逆后序（根右左），逆后序的左右交换即可成为前序（根左右）
// 在这我们可以使用逆后序（根右左），把逆后序的结果压入一个新栈，出栈就得到后序遍历序列

1).将根节点入辅助栈（栈1），出栈操作，将出栈后的该元素入逆序栈（栈2），将其左、右孩子分别入辅助栈（每次对其左、右孩子需要做一个检测，为空的孩子无需入栈）；
2).右孩子出辅助栈（栈1），将出栈后的该元素入逆序栈（栈2），将其左、右孩子分别入辅助栈（栈1），多次操作；
3).直至辅助栈空为止，出栈是在循环之内执行，即使栈空也会执行左右孩子入栈操作；
4).逆序栈（栈2）中元素逐个出栈并访问

void postorderNonrecursion(BTNode *bt)
{
	if (bt != NULL)								//根节点不为空
	{
		BTNode *Stack1[maxSize];int top1= -1;	//创建栈1（辅助遍历的栈）
		BTNode *Stack2[maxSize];int top2= -1;	//创建栈2（结果逆序的栈）					
		BTNode *p = NULL;						//遍历指针
		Stack1[++top1] = bt;					//节点入栈1
		while(top1 != -1)						//栈不空时循环
		{	
			p = Stack1[top1--];					//栈1出栈一个元素
			Stack2[++top2] = p;					//出栈元素入栈2							
			if(p->lChild != NULL)				//左孩子不为空就入栈
				Stack[++top] = p->lChild;
			if(p->rChild != NULL)				//右孩子不为空就入栈
				Stack[++top] = p->rChild;				
		}
		while(top2 != -1)
		{
			p = Stack2[top2--];					//栈2元素逐个出栈
			Visit(p);							//访问
		}
	}
}

3.中序遍历非递归代码

1).从根节点开始，一直左走，并把途径的左孩子节点入栈；
2).遇到左孩子为空时，栈顶元素出栈，访问该节点，p指向该节点的右孩子；
3).直到栈空或者P为NULL则遍历结束

void inorderNonrecursion(BTNode *bt)
{
	if(bt != NULL)								//树不空
	{
		BTNode *Stack[maxSize];int top = -1;	//创建栈							
		BTNode *p = NULL;						//遍历指针
		p = bt;									//节点入栈1
		while(top != -1 || p != NULL)			//栈不空或者p不空
		{	
			while(p != NULL)
			{
				Stack[++top] = p;				//入栈
				p = p->lChild;					//左走
			}										
			if(top != -1)						
			{
				p = Stack[top--];				//出栈
				Visit(p);						//访问该节点
				p = p->rChild;					//右走
			}			
		}		
	}
}