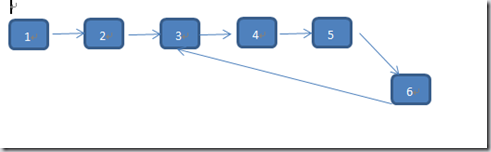
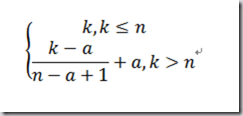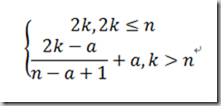C专家编程在附录A2讨论了链表环检测的算法,实现一下,算法一通过设置标志,复杂度O(N),算法二就是所谓的追赶法,算法还是很好理解的,在链表尾部形成的环中,假设两个步伐不一致的的人在绕圈,总有一个交点,但是要证明该算法的正确性似乎还要费一些精力。
先给出实现:
1: /*
2: Expert C Programming,Chinese Edition
3: How to detect loop in linked list, p274,solution1
4: */
5: int check_loop1(pnode list)
6: {
7: pnode p=list;
8: while(p!=NULL)
9: {
10: if(p->flag==1)
11: {
12: return 1;
13: }
14: else
15: {
16: p->flag=1;
17: }
18: p=p->next;
19: }
20:
21: return 0;
22: }
23:
24: /*
25: Expert C Programming,Chinese Edition
26: How to detect loop in linked list, p274,solution4
27: */
28: int check_loop2(pnode list)
29: {
30: pnode p1=list;
31: pnode p2=list;
32: if(p1==p2->next)
33: {
34: return 1;
35: }
36:
37: while(p1->next!=NULL && p2->next!=NULL)
38: {
39: p1=p1->next;
40: p2=p2->next->next;
41: if(p1==p2)
42: {
43: printf("%d",p1->value);
44: return 1;
45: }
46: }
47:
48: return 0;
49: }
设链表长度为n,出现环点处为a.
要证明在有环链表中,步长为1和2的两个向量移动必有相遇点,也就意味着要解方程。
向量1移动k步之后所在的点应该是:
向量2移动k步之后所在的点应该是:
其中的除法运算应视作求模运算。
显然解方程就是求存在这样的k使得两个向量组有共解。比如如果k=0,则k=2k,意味着在链表第一个节点就开始循环。
如果循环点就是链表尾端,则意味着n=a,于是(2k-a) mod (n-a+1)永远为0,=>a=k,意味着a步之后就能侦测出现环。
如果是其它情况,就意味着要解方程:
k=(2k-a) mod (n-a+1)+a (1)
或者另外一个
(k-a) mod (n-a+1) +a=(2k-a) mod (n-a+1)+a
, (2)
要证明对于任意的n与a,都有整数k存在使得等式成立。
---------------------------------------------
现观察方程(2),等式两边消去a后这是一个典型的同余方程,我们根据同余的定义(这里我参考了Rosen的《离散数学及其应用》中文版p152),要使方程成立,则有且仅有(n-a+1)|(2k-a-k+a),即n-a+1整除k,于是我们知道k的值就是d*(n-a+1),其中d为正整数,且k>=a(这是很明显的,否则步长为1的向量还没走到环点,也意味还没进环呢![]() ),于是我们知道方程(2)必然有解。分析完毕。
),于是我们知道方程(2)必然有解。分析完毕。
再注:第一个向量组中的两个表达式其实都可以用(k-a) mod (n-a+1)+a表示。
复杂度分析:
已知k的形式如:k=d*(n-a+1)且k>=a,故两向量第一次相遇时的步长k就取第一个大于a的d*(n-a+1),其步长是线性的,故复杂度可以表示为O(N).
还能再精确一点嘛?能否确定第一个k不小于链表长度呢?因为对比我简单的草稿,所有的结果都暗示可能有这个结论。
如果是死理性派在这里,他们肯定会说这是应该的,假设他们就在这里,现猜测:第一个k应该<=n,为证明猜想,现需要求解不等式n>=d*(n-a+1)>=a即:n+1>d*(n-a+1)>a-1
即:(n+1)/(n-a+1)>d>(a-1)/(n-a+1)
于是需要证明存在这样的正整数d。而域『(a-1)/(n-a+1),(n+1)/(n-a+1)』的长度为(n-a+2)/(n-a+1)显然长度大于1,
于是可知必然存在满足不等式的正整数d。于是
我们就此得知,在n步之内,必然两向量相遇。也意味着步长为1的向量顶多走n步,而别忘了,n是单链表的长度(节点数)。
于是找到环所需要的时间复杂度就是O(N),也即是O(1).
------------------------------------------------------------