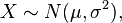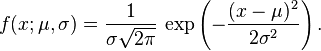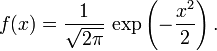正态分布(normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为:
则其概率密度函数为
正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布(见右图中绿色曲线)。
目录 [] [编辑] 概要正态分布是自然科学与行为科学中的定量现象的一个方便模型。各种各样的心理学测试分数和物理现象比如光子 计数都被发现近似地服从正态分布。尽管这些现象的根本原因经常是未知的, 理论上可以证明如果把许多小作用加起来看做一个变量,那么这个变量服从正态分布(在R.N.Bracewell的Fourier transform and its application中可以找到一种简单的证明)。正态分布出现在许多区域统计: 例如, 采样分布均值是近似地正态的,既使被采样的样本总体并不服从正态分布。另外,正态分布信息熵 在所有的已知均值及方差的分布中最大,这使得它作为一种均值以及方差已知的分布的自然选择。正态分布是在统计以及许多统计测试中最广泛应用的一类分布。在概率论, 正态分布是几种连续以及离散分布的极限分布。
[编辑] 历史正态分布最早是棣莫佛在1734年发表的一篇关于二项分布文章中提出的。拉普拉斯在1812年发表的《分析概率论》(Theorie Analytique des Probabilites)中对棣莫佛的结论作了扩展。现在这一结论通常被称为棣莫佛-拉普拉斯定理。
拉普拉斯在误差分析试验中使用了正态分布。勒让德于1805年引入最小二乘法这一重要方法;而高斯则宣称他早在1794年就使用了该方法,并通过假设误差服从正态分布给出了严格的证明。
“钟形曲线”这个名字可以追溯到Jouffret 他在1872年首次提出这个术语"钟形曲面",用来指代二元正态分布(bivariate normal). 正态分布这个名字还被Charles S. Peirce, Francis Galton, Wilhelm Lexis在1875分布独立的使用。这个术语是不幸的,因为它反应和鼓励了一种谬误,即很多概率分布都是正态的。 (请参考下面的"实例")
这个分布被称为“正态”或者“高斯”正好是Stigler名字由来法则的一个例子,这个法则说“没有科学发现是以它最初的发现者命名的”。
[编辑] 正态分布的定义有几种不同的方法用来说明一个随机变量。最直观的方法是概率密度函数,这种方法能够表示随机变量每个取值有多大的可能性。累积分布函数是一种概率上更加清楚的方法,但是非专业人士看起来不直观(请看下边的例子)。还有一些其他的等价方法,例如cumulant、特征函数、动差生成函数以及cumulant-生成函数。这些方法中有一些对于理论工作非常有用,但是不够直观。请参考关于概率分布的讨论。
[编辑] 概率密度函数
正态分布的概率密度函数 均值为 μ 方差 为σ2 (或标准差 σ) 是高斯函数的一个实例:
(请看 指数函数 以及 π.)
如果一个随机变量X 服从这个分布,我们写作 X ~ N(μ,σ2). 如果 μ = 0 并且 σ = 1, 这个分布被称为标准正态分布, 这个分布能够简化为
右边是给出了不同参数的正态分布的函数图。
正态分布中一些值得注意的量: