数据挖掘相关知识

Association Rule（关联规则）

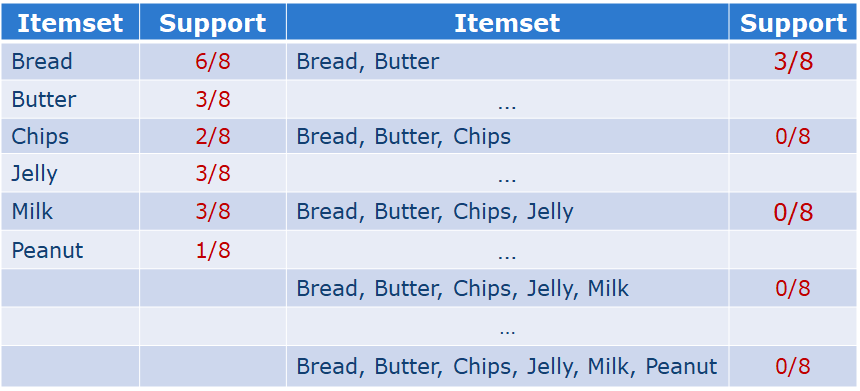
(1)Support of an Itemset(支持项集)

The support of an item (or itemset) X is the percentage of transactions in which that item (or itemset) occurs.项（或项集）X的支持是该项（或项集）发生的事务的百分比。

(2)Support & Confidence of Association Rule(关联规则的支持度与置信度)

The support of an association rule X->Y is the percentage of transactions that contain X and Y.

(包含X和Y的事务百分比)

The confidence of an association rule X->Y is the ratio of the number of transactions that contain {X, Y} to the number of transactions that contain X.

===>（包含x、y的事务数与包含x的事务数的比率）

例：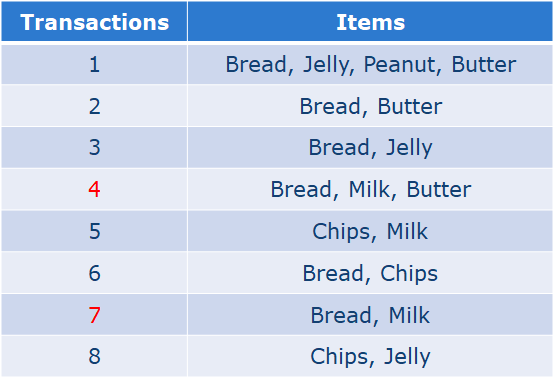    

1、Bread ->Milk

     Support: 2/8

     Confidence: 1/3

2、Milk -> Bread

     Support: 2/8

     Confidence: 2/3

Support and Confidence are bounded by thresholds:Minimum support σ、Minimum confidence Φ；
A frequent (large) itemset is an itemset with support larger than σ.A strong rule is a rule that is frequent and its confidence is higher than Φ.

误区：（1）一个规则很强并不不代表有意义。例：

现在我们有了一个强有力的规则：磁带->DVD。似乎磁带有助于推销DVD，但是，P（DVD）=75%>P（DVD|Tape）,磁带购买者不太可能购买DVD。
置信度很大，但是小于先验概率；

（2）当两个商品出现的概率相差很打时，产生的规则没有意义。

（3）两件事情相关不等于因果关系。Association ≠ Causality。

The Apriori Method:

Key ideas:(1)A subset of a frequent itemset must be frequent.     eg:{Milk, Bread, Coke} is frequent  -> {Milk, Coke} is frequent;

                 (2)The supersets of any infrequent itemset cannot be frequent.    eg:{Battery} is infrequent -> {Milk, Battery} is infrequent.

一般程序： 

                 

（扫描数据库一次，看哪些是频繁的，再使用频繁项集来生成侯选项集，尽量避免去生成不频繁的候选项集，缺点：要多次扫描数据库）

Aprior 算法:

C_k: Candidate itemset of size k（长度为k的候选集）
L_k: Frequent itemset of size k（长度为k的频繁项集）

对数据集中的每条记录transaction

对每个候选项集candidate：

　　检查一下candidate是否是transaction的子集：

　　如果是，则增加candidate的计数值

对每个候选项集：

如果其支持度不低于最小值，则保留该项集

返回所有的频繁项集列表