1. list 画点
>>> from plotting import plot >>> L = [[2, 2], [3, 2], [1.75, 1], [2, 1], [2.25, 1], [2.5, 1], [2.75, 1], [3, 1], [3.25, 1]] >>> plot(L)
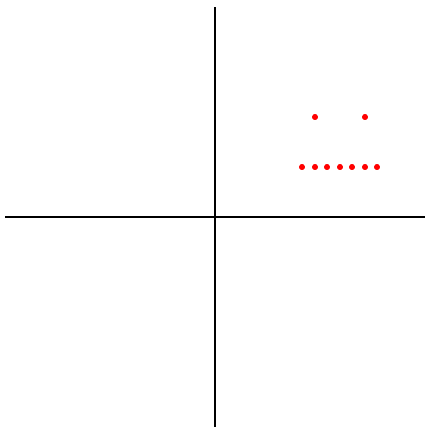
2. 缩放
alpha × vec = [alpha × elem for elem in vec]
>>> def scalar_vector_mult(alpha, v): return [alpha*x for x in v] ... >>> v = [3, 2] >>> plot([scalar_vector_mult(i/10., v) for i in range(11)], 5)
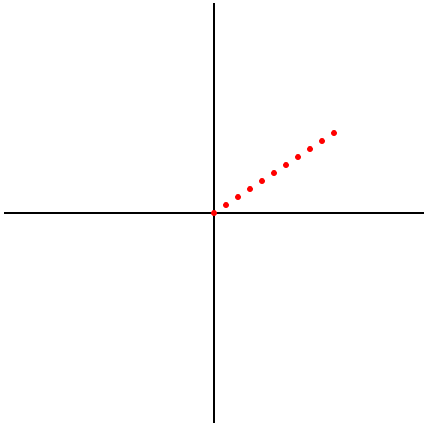
3. 仿射:加乘组合

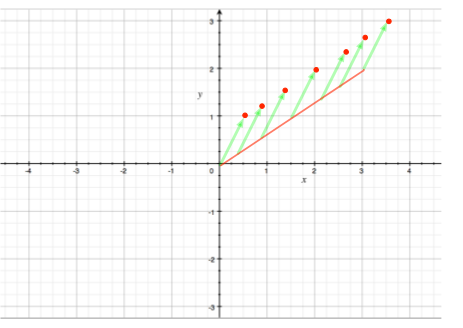
得到从 [0, 0] + [0.5,1] 开始到 [3, 2] + [0.5, 1] 结束的线段。 这种表示方法对 端点来说不具有对称性。如何转换?

现在对于端点来说就具有对称性了。通过这两个端点的直线包含了两个端点对应向量的 仿射集合。
4. GF(2) 加密
a) 要将期中考试的一份试卷交给两个助教,为了防止某一个助教舞弊,发给两个人的加密后的数据必须 合二为一才能进行解密,具体过程如下:
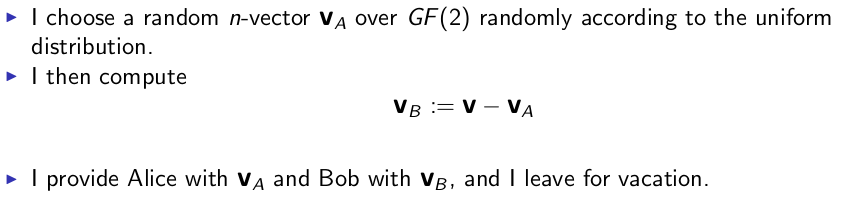
b) 电脑认证登陆——黑客可能窃听,不适合直接传输用户密码。解决方案:电脑给出一串二进制问题,用户掌握一串二进制密码,在 GF(2) 上点乘(先乘再加),得到输出。

黑客窃听到数个电脑的问题 alpha 和用户计算后的结果 beta,需要知道用户的密码,需要解方程:
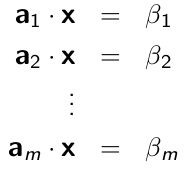
5. 点乘
两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:
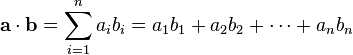
在欧几里得空间中,点积可以直观理解为:

用公式可以表示为:

直观地说,就是向量 A 在向量 B 方向的投影,再乘以 B 的长度。如果将 B 的长度标准化,那么点乘就可以表示两个向量之间的相似性了。比如在一段长音频中匹配一段短音频,可以把短的音频逐个往后移动,每次移动进行一次点乘计算,值越大,相似性越大,DFT 和 DCT 变换都是基于这种操作求不同频域的组分大小的。
编程待续:点乘——用字典类型编写向量类
用向量类解三角线性方程组的根