声明
-
之前虽然听过压缩感知和稀疏表示,实际上昨天才正式着手开始了解,纯属新手,如有错误,敬请指出,共同进步。
-
主要学习资料是 Coursera 上 Duke 大学的公开课——Image and video processing, by Pro.Guillermo Sapiro 第 9 课。
-
由于对图像处理的了解也来自与该课程,没正经儿看过几本图像方面的书籍,有些术语只能用视频中的英文来表达,见谅哈!
1. Uniqueness
假设我们已知字典矩阵 D 和稀疏向量 a, 计算出一个信号 x,即 Da = x, x 存在一个关于 D 的稀疏表示。反过来现在已知前面的 D 和 x,根据 L0 的优化问题,可以归纳为:
的解是唯一的吗?
显然不一定。比如, D 中某些 atoms 恰好相等,或者 column1 = column2 + column3, 以前由 column2 和 column3 现在只用 column1 表示即可。当然也有正面的例子,比如 DCT 变换, 基向量完全正交,解是唯一的。这与 D 中 atoms 的不相关性和数目 K 有关。
2. Sparse Coding
和上面一样,现有字典 D 和带有噪声的信号 y,进行稀疏编码的问题可以表示的 L0 优化问题:
这是一个组合优化问题。假设 alpha 的非零项数目为 L (sparse Level), 先令 L = 1, 每一个列向量尝试一遍,看看是否又满足条件的,共有 K 种组合。如果没有,再令 L = 2, 再次尝试,共有 K(K-1)/2 中组合。还没有满足条件的,则令 L = 3......组合的数目呈指数增长,这是一个 NP-hard 的问题。 实际应用中的 K = 1000, L = 10, 要穷尽所有的排列组合大概需要计算几百万年,因此要采用近似算法, 目前主要有 relaxation methods 和 greedy methods。
-
Relaxation Methods - the Basis Pursuit (BP)
我们知道, L0 norm 可以数出向量中非零 entries 的数目,具有很好的现实意义,但是由于它数学特性(求导等)极差,非常不适合作为一个优化模型中目标函数。在线性分类器中,你可以把误分点的数目作为目标函数,但是没法优化,所以,我们看到的线性分类器的的目标函数一般是 L1 norm(感知器算法), L2 norm(LMS 算法和最小二乘法)以及最大熵(Logistic Regresson)等,也能达到比较好的效果。在上一篇博客中,可以看到 L1 是菱形, L2 是球体,L1 具有更好的稀疏性(解更靠近坐标轴),所以我们采用松弛方法将 L0 norm 转换为 L1 norm:
虽然我们把 count number 变成了 count the magnitude, 但是在某些条件下,上式的解与松弛之前的解等价。上述方法也叫 BP,新定义的问题是一个凸优化问题,解决的方法很多,有 Interior Point methods, Sequential shrinkage for union of ortho-bases, Iterative shrinkage 等。 -
Greedy Methods - Matching Pursuit (MP)
第一步,找到最接近(平行) y 的 atom, 等效与在 alpha 向量上仅取一个非零项,求出最接近的 atom, 保留下来
第二步,计算误差是否满足要求,如果满足,算法停止,否则,计算出残差信号,和第一步类似,找到最接近残差向量的 atom, 保留下来
第三步,调整已选向量的系数,使得 Da 最接近 y,重复第二步 (OMP, Orthogonal Matching Pursuit)
总结一下解决这个问题的算法有:

3. Dictionary Learning - K-SVD
字典学习的一个假设是——字典对于一张 good-behaved 的图像具有稀疏表示。因此,选择字典的原则就有能够稀疏地表达信号。有两种方法来设计字典,一种是从已知的变换基中选择,或者可以称为 beyond wavelet 变换,比如 DCT 实际上就是一个稀疏表示(高频部分系数趋向于 0),这种方法很通用,但是不能够 adapted to the signal。第二种方法是字典学习,即通过已有的大量图片数据进行训练和学习。
比如,现在有 P 个信号(张图片)要进行稀疏表示,如何学习一个字典?
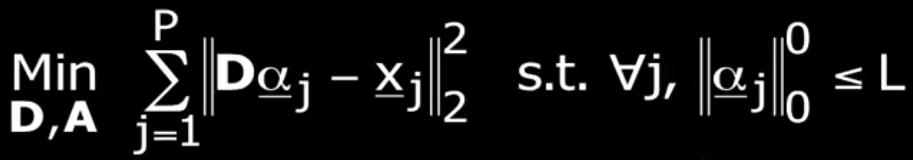
上式字典矩阵 D 和 alpha 组成的稀疏表示 A 矩阵都是可变量,目前有几种算法解决这个问题,下面介绍 K-SVD 算法(K-Means的一种变种),idea 非常简单。假设现在有原始信号矩阵 X^T, 该矩阵的每一行表示一个信号或者一张图片, D 矩阵是字典矩阵,右下方是 sparse coding 矩阵,红色的点表示非零项:
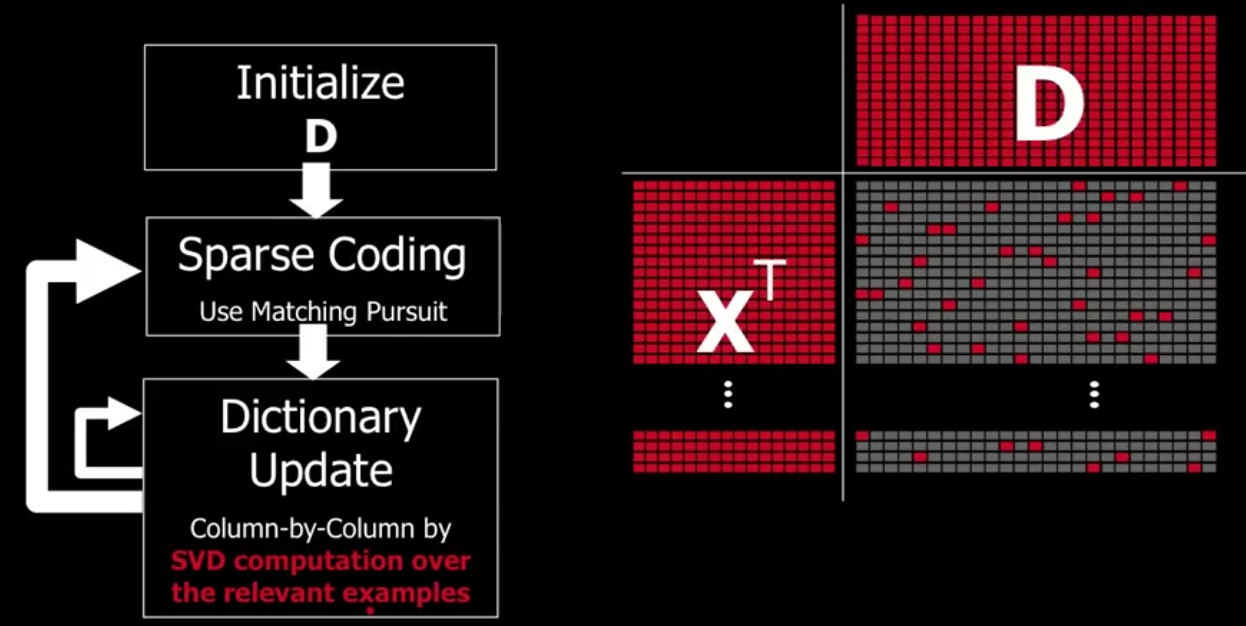
算法步骤如下:
Step 1: Initialize。在 X^T 矩阵中随机挑选一些行向量(一些原图),填满矩阵 D。( K-means 随机选点初始化)
Step 2: Sparse Coding. 用上一小节的方法(松弛或者贪婪法)进行稀疏编码,Row-by-Row 计算出稀疏矩阵。
Step 3: Dictionary Update. 字典以列向量为基,自然要 Column-by-Column 地更新字典。比如现在更新某一列, 下方对应的红点,根据红点找到对应的信号(图像),然后除掉其他不相关的图像,得到示意图如下:
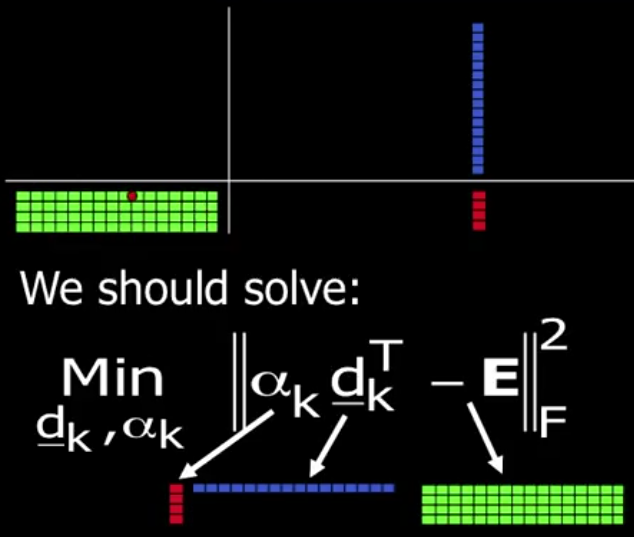
上图中字典的 atom 对四张图片都有贡献,我们调整 atom 的目的是使得这个贡献更大,从而使稀疏性表示效果更好。当然,一个 atom 只能表示一条直线,三张图片的信号极有可能不在这条直线上,我们要做的是将中间的误差降到最小,这其实就是一个最小二乘(MSE)的问题。具体做法是将最右下角的矩阵进行 SVD 分解(SVD 相关知识可参考之前我写的博客),找出主成分,然后回到 Step2, 迭代。