课程地址:https://www.coursera.org/learn/machine-learning/lecture/8SpIM/gradient-descent
此篇博文是我在聆听以上课程的笔记,欢迎交流分享。
一 Model and Cost Function 模型及代价函数
1 Model Representation 模型表示
首先,教授介绍了一下课程中将会用到的符号和意义:
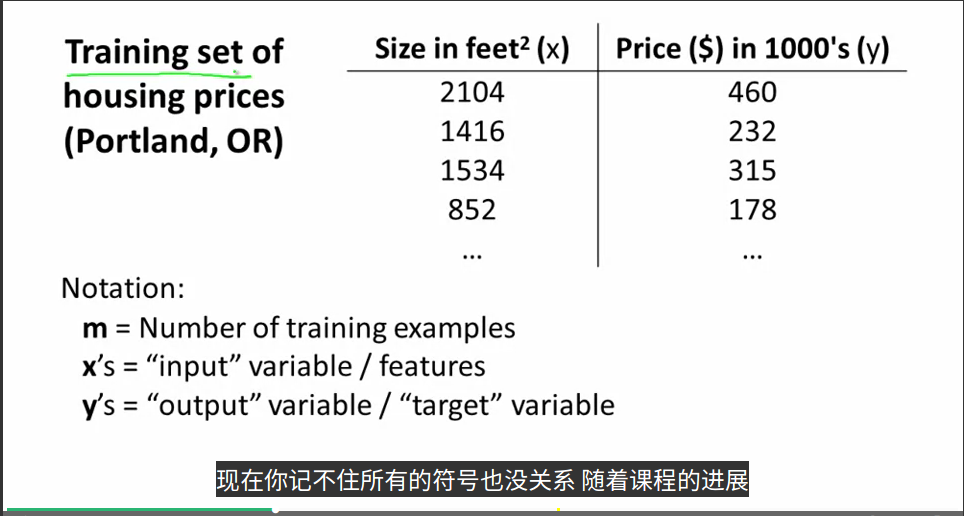
m:训练样本的数目
x:特征量
y:目标变量
(x,y):一个训练样本
(x^(i),y^(i)):i不是指数,而是指第i行的样本
Univariate linear regression:一元线性回归
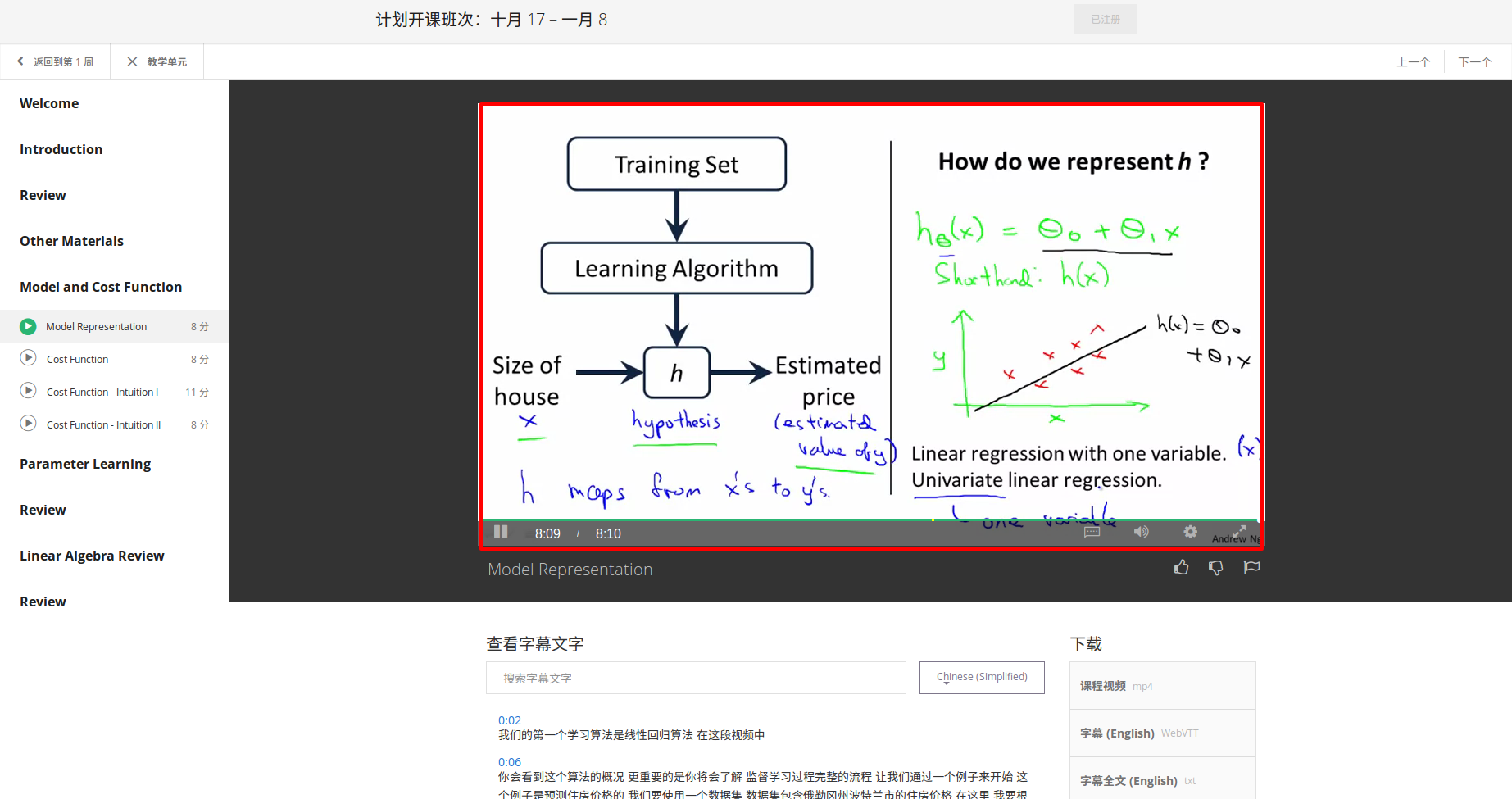
2 Cost Function 代价函数
整体目标函数 --> 代价函数(平方误差函数,平方误差代价函数)

二 Gradient Descent 梯度下降
梯度下降算法可以将代价函数j最小化。梯度函数是一种很常用的算法,它不仅被用在线性回归上,也被广泛地应用于机器学习领域中的众多领域之中。
下图是代价函数J中解决线性回归问题的问题概述:

我们希望通过改变theta参数的值来最小化代价函数。
这里,我们考虑有两个参数的情况,我们可以考虑到一个三维图形,两条坐标分别表示theta0和theta1。
梯度下降要做的事,就是从某个起始theta对值开始,寻找最快的下降方向往下走,在路途上也不断地寻找最快下降的方向更改路线,最后到达一个局部最低点。
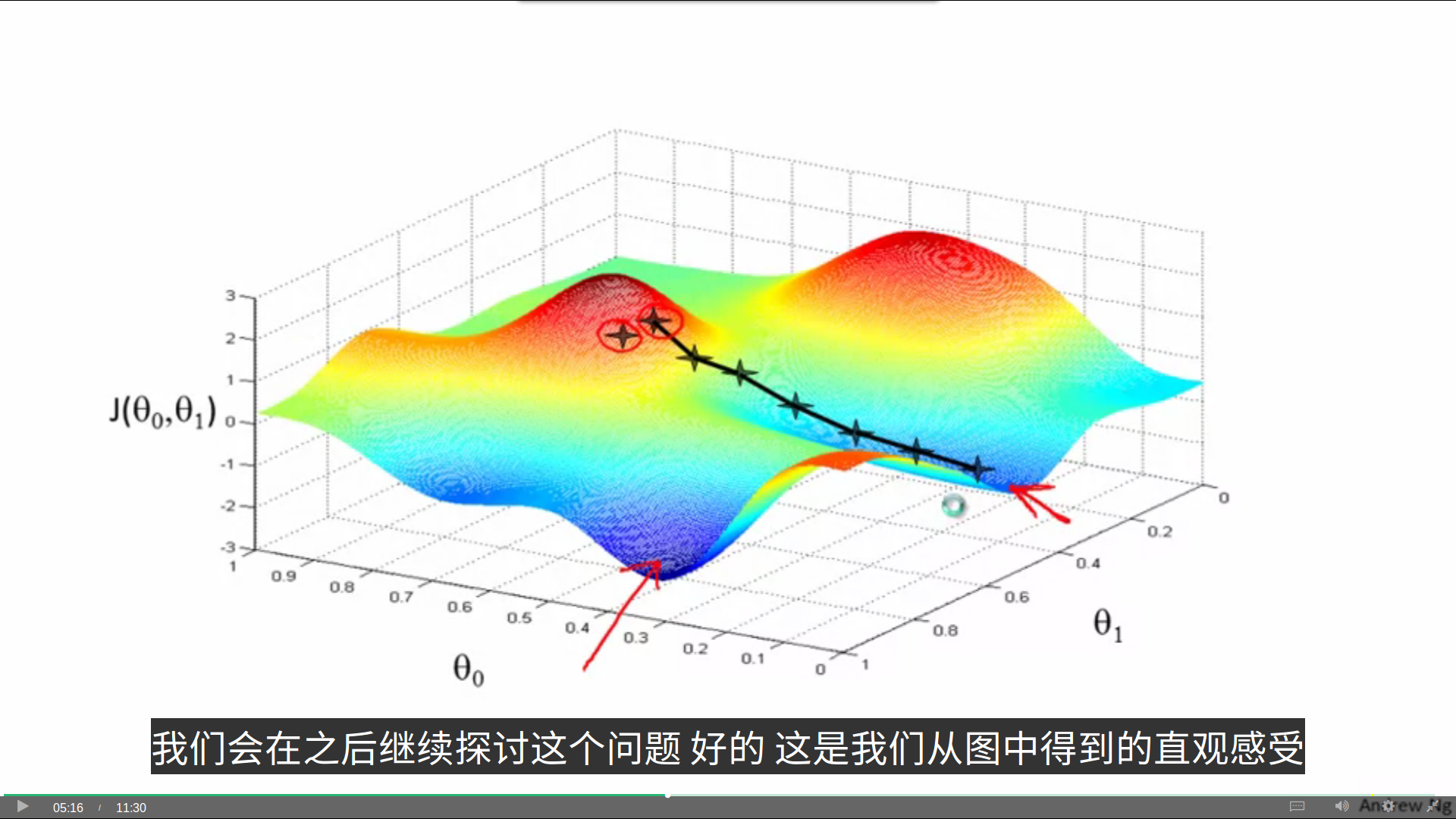
可以看到,如果起始点稍有偏差,那么我们可能会得到一个非常不同的局部最优解,这也是梯度下降的一个特点。
我们从上图中获得了梯度下降的直观感受,接下来让我们看看梯度下降的定义:

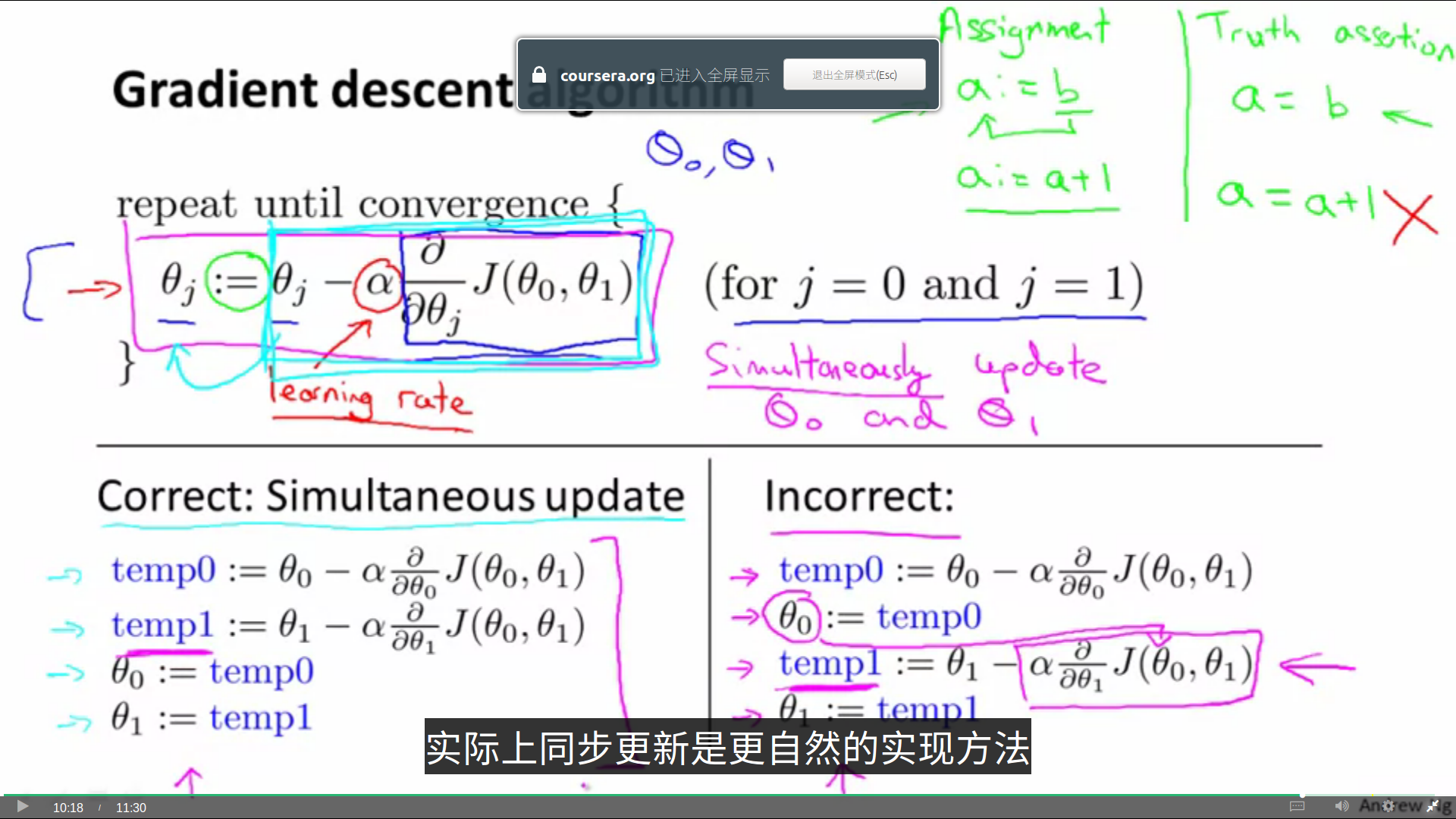
分析一下梯度下降定义公式的一些细节:
我们用“:=”来表示赋值。注意,如果我们写作“=”,表达的意识并不是赋值,而是判断为真的说明,比如a=b,就是断言a的值是等于b的。
α在这里是一个数字,被称为学习效率(learning rate),在梯度下降算法中,它控制了我们下山时会卖出多大的步子。因此如果α比较大,那我们用大步子下山,如果它比较小,我们就迈着很小的小碎步下山。
在公式中,有一个很微妙的问题。在梯度下降中,我们要同时更新theta0和theta1,而不是先后更新。如果先更新了theta0,再更新theta1就会造成theta1的值出错。
三 Gradient Descent Intuition 梯度下降的客观事实
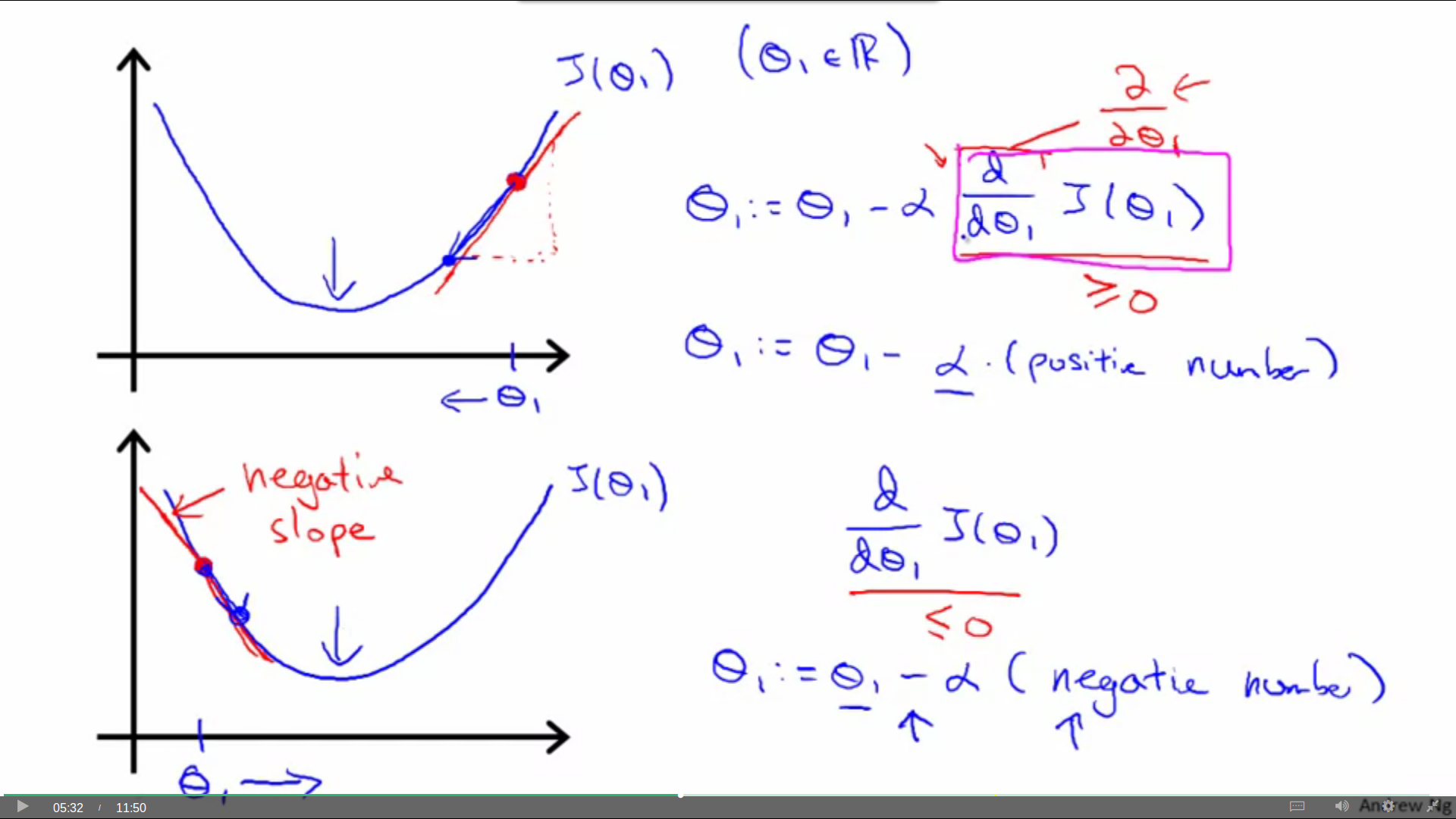
首先,教授向我们介绍了一下倒数和偏导的概念。教授为了解释明白,说了很长一段话,大概的意思就是,导数在梯度下降中的存在就是为了指出方向,指示我们向局部最低点进发。
然后,就是α的问题。我们来讨论一下学习效率α大小对我们下山的影响:

总结一下:α太小,那我们就像小宝宝一样往下爬得超级慢,但如果α太大,就可能一步跨过了最低点,甚至南辕北辙,无法收敛反而发散出去了。
那如果我们恰好就在或者刚好走到了局部最低点呢?感受一下,这个时候导数是0,这是在告诉我们不要再走啦,不管步子迈多大,都只是原地踏步。所以此时就不再更新theta的值了。

α值都固定了,梯度下降为什么也可以让代价函数收敛到一个局部最低点呢?

事实上,我们并不会跨着相同的步子在最低点两端徘徊做无用功。因为导数不仅为我们指明了方向,也在影响我们每一步的大小。
当我们接近一个局部最低点时,梯度下降也会自然第把步子跨小。所以,没有必要减小α。
三 Gradient Descent For Linear Regression 梯度下降在线性回归中的应用
为了了解梯度下降法的应用,我们需要首先对梯度下降公式中的导数项进行分析:
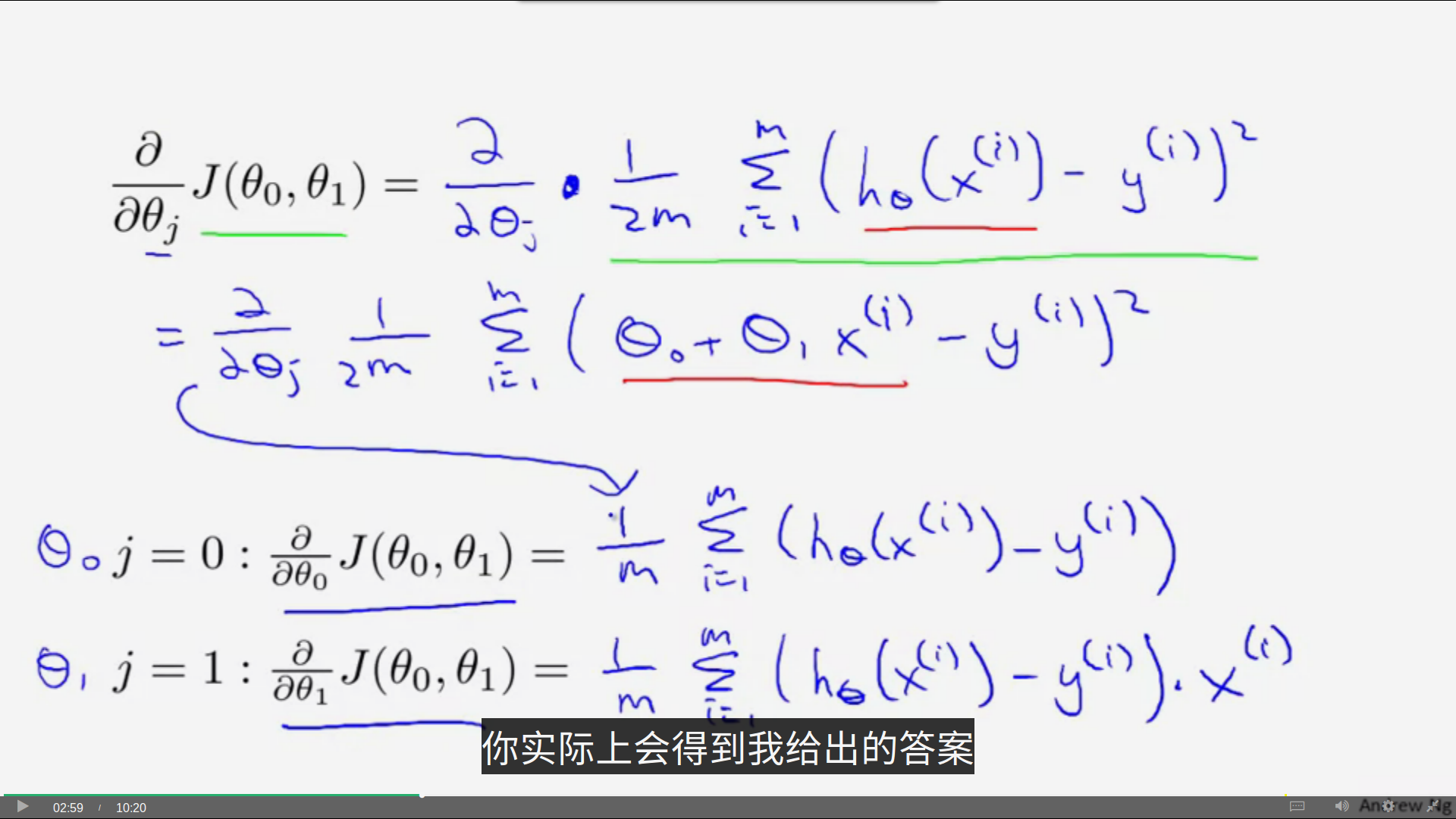
于是,我们直接得到了更新theta0和theta1的公式(如上图)。要推导这个公式需要一定的微积分基础,如果不熟悉也没有关系,你可以直接应用公式:

事实证明,用于线性回归的代价函数总是一个凸函数(convex function),因此,这个函数没有任何局部最优解,只有一个全局最优解。并且无论什么时候,你对这种代价函数使用线性回归/递归下降法得到的结果,都会是收敛到全局最优值的。因为没有全局最优以外的其他局部最优点。

最后,我们刚刚使用的算法有时也被称为“批量梯度下降法”,意思是——在梯度下降的每一步中,我们最终都要计算所有m值代价的求和运算,所以“批量梯度算法”也是指“一批”训练集“。
