（堆的应用）Huffman赫夫曼树的建立

日后的纠正

最近才发现自己的代码有问题，也是在后来做另一个有关哈夫曼实验的时候才发现，在代码当中有很多时候是用new来建立一个新的节点，就包括从最小堆中取出权重最小的节点（这个没有错误），根据两个权重最小节点得出新的节点和往最小堆中插入这个新的节点。问题出在后两个，因为在中间那一步就对left和right设置了parent（看了我的代码的就该很清楚了），其实如果这样下去是很繁琐的，因为new来new去，赋值来赋值去，非常容易搞混。

我测试了一下，会把一部分孩子（left或者right）的parent指针搞错，所以今天2011-12-17我更新了Huffman哈夫曼代码。另外值得一提的是，网络上我看了很多类似的代码，发现有很多是错误的，而最重要的错误就在这里。

建立Huffman树的基本思路：给定有权重的一系列数据（带权重），从中挑选最小权重的两个数据，组成一棵树，得到的父节点再插入到数据系列当中。

开始的时候按着严老师的办法，是借助顺序表来完成Huffman树的建立；同样，在建树过程中要从顺序表中选择比较小的两个数，相加后再插入到表尾，如此往复，直到所有给出的点都插入为止。通过最小堆来建树也很灵活便捷。堆的性能高，排序时间复杂度为nlog(2)n，利用最小堆，就可以将很快找出最小的元素（总是在顶部）。

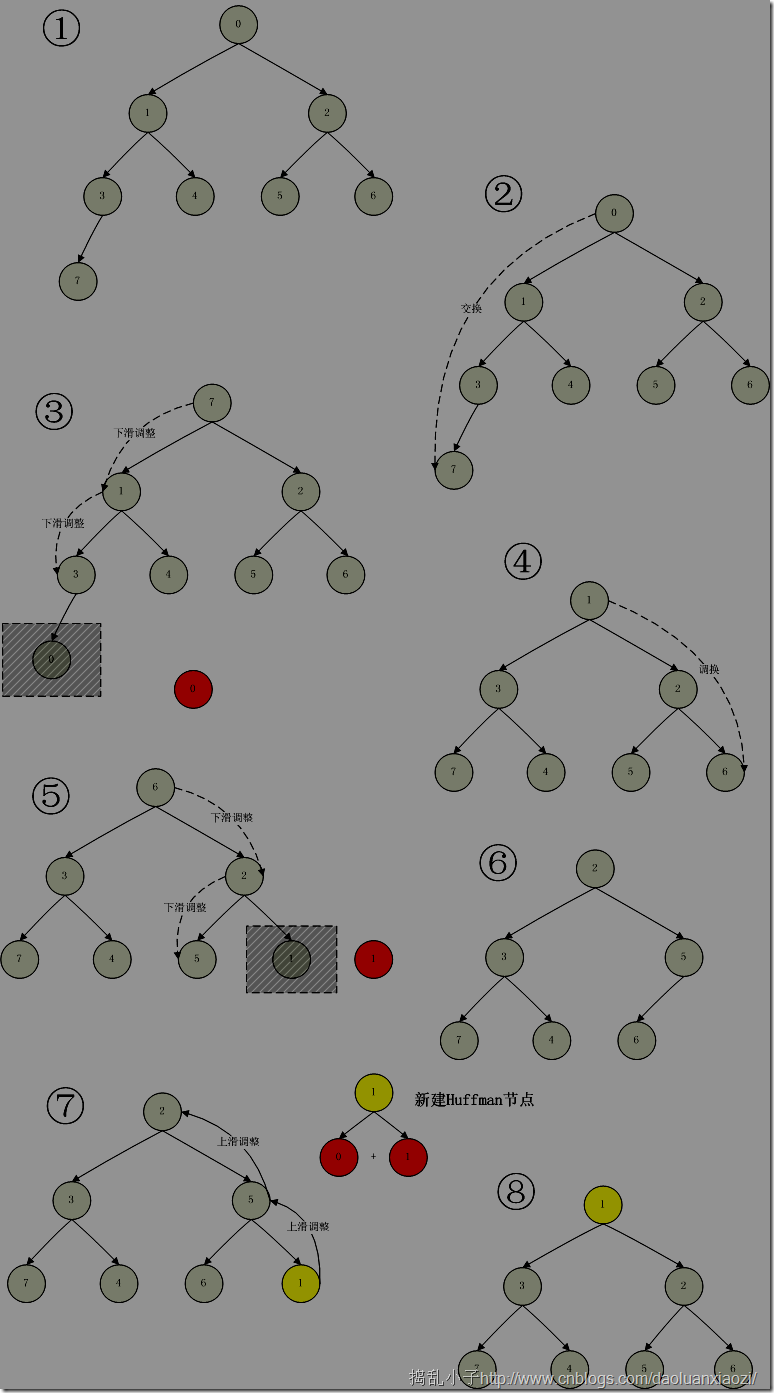
下面8步立刻掌握利用最小堆来建立Huffman树。

看图解说

①原图（已经是最小堆）；

②交换堆的首元素（权重肯定是最小的）和最后一个元素对换；

③交换后删除最后一个元素（复制出来），其实也不是真正的删除，只是size-1这个操作而已；调换后就不是堆了，重新调整heap为最小堆，调整可以用递归调用，也可以用下标作为判断条件，我的代码用的是下标判断条件；

④继续②；

⑤弹出权重最小的，调整；将权重两个最小点复制出来后，组成新的父节点，调整他们之间的内部指针关系；

⑥调整后；

⑦插入新节点，调整；

⑧调整后。

以上做了第一遍的操作，继续做下去知道堆中只剩下最后一个元素为止，再将root指向其就可以了，下面是代码。如此下来，Huffman树就建好了。

ps:下面的代码在建立最小堆和在堆中取出权重最小Huffman节点的时候，因为在HuffmanNode设计过程当中没有加入weight（权重），因此就姑且用了data（int型）的值作为权重。

Huffman节点数据结构设计：

#ifndef _HUFFMANNODE_H_
#define _HUFFMANNODE_H_

struct HuffmanNode				//Huffman节点定义
{
private:
	int data;

public:
	//构造函数
	HuffmanNode * left,* right,* parent;
	HuffmanNode():left(NULL),right(NULL),parent(NULL),data(-1){}
	HuffmanNode(int d):left(NULL),right(NULL),parent(NULL),data(d){}

	//重载运算符
	HuffmanNode &operator=(const HuffmanNode& hn)
	{
		left = hn.left;
		right = hn.right;
		data = hn.data;
		return *this;
	}

	//数据的获取和维护
	int GetData()const{return data;}						//获取数据
	bool SetData(int d){data = d;return true;}		//设置数据
};

#endif

最小堆类：

#include <iostream>
using namespace std;

#ifndef _MINHEAP_H_
#define _MINHEAP_H_

#include "HuffmanNode.h"

const int DefaultSize = 100;

class MinHeap
{
	HuffmanNode * heap;
	int szCurrent;

public:
	MinHeap(int sz = DefaultSize);
	~MinHeap()
	{delete [] heap;}

	void CreateMinHeap(int arr[],int n);		//数组构建最小堆
	bool Insert(HuffmanNode * e);				//往堆中插入Huffman节点
	void SiftDown(int start,int m);				//下滑，重建最小堆
	void SiftUp(int start,int m);					//上滑，在插入的时候用到
	HuffmanNode * GetMinNode();				//获取Huffman节点data值最小的节点，同时维护szCurrent
	bool SwapNode(int i,int j);						//交换下标为i和j的Huffman节点
	void Print();											//打印Huffman节点
};

#endif

#include <iostream>
using namespace std;
#include "MinHeap.h"
#include <assert.h>

MinHeap::MinHeap(int sz)
{
	heap = new HuffmanNode[sz];
	assert(heap!=NULL);
	szCurrent = 0;
}

void MinHeap::CreateMinHeap(int arr[],int n)
{
	this->heap = new HuffmanNode[DefaultSize];
	assert(heap!=NULL);

	int i;
	for(i=0; i<n; i++)
		heap[i].SetData(arr[i]);

	szCurrent = n;

	int currentpos = (szCurrent-2)/2;			//从最后一个顶点开始调整
	while(currentpos >= 0)
	{
		SiftDown(currentpos,szCurrent-1);
		currentpos -- ;
	}
}

void MinHeap::SiftDown(int start,int m)
{
	int i = start,j = i*2+1;
	HuffmanNode temp = heap[i];
	while(j<=m)	
	{
		if(j<m && heap[j].GetData() > heap[j+1].GetData())			//j记录比较小的子节点
			j++;

		if(temp.GetData() <= heap[j].GetData())			//不调整
			break;
		else
		{
			heap[i] = heap[j];			//子节点上移
			i = j;
			j = 2*j+1;
		}
	}
	heap[i] = temp;
}

void MinHeap::SiftUp(int start,int m)
{
	int j = start,				//子节点位置
		i = (start-1) / 2;	//顶点位置
	HuffmanNode temp = heap[j];	//记录子节点
	while(j > 0)
	{
		if(temp.GetData() > heap[i].GetData())			//不调整
			break;
		else
		{
			heap[j] = heap[i];			//顶点下滑
			j = i;
			i = (i-1) / 2;
		}
	}
	heap[j] = temp;
}

void MinHeap::Print()
{
	for(int i=0; i<szCurrent; i++)
		cout << heap[i].GetData() << " ";
	cout << endl;
}

bool MinHeap::Insert(HuffmanNode * e)
{
	szCurrent++;
	if(szCurrent > DefaultSize)
		abort();
	
	heap[szCurrent-1] = *e;
	SiftUp(szCurrent-1,0);			//调整
	return true;
}

HuffmanNode * MinHeap::GetMinNode()
{
	if(szCurrent>0)
	{
		HuffmanNode * t;
		SwapNode(0,szCurrent-1);		//此时heap[0].data是最小的，让它跟最后一个元素调换
		szCurrent--;
		SiftDown(0,szCurrent-1);
		t = new HuffmanNode();
		* t = heap[szCurrent];
		cout << "GetMinNode()后得到的堆：";
		Print();
		return t;
	}
	return NULL;
}

bool MinHeap::SwapNode(int i,int j)
{
	swap(heap[i],heap[j]);
	return true;
}

Huffman类：

#include "MinHeap.h"

#ifndef _HUFFMANTREE_H_
#define _HUFFMANTREE_H_

class Huffman
{
	MinHeap * mh;					//堆，协助建立Huffman树
	HuffmanNode * root;			//Huffman树的根节点

public:
	Huffman():root(NULL){};
	~Huffman()
	{
		delete mh;
		MakeEmpty(root);
	}
	void MakeEmpty(HuffmanNode * ptr)
	{
		if(ptr->left)
			MakeEmpty(ptr->left);
		if(ptr->right)
			MakeEmpty(ptr->right);
		delete ptr;
	}
	void CreateHuffmanTree(int arr[],int size);
	void Print();
	void Adjust(HuffmanNode * ptr);
};

#endif

#include <iostream>
using namespace std;
#include <assert.h>
#include "HuffmanTree.h"
#include "MinHeap.h"
#include <queue>

void Huffman::CreateHuffmanTree(int arr[],int size)
{
	mh = new MinHeap(size);
	mh->CreateMinHeap(arr,size);			//将数据建立最小堆
	int i;
	HuffmanNode * left;
	HuffmanNode * right;
	HuffmanNode * parent;

	for(i=0; i<size-1; i++)
	{
		left = mh->GetMinNode();			//较小成为左孩子
		right = mh->GetMinNode();			//较大成为右孩子

		//这里可以归结出一个函数来，但是有点麻烦，直观点
		parent = new HuffmanNode(left->GetData()+right->GetData());
		parent->left = left;
		parent->right = right;
		left->parent = right->parent = parent;

		if(!mh->Insert(parent))
			abort();

		cout<< "插入父节点之后的堆：";
		mh->Print();
	}
	root = parent;
}

void Huffman::Print()
{
	queue<HuffmanNode *> q;
	q.push(root);
	HuffmanNode * p;
	while(!q.empty())
	{
		p = q.front();
		cout << p->GetData() << " ";
		if(p->left != NULL)
			q.push(p->left);
		if(p->right != NULL)
			q.push(p->right);
		q.pop();
	}
}

void Huffman::Adjust(HuffmanNode * ptr) //添加“调整”函数以调整孩子的父节点指针
{
	HuffmanNode * p, * q;
	if(ptr->left || ptr->right)
	{
		p = ptr;
		if(p->left)
		{
			q = ptr->left;
			q->parent = p;
		}
		if(p->right)
		{
			q = ptr->right;
			q->parent = p;
		}
		Adjust(p->left); 
		Adjust(p->right);
	}
}

Huffman（哈弗曼，赫夫曼）在通信领域用途很大，在文件压缩技术也有所运用，做些笔记，以后有用，与大家共享，欢迎讨论:)。

捣乱小子 2011-12-15