哈夫曼压缩算法

编程独白

给你40分钟的时间，你可以思考十分钟，然后用三十分钟的时间来写代码，最后浪费在无谓的调试上；你也可以思考半个小时，彻底弄清问题的本质与程序的脉络，然后用十分钟的时间来编写代码，体会代码如行云流水而出的感觉。在编程过程当中，相信大家都深有体会，在调试上浪费时间，问题出现在下笔之前没有一个系统结构。

关于哈夫曼

哈夫曼在通信领域有很多的用途，将需要传输的数据转换01串，相比直接传输，极大提高了传输的速率，同时还在数据压缩的重要方法。而本篇主要介绍的是哈夫曼压缩算法。

哈夫曼树创建

哈夫曼树创建用了两种的方法，一种是基于顺序表，另一种是基于最小堆。关于这两种方法可以参考：

• 基于顺序表哈夫曼树

• （堆的应用）Huffman赫夫曼树的建立（推荐）

建立Huffman树的基本思路：

给定有权重的一系列数据（带权重），从中挑选最小权重的两个数据，组成一棵树，得到的父节点再插入到数据系列当中。

哈夫曼压缩思路

假设一字符串是，“abcabcabcabcabcabcddddddddd”，统计各字符出现的次数如下表。

字符	出现次数
a	6
b	6
c	6
d	9

按照一搬的存储方法，一个字符占用一个字节，那么共花费(6+6+6+9)*sizeof(char) = 27字节，27字节确实不算什么，但是如果是海量数据的时候，就可能要考虑存储空间的问题了。

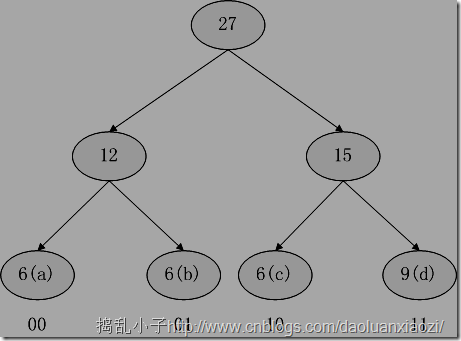
来看看哈夫曼压缩算法是怎么做的，同样是上面的例子，我们试着建立哈夫曼树，出现的次数就当做是权重，出现的次数越多的话，越靠近根节点，那么编码越短，如下图：

于是上面的“abcabcabcabcabcabcddddddddd”，就可以转化为“0001,1000,0110,0001,1000,0110,0001,1000,0110,1111,1111,1111,1111,11”，注意这里采用的按位存储的，也就是说0和1都是位，而非char型。那么之前的27字节就被我们转换成了7个字节（7字节不足，不足的话就补零），而这就达到了压缩的效果。

所以总结一下：利用哈夫曼树编码的特点，权重越大越靠近根节点，得到的编码就越短的原理，而如果把字符出现次数作为权重的话，文本当中出现次数最多的字符就被压缩成了很短的编码。

哈夫曼压缩详解

·压缩过程主要步骤如下：

1. 统计：读入源文件，统计字符出现的次数（即统计权重），顺便根据权重进行从大到小的排序（主要的话之后的操作会简单一些）；
2. 建树：以字符的权重（权重为0的字符除外）为依据建立哈夫曼树；
3. 编码：依据2中的哈夫曼树，得到每一个字符的编码；
4. 写入：新建压缩文件，写入压缩数据。

其中最为复杂的是步骤4，因为它涉及到了位的操作，待我细细道来。

假设一字符串是，“acbcbacddaddaddccd”，统计各字符出现的次数如下表。

字符	出现次数
a	4
b	2
c	5
d	7

哈夫曼树 

 

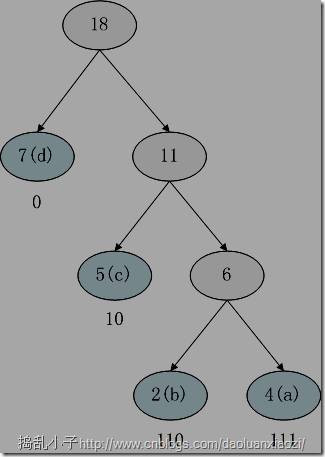
步骤123统计，建树，编码都已经完成了，剩下写入压缩文件。将字符串一步一步翻译成01串，

• a:111
• ac:1111 0
• acb:1111 0110
• acbc:1111 0110 10
• acbcb:1111 0110 1011 0…

似乎都很顺利，但是位操作有点麻烦。首先申请足够大的内存，比如已知文本字符个数是1000个字符（字节），可以申请1000*4，即一个字节平均4字节（32位）的压缩编码空间（已经足够大了），别把这些看成是char型了，当作位来看。

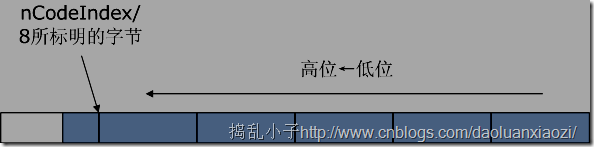
声明nCodeIndex作为已编码的位数，相当于counter。刚申请的足够大的内存以8位划分，那么可以发现：

• nCodeIndex/8可以标明第一个未存满的字节，相当于nCodeIndex>>3；

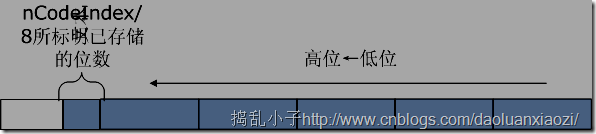
• nCodeIndex%8可以标明第一个未存满的字节当中有几位已经完成了存储，相当于nCodeIndex&7。

可能说的不够清楚，所以画了图:

*(long *)(pDest+(nCodeIndex>>3)) |= (p->code) << (nCodeIndex&7);（其中p为哈夫曼节点）

如此一来，我们就可以很理直气壮的将*(long *)(pDest+(nCodeIndex>>3))赋值为*(long *)(pDest+(nCodeIndex>>3)) | (p->code) << (nCodeIndex&7)（0|X=X），而不用担心到底*(long *)(pDest+(nCodeIndex>>3))里面到底有多少位已经是存储了的。

给出压缩主要代码：

void CompressHuffman(char * filename)
{
	//·统计权重
	int count = Statistics(filename);

	Huffman hf;
	hf.CreateHuffmanTree(acsii,count);

	//·测试
	//hf.Print();

	//根据生成的哈夫曼树，为每个字符生成编码
	EnCode(&hf,count);
	HuffmanNode * root = hf.GetRoot();

	fstream fshuff;
	fshuff.open("data.huff",ios::binary|ios::out);

	//写入压缩文件的工作流程如下：

	//·数据个数（字符出现的个数）
	//·每个数据（data）以及其权重（rate）
	//·源文件中的字符个数，如源文件为abcd123，那么字符个数为7
	//·编码的长度
	//·编码

	//·写入字符个数，比如abdarr，字符个数是4
	fshuff.write((char *)&count,sizeof(int));

	//·写入acsii值和权重，以便在解压缩的时候重建哈夫曼树
	unsigned int  i;
	for(i=0; i<count; i++)
	{
		//·这里的读写可能会有问题的
		fshuff.write((char *)&(acsii[i].data),sizeof(char));
		fshuff.write((char *)&(acsii[i].rate),sizeof(int));	
	}

	//·注意区别fs和fshuff，前者是源文件，后者是压缩后的文件
	fstream fs(filename,ios::in|ios::binary);

	//·获取源文件文件字节数大小，seekg用在读中，seekp用在写中
	fs.seekg(0, ios_base::end);
	long nFileLen = fs.tellg();
	fs.seekg(0,ios::beg);

	//·将源文件逐个写入到压缩文件当中
	char * pDest = new char [nFileLen];
	for(i=0; i<nFileLen; i++)		//·清零，不清零会出现致命性的错误
		*(pDest+i) = 0;

	unsigned int nCodeIndex = 0;

	char * temp = new char[nFileLen+1];
	fs.read(temp,nFileLen);

	HuffmanNode *  p;
	for(i=0; i<nFileLen; i++)
	{
		//·在acsii表当中
		p = GetCodeFromACSIITable(temp[i],count);
		assert(p != NULL);

		*(long *)(pDest+(nCodeIndex>>3)) |= 
			(p->lCode) << (nCodeIndex&7);

		nCodeIndex += p->nCodeLen;
	}
	//·写入源文件的字符个数
	fshuff.write((char *)&nFileLen,sizeof(long));


	//·写入编码长度
	fshuff.write((char *)&nCodeIndex,sizeof(int));

	unsigned int  nDestLen = nCodeIndex/8;
	if(nDestLen*8 < nCodeIndex)
		nDestLen ++;

	//·写入编码
	fshuff.write(pDest,nDestLen);
	fshuff.close();
	fs.close();
}

简介哈夫曼压缩文件DL结构

前一段时间在接触位图的时候被位图结构触动了，感觉它存储得有条理，于是萌生了为哈夫曼压缩文件定义一个存储结构，称之为哈夫曼压缩文件DL结构。关键是要统一，这篇博文用的是一种结构，另一篇用的又是另一种，纷杂的样式会让初学者发晕，所以统一结构对于学习哈夫曼压缩文件会有很大的帮助。

DL结构组成部分：

• 节点个数-用以规定创建哈夫曼树节点个数，以便读入节点域；
• 节点域-用以创建哈夫曼树和产生字符编码；
• 源文件字符数-在解压的时候有用；
• 编码长度（以位为单位）-源文件编码的总长度，以位为单位；
• 编码域-存储所有字符编码的存储域。

为了便于让你不看文字就能明白，看下图，按着这种结构就相当于有了大概的思路。

 

哈夫曼解压详解

解压的过程就简单很多了，因为一些代码已经在解压过程当中完成，比如哈夫曼树的建立，我们只要设计压缩和解压通用的接口，就可以很简单的按照编码域的内容，将编码翻译成原文。

1. 读入节点个数；
2. 根据1，读入节点域；
3. 创建哈夫曼树；
4. 读入编码长度；
5. 根据4，读入编码域；
6. 翻译；
7. 写入解压后的文件。

根据编码长度（以bit为单位），可以计算出编码域的大小（以byte为单位），读入编码域就很方便了。其中翻译部分我给出一部分代码，根据哈夫曼树，将编码域的01串按位处理，转换为字符。

• Code&1判断最低位是0还是1，从而决定指向left还是right；
• Code>>=1，将Code右移，方便处理下一位；
• 每当翻译出一个字符，就要将当前的哈夫曼指针重新指向root，p = hf.GetRoot()。

	for(i=0; i<nFileLen-1;)		//·特地少处理一个字节
	{
		Code = *(temp+(nSrcIndex));
		for(int j=7; j>=0; j--)
		{
			p = (Code&1) ? p->right : p->left;
			if(!p->left && !p->right)
			{
				*(pDest+i) = p->data;
				p = hf.GetRoot();
				i++;
			}
			Code>>=1;			//·为了处理下一位，右移一位
		}
		nSrcIndex ++;
	}

	Code = *(temp+(nSrcIndex));
	for(int j=0; j<nOffset; j++)
	{
		p = (Code&1) ? p->right : p->left;
		if(!p->left && !p->right)
		{
			*(pDest+i) = p->data;
			cout << p->data << endl;
			p = hf.GetRoot();
		}
		Code>>=1;			//·为了处理下一位，右移一位
	}

附哈夫曼压缩算法工程：哈夫曼压缩算法.rar

本文完。Monday, December 26, 2011