Red Black Tree（红黑树）

　　（修改于 2018-05-06 15:53:22 　　还差删除维护操作、层序遍历没完成。维护操作没完成不想写层序遍历怎么办。。。）

　　今天下午完成了红黑树的插入的维护操作，但删除的维护操作还没有解决，删除的维护很麻烦...所有的删除会导致的情况我都理清楚了，但暂时没有想到好的算法来组合这些情况（orz...）。

　　实际上之前思维被《算法导论》中给的出算法思路固定了，导致一直想要在算导的红黑树算法基础上完成，后来觉得算导中给的伪码有些地方有问题，于是开始思考自己独立实现红黑树算法。当然没有算导给出的思路以及理解，我肯定也不能独立写出来。现在看来红黑树的维护情况确实比较复杂，个人觉得比AVL树的要复杂许多，但也或许是我想的算法过于复杂。总之，代码后面在说吧。

　　code:

/*
 * RBT.c
 *
 *  Created on: 2017年11月18日
 *      Author: darkchii
 */

#include <stdio.h>
#include <stdlib.h>
#include <conio.h>

#define max(a, b) ((a) > (b) ? (a) : (b))

#define bool int
#define true 1
#define false 0;

typedef int ElemType;
typedef enum {RED, BLACK} ColorTree;
const char ColorBoolean[] = "RB";

typedef struct BaseNode {
    ElemType val;
    ColorTree Color;

    struct BaseNode*Left;
    struct BaseNode*Right;
    struct BaseNode*Parent;
}rb_tree;

rb_tree*Initialize();
bool IsBlack();
bool IsRed();
int CurrentBlackHeight();
int Depth();
int Degree();
rb_tree*parent();
rb_tree*uncle();
rb_tree*grandparent();
rb_tree*sibling();
rb_tree*SearchMinimum();
rb_tree*SearchMaximum();
rb_tree*SearchNode();
rb_tree*LeftRotate();
rb_tree*RightRotate();
void Insert_case_1();
void Insert_case_2();
void Insert_case_3();
void Insert_case_4_1();
void Insert_case_4_2();
rb_tree*InsertNode();
rb_tree*InsertFixup();
rb_tree*Insert();
rb_tree*Transpant();
rb_tree*DeleteNode();
void DeleteFixup(rb_tree*root, rb_tree*delNode);
rb_tree*Delete();
void InOrderTraversal();
void EraseTree();

rb_tree*Initialize(void) {
    rb_tree*root = NULL;

    return root;
}

bool IsBlack(rb_tree*node) {
    return node != NULL && node->Color == BLACK;
}

bool IsRed(rb_tree*node) {
    return node != NULL && node->Color == RED;
}

int CurrentBlackHeight(rb_tree*node) {
    if (node == NULL)
        return 0;
    const int redness = IsRed(node);
    if (redness && (IsRed(node->Left) || IsRed(node->Right)))
        return -1;
    int blackHeight;
    if ((blackHeight = CurrentBlackHeight(node->Left)) < 0)
        return -1;
    if (blackHeight != CurrentBlackHeight(node->Right))
        return -1;

    return blackHeight + !redness;
}

int Depth(rb_tree*node) {
    if(node == NULL)
        return 0;
    return max(Depth(node->Left), Depth(node->Right)) + 1;
}

int Degree(rb_tree*node) {
    if(node == NULL)
        return 0;
    return Degree(node->Left) + Degree(node->Right) + 1;
}

rb_tree*parent(rb_tree*node) {
    if(node == NULL)
        return NULL;
    return node->Parent;
}

rb_tree*grandparent(rb_tree*node) {
    rb_tree*p = parent(node);

    if(p == NULL)
        return NULL;
    return parent(p);
}

rb_tree*sibling(rb_tree*node) {
    rb_tree*p = parent(node);

    if(p == NULL)
        return NULL;
    else if(node == p->Left)
        return p->Right;
    else
        return p->Left;
}

rb_tree*uncle(rb_tree*node) {
    rb_tree*p = parent(node);
    rb_tree*g = grandparent(node);

    if(g == NULL)
        return NULL;
    if(sibling(p) == NULL)
        return NULL;
    return sibling(p);
}

rb_tree*SearchMinimum(rb_tree*minNode) {
    if(minNode == NULL)
        return NULL;
    else if(minNode->Left == NULL)
        return minNode;
    else
        return SearchMinimum(minNode->Left);
}

rb_tree*SearchMaximum(rb_tree*maxNode) {
    if(maxNode == NULL)
        return NULL;
    else if(maxNode->Right == NULL)
        return maxNode;
    else
        return SearchMaximum(maxNode->Right);
}

rb_tree*SearchNode(rb_tree*root, ElemType Data) {
    if(root == NULL)
        return NULL;
    else if(root->val > Data)
        return SearchNode(root->Left, Data);
    else if(root->val < Data)
        return SearchNode(root->Right, Data);
    else
        return root;
}

rb_tree*LeftRotate(rb_tree*root, rb_tree*node) {
    rb_tree*x = node;
    rb_tree*y = x->Right;

    x->Right = y->Left;
    if(y->Left != NULL)
        y->Left->Parent = x;
    y->Parent = x->Parent;
    if(x->Parent == NULL)
        root = y;
    else if(x == x->Parent->Left)
        x->Parent->Left = y;
    else
        x->Parent->Right = y;

    y->Left = x;
    x->Parent = y;

    return root;
}

rb_tree*RightRotate(rb_tree*root, rb_tree*node) {
    rb_tree*x = node;
    rb_tree*y = x->Left;

    x->Left = y->Right;
    if(y->Right != NULL)
        y->Right->Parent = x;
    y->Parent = x->Parent;
    if(x->Parent == NULL)
        root = y;
    else if(x == x->Parent->Left)
        x->Parent->Left = y;
    else
        x->Parent->Right = y;

    y->Right = x;
    x->Parent = y;

    return root;
}

rb_tree*LeftRightRotate(rb_tree*root, rb_tree*node)
{
    rb_tree*x = node;
    rb_tree*y = x->Left;
    root = LeftRotate(root, y);
    root = RightRotate(root, x);
    return root;
}

rb_tree*RightLeftRotate(rb_tree*root, rb_tree*node)
{
    rb_tree*x = node;
    rb_tree*y = x->Right;
    root = RightRotate(root, y);
    root = LeftRotate(root, x);
    return root;
}

/**
void Insert_case_1(rb_tree*root, rb_tree*node) {
    if(parent(node) == NULL)
        node->Color = BLACK;
}

void Insert_case_2(rb_tree*root, rb_tree*node) {
    return ;
}

void Insert_case_3(rb_tree*root, rb_tree*node) {
    parent(node)->Color = BLACK;
    uncle(node)->Color = BLACK;
    grandparent(node)->Color = RED;
    InsertFixup(root, grandparent(node));
}

void Insert_case_4_1(rb_tree*root, rb_tree*node) {
    rb_tree*p = parent(node);
    rb_tree*g = grandparent(node);

    if(node == g->Left->Right) {
        LeftRotate(root, p);
        node = node->Left;
    } else if(node == g->Right->Left) {
        RightRotate(root, p);
        node = node->Right;
    }

    Insert_case_4_2(root, node);
}

void Insert_case_4_2(rb_tree*root, rb_tree*node) {
    rb_tree*p = parent(node);
    rb_tree*g = grandparent(node);

    if(node == p->Left)
        RightRotate(root, g);
    else
        LeftRotate(root, g);
    p->Color = BLACK;
    g->Color = RED;
}
*/

rb_tree*InsertFixup(rb_tree*root, rb_tree*node) {
    /**
    if(parent(node) == NULL)
        Insert_case_1(root, node);
    else if(parent(node)->Color == BLACK)
        Insert_case_2(root, node);
    else if(uncle(node)->Color == RED)
        Insert_case_3(root, node);
    else
        Insert_case_4_1(root, node);
    */

    while(parent(node) != NULL && parent(node)->Color == RED) {
        rb_tree*gptr = grandparent(node);
        if(parent(node) == gptr->Left) {
            if(uncle(node) != NULL && uncle(node)->Color == RED) {
                parent(node)->Color = BLACK;
                uncle(node)->Color = BLACK;
                gptr->Color = RED;
                node = gptr;
            } else if(node == parent(node)->Right) {
                node->Color = BLACK;
                gptr->Color = RED;
                root = LeftRightRotate(root, gptr);
                node = parent(node);
            }
            else {
                parent(node)->Color = BLACK;
                gptr->Color = RED;
                root = RightRotate(root, gptr);
            }
        } else {
            if(uncle(node) != NULL && uncle(node)->Color == RED) {
                parent(node)->Color = BLACK;
                uncle(node)->Color = BLACK;
                gptr->Color = RED;
                node = gptr;
            } else if(node == parent(node)->Left) {
                node->Color = BLACK;
                gptr->Color = RED;
                root = RightLeftRotate(root, gptr);
                node = parent(node);
            }
            else {
                parent(node)->Color = BLACK;
                gptr->Color = RED;
                root = LeftRotate(root, gptr);
            }
        }
    }
    root->Color = BLACK;
    return root;
}

rb_tree*InsertNode(rb_tree*root, rb_tree*newNode) {
    rb_tree*p = root;
    rb_tree*q = NULL;

    while(p != NULL) {
        q = p;
        if(p->val > newNode->val)
            p = p->Left;
        else
            p = p->Right;
    }
    newNode->Parent = q;

    if(q == NULL)
        root = newNode;
    else if(q->val > newNode->val)
        q->Left = newNode;
    else
        q->Right = newNode;
    newNode->Left  = NULL;
    newNode->Right = NULL;
    newNode->Color = RED;

    root = InsertFixup(root, newNode);

    return root;
}

rb_tree*Insert(rb_tree*root, ElemType Data) {
    rb_tree*newNode = (rb_tree*)malloc(sizeof(rb_tree));
    newNode->val = Data;
    return InsertNode(root, newNode);
}

rb_tree*Transpant(rb_tree*root, rb_tree*delNode, rb_tree*graftNode) {
    if(delNode->Parent == NULL)
        root = graftNode;
    else if(delNode == delNode->Parent->Left)
        delNode->Parent->Left = graftNode;
    else
        delNode->Parent->Right = graftNode;

    if(graftNode != NULL)
        graftNode->Parent = delNode->Parent;

    return root;
}

rb_tree*DeleteNode(rb_tree*root, rb_tree*delNode) {
    rb_tree*minNode;
    rb_tree*x;

    if (delNode->Left == NULL && delNode->Right == NULL) {
        x = parent(delNode);
        root = Transpant(root, delNode, delNode->Right);
    } else if(delNode->Left == NULL) {
        x = delNode->Right;
        root = Transpant(root, delNode, delNode->Right);
    } else if(delNode->Right == NULL) {
        x = delNode->Left;
        root = Transpant(root, delNode, delNode->Left);
    } else {
        minNode = SearchMinimum(delNode->Right);
        if (parent(minNode) == delNode) {
             if (minNode->Right != NULL)
                x = minNode->Right;
             else
                x = minNode;
        } else {
            if (minNode->Right != NULL)
                x = minNode->Right;
            else
                x = parent(minNode);
            root = Transpant(root, minNode, minNode->Right);
            minNode->Right = delNode->Right;
            if(minNode->Right != NULL)
                minNode->Right->Parent = minNode;
        }
        root = Transpant(root, delNode, minNode);
        minNode->Left = delNode->Left;
        if(minNode->Left != NULL)
            minNode->Left->Parent = minNode;
        minNode->Color = delNode->Color;
    }
    free(delNode);
    delNode = NULL;
    DeleteFixup(root, x);

    return root;
}

void DeleteFixup(rb_tree*root, rb_tree*node) {
    while(node != NULL) {
        if (node->Left == NULL) {
            
        } else if (node->Right == NULL) {
            if (node->Left != NULL) {
                node->Left->Color = RED;
                node->Color = BLACK;
                if (parent(node) != NULL)
                    parent(node)->Color = RED;
                if (node->Left->Left != NULL)
                    root = RightRotate(root, node);
                else
                    root = LeftRightRotate(root, node);
                if (sibling(node) != NULL)
                    sibling(node)->Color = node->Color;
            }
        } else if(node->Right != NULL) {
            if (node->Color == RED) {
                node->Color = BLACK;
                node->Right->Color = RED;
                if (parent(node) != NULL)
                    parent(node)->Color = RED;
            }
        } else {
            
        }
        node = grandparent(node);
    }
    root->Color = BLACK;
}

rb_tree*Delete(rb_tree*root, ElemType Data) {
    rb_tree*delNode;

    if((delNode = SearchNode(root, Data)) == NULL) {
        printf("该数据不存在!
");
        return root;
    }
    return DeleteNode(root, delNode);
}

void InOrderTraversal(rb_tree*node) {
    if(node != NULL) {
        InOrderTraversal(node->Left);
        printf("%d---%c
", node->val, ColorBoolean[node->Color]);
        InOrderTraversal(node->Right);
    }
}

void EraseTree(rb_tree*node) {
    if(node != NULL) {
        EraseTree(node->Left);
        EraseTree(node->Right);
        free(node);
        node = NULL;
    }
}

int main() {
    rb_tree*root, *x;
    ElemType Data;
    char ch;

    puts("1> 插入            2> 删除");
    puts("3> 查找            4> 显示");
    puts("5> 深度            6> 节点个数");
    puts("7> 黑高            8> 退出");

    x = root = Initialize();

    while((ch = getch()) != '8') {
        switch(ch) {
                case '1' :      printf("
插入数据:");
                                scanf("%d", &Data);
                                root = Insert(root, Data);
                        break;
                case '2' :      printf("
删除数据:");
                                scanf("%d", &Data);
                                root = Delete(root, Data);
                        break;
                case '3' :      printf("
查找数据:");
                                scanf("%d", &Data);
                                if((x = SearchNode(root, Data)) != NULL) {
                                    printf("%d %c
", x->val, ColorBoolean[x->Color]);
                                }
                                else
                                    printf("没有查找到数据!
");
                        break;
                case '4' :      printf("
显示数据:");
                                InOrderTraversal(root);
                                printf("
");
                        break;
                case '5' :      printf("
当前深度为:%d", Depth(root));
                        break;
                case '6' :      printf("
当前节点个数为:%d", Degree(root));
                        break;
                case '7' :      printf("
当前黑高为:%d", CurrentBlackHeight(root));
                        break;
            }
    }
    EraseTree(root);
    return 0;
}

　　插入的维护并不复杂，所以没什么好说的，改天加上配图再讨论一下，下面说说删除的维护。

　　实际上我在考虑要不要试试根据深度和节点颜色来实现删除的维护操作，emmm...但懒癌晚期，并不太想试。。。删除的维护操作想了一下午，但并没有找到很好的切入点。

　　进行删除的维护前，我们要弄清楚我们的目的：删除一个节点可能会破坏红黑树的性质，我们要维护被破坏的部分的性质。所以切入点很重要，删除掉的节点肯定没有了，我们不能通过它作为切入点，我们要找到一个比较合适的节点来检查红黑树的性质，这里检查实际上是隐式的，我们不会写明显的代码去检查红黑树的性质是否被破坏来进行维护。

　　合适的切入点一定选在删除节点的附近，或删除节点的父节点、或孩子节点，唯一的一种情况是删除节点的子树中的某个节点与其附近的节点。

　　我也是这样的思路，所以根据不同情况选择的有右孩子节点、父节点、右子树中恰比删除节点大的节点或其父节点、右孩子节点。

　　选择好这些节点后，我们才能开始进行维护，简单来说维护过程就是：检查该节点的位置、颜色情况根据可恢复性质的方法实现相对应的算法即可。但实际上要找到对几种情况通用的算法还是有点难的，不能把代码写死，还要能正确完成任务。

　　我被困住的部分是从如下图的基本情况：

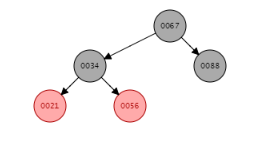
　　假如要删除67或者88，我们会先得到这样的：

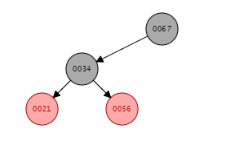
　　因为删除的是88，根据我的代码维护点为67，对于这种情况，我们只需要在67节点右旋一次即可，得到：

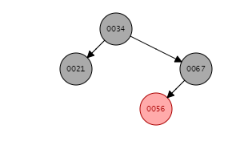
　　于是开始时设计的维护过程可能是这样：

if (node->Left != NULL) {
    node->Left->Color = RED;
    node->Color = BLACK;
    if (parent(node) != NULL)
        parent(node)->Color = RED;
    if (node->Left->Left != NULL)
        root = RightRotate(root, node);
    else
        root = LeftRightRotate(root, node);
    if (sibling(node) != NULL)
        sibling(node)->Color = node->Color;
}

　　但后面会发现还有许多坑...

　　突然懒得继续讨论了。。。

　　总之，慢慢来吧。。。

　　我发现自己越来越懒了 = =

　　然后说一说红黑树的平衡度，实际上红黑树不如AVL树平衡，假如一直往树的左（或右）子树中插入节点，到一定程度就会出现左边（或右边）更深的情况，但比普通的二叉树会好非常多，至少绝对不会出现左式树或右式树的情况，所以，整体的各种操作的时间复杂度为O(lg n)。为什么AVL树更平衡呢，因为AVL树可是依据各子树间的高度差来维护平衡的，且高度差不能超过2，条件很苛刻，所以比红黑树更平衡一点。

　　两张的红黑树：

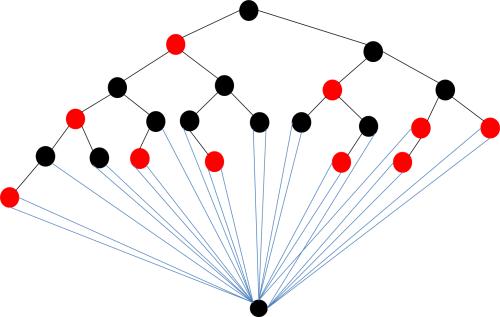
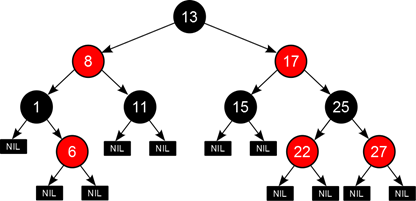
 　　　　　　　　　　　　图片来自网络

　　参考资料: wikipad-red black tree 、《算法导论》