以前对物理特别感兴趣的时候看过一段时间的变分法,记得当时阅读了一本十分不错的书籍,其作者名挺有趣的—老大中先生的《变分法基础》(真的很不错的一本讲变分法的书,有兴趣的同学可以去看看,虽然没继续看下去了> <),但许久没接触物理了,公式的推导过程也给忘记了,最近想复习一点数学、物理了,所以今天来推导一下并写篇博客做个记录。其实当时我的数学基础不足以支持我看完这本书...许多泛函的概念看的蒙蔽。。。但实际上直接去看最速降线问题的前面部分推导是没有太大影响的,基础只需要一点微积分+高中物理就能看明白原理...说起来当时仅仅是兴趣驱使我去深入了解什么是变分法...当时知道结论时非常激动。。。但如何解最后得到的公式才是真正的变分法基础。
首先来考虑一个问题:一个质点在重力作用下,从一个给定点到不在它垂直下方的另一点,如果不计摩擦力,问沿着什么曲线滑下所需时间最短?
问题稍微更物理一点的描述:设A、B是铅直平面上不在同一铅直线上的两点,在所有连接A和B的平面曲线中,求出一条曲线,使仅受重力作用且初速度为零的质点从A点到B点沿该曲线运动时所需时间最短。
如图所示(图来自百科):

下面是书上的证明:
如下图中所示,取A为平面直角坐标系的原点,x轴置于水平位置,y轴正向朝下。显然,最速降线应该在这个平面内。于是A点的坐标就是(0,0)。设B点的坐标为(x1,y1)。取连接A和B的曲线方程为:
$$ y = y(x) quad (0 leqslant x leqslant x_1) quad quad (1) $$
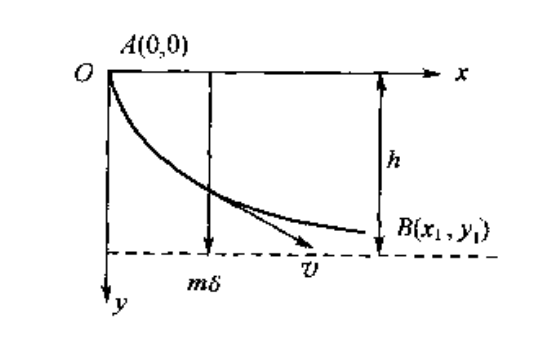
它在区间[0,x1]的两个端点满足条件:
$$ y(0) = 0,y(x_1)=y_1 quad quad (2) $$
设M(x,y)为曲线y=y(x)上的任意一点,由机械能守恒定律可得到如下关系:
$$ mgh + frac{1}{2}mv_0^2=mg(h-y) + frac{1}{2}mv^2 quad quad (3) $$
式中,v0=0,g是重力加速度,故有:
$$ v = sqrt{2gy} quad quad (4) $$
设y=y(x)为曲线的运动方程,质点沿着该曲线从A点运动到B点。质点的运动速度可表示为:
$$ v = frac{ds}{dt} = sqrt{1+y'^2} frac{dx}{dt} quad quad (5) $$
由式(4)、(5)消去v并积分,得质点沿曲线从A点滑行到B点所需的时间为:
$$ T=int_0^{x_1} sqrt{frac{1+y'^2}{2gy}}dx $$
该方程的最终解析式表示该问题的答案中的曲线是摆线(也叫滚轮线或旋轮线),非常让人一种着迷的曲线。但如何解这个方程我并不会...其涉及到求泛函问题的,使用的方法就是变分法,由于我太菜,基础知识储备不够,暂时还会解。。。
最后,说一点该问题的小故事:最早提出该问题的是伽利略。一开始伽利略猜测答案是圆,但没能证明,从现在来看是当然的,那时候微积分还没得到发展嘛...后来1696年约翰伯努利在一封写给他哥哥雅克比伯努利(向伯努利家族低头orz)公开信中再次提出该问题,引起当时的数学家们的热议和研究,我个人听说实际上是专门向牛顿提出的挑战,考验牛顿的微积分水平。。。结果当时牛顿收到消息时已经过了大半年,但牛顿立刻就回家开始研究,花了一下午解决了问题,虽然消息来得晚,但牛顿却是提出问题后第一个解决该问题的orz。。。后来陆陆续续有一些著名的数学家都证明出来了,其中有莱布尼茨、洛必达等。这个问题标志着变分法基础的开始,后来该问题得到了欧拉、拉格朗日等著名的数学家的工作,发展出了变分法这门学科。
其他参考文献:
1.https://en.wikipedia.org/wiki/Brachistochrone_curve
2.https://en.wikipedia.org/wiki/Calculus_of_variations
3.https://baike.baidu.com/item/%E5%8F%98%E5%88%86%E6%B3%95/83603?fr=aladdin
4.https://baike.baidu.com/item/%E6%91%86%E7%BA%BF/5893005?fr=aladdin
5.https://baike.baidu.com/item/%E6%B5%8B%E5%9C%B0%E7%BA%BF/2391217?fr=aladdin