Voronoi图和Delaunay三角剖分

刷题的时候发现了这么一个新的东西：Voronoi图和Delaunay三角剖分

发现这个东西可以$O(nlogn)$解决平面图最小生成树问题感觉非常棒

然后就去学了..

看的n+e的blog，感谢n+e的耐心教导..

---

Voronoi图是个啥

百度百科

---

Delaunay三角剖分

最优三角剖分就是使每一个三角形的外接圆都不包含其他的点的三角剖分

这个算法就是求最优三角剖分的

简单来说就是分治合并

非常详细的一篇文章

对于点数小于等于$3$的可以直接连边

合并的时候

1）先找到两边最下面的点，这个可以用凸包求，然后连边

2）对于现在得到的两个点$p_1$、$p_2$，找到一个点连接着$p_1$且由这三个点的外接圆不包含别的任何点，并删除这个外接圆经过的边，$p_2$也是如此

3）看现在找出来的两个点$y_1$、$y_2$，找其中一个点使得它与$p_1$、$p_2$的外接圆不包含另外一个点，使其与对应的点连边

4）重复（2）（3）直到无边可连

---

对n+e代码的修改

一开始压根不知道怎么实现这个算法的时候去看了看n+e的代码..

发现他的代码中每次都要遍历$p_1$和$p_2$的所有边，这样的做法在特殊的图里面是$O(n^2)$的

可以说他自己出的数据偏水？？（雾

然后看了上面那篇详细的文章，发现它的边是按照顺时针或者逆时针的方向进行取边的，这样遇到的边要不删掉要不就是最优的

所以我开了一个双向链表来储存边，使得边是按照$(-dfrac{pi}{2},dfrac{3pi}{2}]$顺时针排列

然后就会发现细节一大堆..

调了我3天的东西就直接放上来好了

---

判断一个点是否在某三个点的外接圆内

在这篇blog里面有讲，但是貌似图都爆掉了？？

就是把点映射到$z=x^2+y^2$的抛物面上，这三个点就会形成一个新的平面，然后再判断剩下的那个点和这个平面的关系即可

下面放几张n+e给我的图片方便理解？

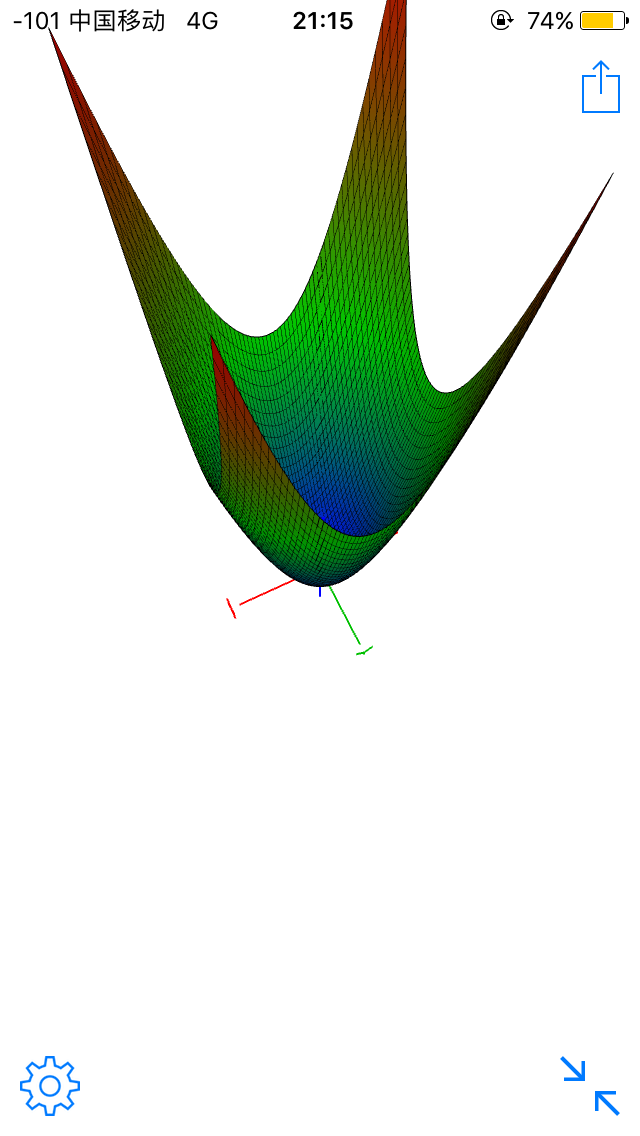
抛物面$z=x^2+y^2$

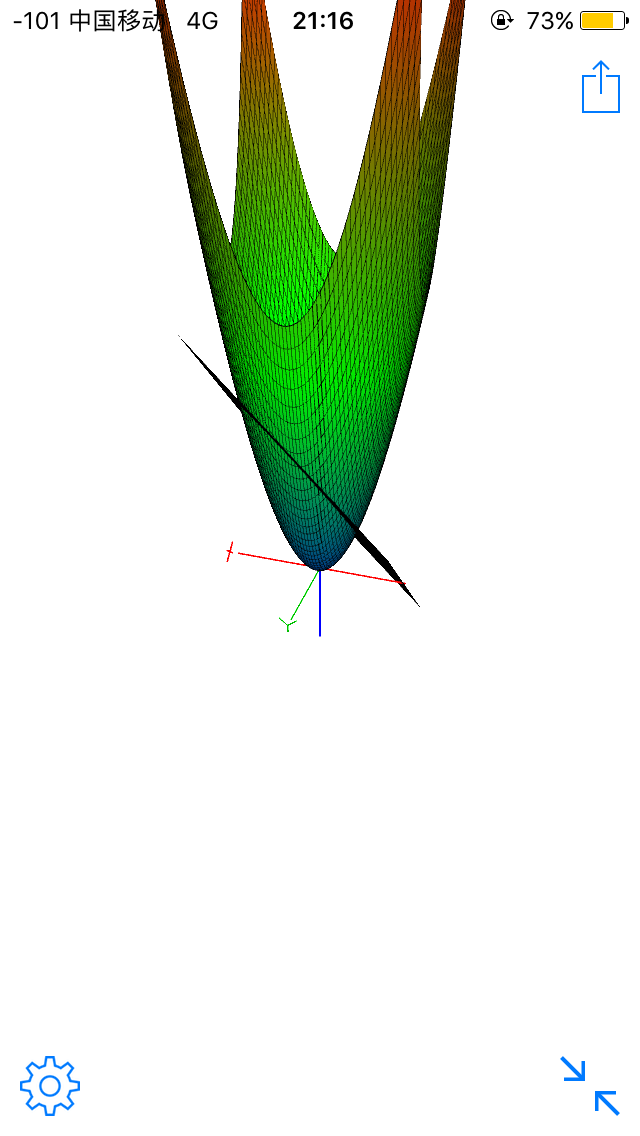
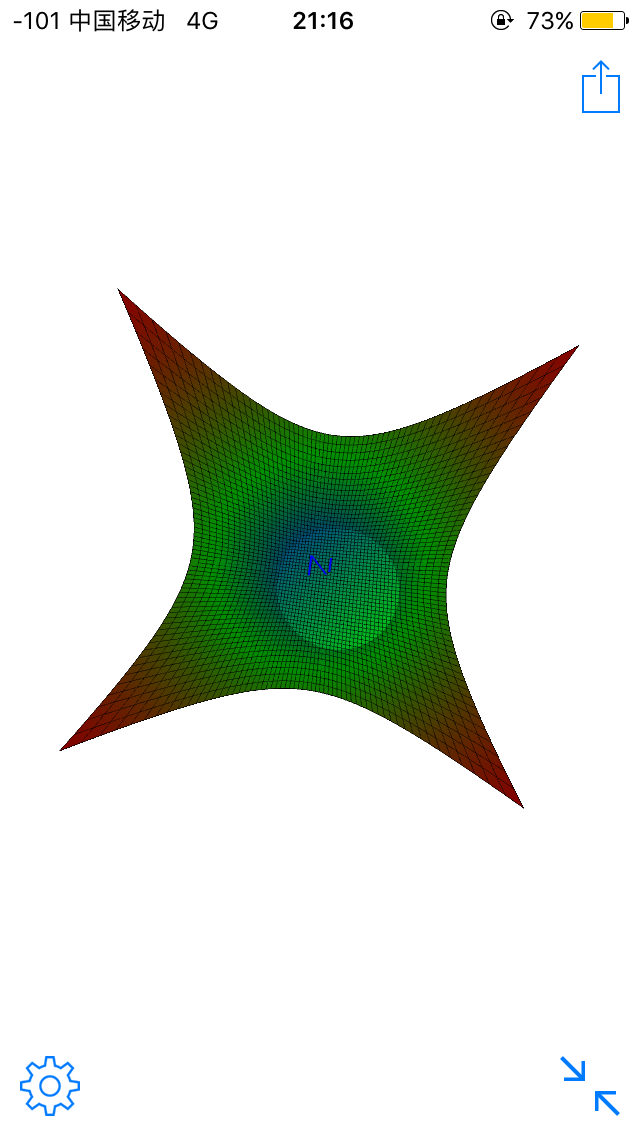
其实第三张图应该很清晰了吧..

在圆内的点都会在平面下方，而在圆外的都会在平面上方

这个用三维叉积点积判一下就好了

---

Code

下面就贴一下我3天的成果吧..

还有什么问题请指教..

bzoj4219

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <vector>
#define eps 1e-10
using namespace std;
const int Maxn = 100010;
double _max(double x, double y) { return x > y ? x : y; }
double _min(double x, double y) { return x < y ? x : y; }
struct node {
	int y, nxt, frt, opp;
}a[Maxn<<3]; int first[Maxn], last[Maxn], num[Maxn<<3], now;
int sta[Maxn], tp;
int pb(int x, int k, int y) {
	int u = num[now++];
	a[u].y = y; a[u].frt = k;
	if(k){
		a[u].nxt = a[k].nxt;
		if(a[k].nxt) a[a[k].nxt].frt = u;
		else last[x] = u;
		a[k].nxt = u;
	} else {
		if(first[x]) a[first[x]].frt = u;
		else last[x] = u;
		a[u].nxt = first[x]; first[x] = u;
	}
	return u;
}
int pf(int x, int k, int y) {
	int u = num[now++];
	a[u].y = y; a[u].nxt = k;
	if(k){
		a[u].frt = a[k].frt;
		if(a[k].frt) a[a[k].frt].nxt = u;
		else first[x] = u;
		a[k].frt = u;
	} else {
		if(last[x]) a[last[x]].nxt = u;
		else first[x] = u;
		a[u].frt = last[x]; last[x] = u;
	}
	return u;
}
void del(int x, int k) {
	num[--now] = k;
	if(a[k].nxt) a[a[k].nxt].frt = a[k].frt;
	else last[x] = a[k].frt;
	if(a[k].frt) a[a[k].frt].nxt = a[k].nxt;
	else first[x] = a[k].nxt;
}
double _abs(double x) { return x < 0 ? -x : x; }
int zero(double x) { return _abs(x) < eps ? 1 : 0; }
struct Point {
	double x, y;
	Point(double x = 0, double y = 0) : x(x), y(y) {}
	bool operator<(const Point &A) const { return zero(x-A.x) ? y < A.y : x < A.x; }
	Point operator-(const Point &A) const { return Point(x-A.x, y-A.y); }
}list[Maxn]; int n; double X, Y;
double Cross(Point A, Point B) { return A.x*B.y-B.x*A.y; }
double Dot(Point A, Point B) { return A.x*B.x+A.y*B.y; }
double dis(Point A) { return sqrt(Dot(A, A)); }
double dis(int x, int y) { return dis(list[y]-list[x]); }
struct Point3 {
	double x, y, z;
	Point3(double x = 0, double y = 0, double z = 0) : x(x), y(y), z(z) {}
	Point3 operator-(const Point3 &A) const { return Point3(x-A.x, y-A.y, z-A.z); }
};
double Dot(Point3 A, Point3 B) { return A.x*B.x+A.y*B.y+A.z*B.z; }
Point3 Cross(Point3 A, Point3 B) { return Point3(A.y*B.z-A.z*B.y, A.z*B.x-A.x*B.z, A.x*B.y-A.y*B.x); }
Point3 t(Point A) { return Point3(A.x, A.y, A.x*A.x+A.y*A.y); }
bool incir(Point D, Point A, Point B, Point C) {
	if(Cross(B-A, C-A) < -eps) swap(B, C);
	Point3 aa = t(A), bb = t(B), cc = t(C), dd = t(D);
	return Dot(Cross(bb-aa, cc-aa), dd-aa) < -eps;
}
bool incir(int D, int A, int B, int C) { return incir(list[D], list[A], list[B], list[C]); }
void divi(int L, int R) {
	if(L == R) return;
	if(L+1 == R){
		int k1 = pb(L, 0, R); int k2 = pf(R, 0, L);
		a[k1].opp = k2; a[k2].opp = k1;
		return;
	}
	int mid = L+R>>1, i, j, k;
	divi(L, mid); divi(mid+1, R);
	int p1 = 0, p2 = 0; tp = 0;
	for(i = L; i <= R; i++){
		while(tp > 1 && Cross(list[i]-list[sta[tp-1]], list[sta[tp]]-list[sta[tp-1]]) > eps) tp--;
		sta[++tp] = i;
	}
	for(i = 1; i < tp; i++) if(sta[i] <= mid && sta[i+1] > mid){ p1 = sta[i]; p2 = sta[i+1]; break; }
	int kp1, kp2;
	for(kp1 = last[p1]; kp1; kp1 = a[kp1].frt){
		if(Cross(list[a[kp1].y]-list[p1], list[p2]-list[p1]) < eps || Cross(list[a[kp1].y]-list[p1], Point(0,1)) < -eps) break;
	}
	int k1 = pb(p1, kp1, p2);
	for(kp2 = first[p2]; kp2; kp2 = a[kp2].nxt){
		if(Cross(list[a[kp2].y]-list[p2], list[p1]-list[p2]) > -eps || Cross(list[a[kp2].y]-list[p2], Point(0,1)) > eps) break;
	}
	int k2 = pf(p2, kp2, p1);
	a[k1].opp = k2; a[k2].opp = k1;
	while(1){
		int np1 = 0, np2 = 0;
		for(; kp1; kp1 = a[kp1].frt){
			if(Cross(list[a[kp1].y]-list[p1], list[p2]-list[p1]) > -eps){
				if(Cross(list[a[kp1].y]-list[p1], Point(0,1)) > -eps) continue;
				else break;
			}
			if(a[kp1].frt && incir(a[a[kp1].frt].y, p1, p2, a[kp1].y)) del(a[kp1].y, a[kp1].opp), del(p1, kp1);
			else { np1 = kp1; break; }
		}
		for(; kp2; kp2 = a[kp2].nxt){
			if(Cross(list[a[kp2].y]-list[p2], list[p1]-list[p2]) < eps){
				if(Cross(list[a[kp2].y]-list[p2], Point(0,1)) < -eps) continue;
				else break;
			}
			if(a[kp2].nxt && incir(a[a[kp2].nxt].y, p1, p2, a[kp2].y)) del(a[kp2].y, a[kp2].opp), del(p2, kp2);
			else { np2 = kp2; break; }
		}
		if(!np1 && !np2) break;
		if(!np2 || (np1 && !incir(a[kp2].y, p1, p2, a[kp1].y))){
			p1 = a[kp1].y;
			k2 = pf(p2, kp2, p1);
			for(kp1 = last[p1]; kp1; kp1 = a[kp1].frt){
				if(Cross(list[a[kp1].y]-list[p1], list[p2]-list[p1]) < eps || Cross(list[a[kp1].y]-list[p1], Point(0,1)) < -eps) break;
			}
			k1 = pb(p1, kp1, p2);
			a[k1].opp = k2; a[k2].opp = k1;
		} else {
			p2 = a[kp2].y;
			k1 = pb(p1, kp1, p2);
			for(kp2 = first[p2]; kp2; kp2 = a[kp2].nxt){
				if(Cross(list[a[kp2].y]-list[p2], list[p1]-list[p2]) > -eps || Cross(list[a[kp2].y]-list[p2], Point(0,1)) > eps) break;
			}
			k2 = pf(p2, kp2, p1);
			a[k1].opp = k2; a[k2].opp = k1;
		}
	}
}
struct enode {
	int x, y; double d;
	enode(int x = 0, int y = 0, double d = 0) : x(x), y(y), d(d) {}
	bool operator<(const enode &A) const { return d < A.d; }
}e[Maxn<<4]; int el;
int fa[Maxn];
int ff(int x) { return fa[x] == x ? x : fa[x] = ff(fa[x]); }
int main() {
	int i, j, k;
	scanf("%d%lf%lf", &n, &X, &Y);
	for(i = 1; i <= n; i++) scanf("%lf%lf", &list[i].x, &list[i].y);
	now = 1;
	for(i = 1; i <= n<<3; i++) num[i] = i;
	sort(list+1, list+n+1);
	divi(1, n);
	for(i = 1; i <= n; i++){
		e[++el] = enode(i, n+1, _min(list[i].x, Y-list[i].y));
		e[++el] = enode(i, n+2, _min(list[i].y, X-list[i].x));
		for(k = first[i]; k; k = a[k].nxt) e[++el] = enode(i, a[k].y, dis(i, a[k].y)/2.0);
	}
	sort(e+1, e+el+1);
	for(i = 1; i <= n+2; i++) fa[i] = i;
	for(i = 1; i <= el; i++){
		int fx = ff(e[i].x), fy = ff(e[i].y);
		if(fx != fy){
			fa[fx] = fy;
			if(ff(n+1) == ff(n+2)){ printf("%lf
", e[i].d); return 0; }
		}
	}
	return 0;
}

---

小总结？？

虽然这次搞这个东西用的时间很长.. 但是收获还是很大的..

最后差那么几个点wa还是很想放弃的..

但是还是坚持下了来了嘛..

加油啊..