题目描述:
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
输入参数:target(查找值) array(二维数组)
解题思路:
1、python代码
python实现比较简单,使用for in循环取出数组的每行i,然后使用in操作符判断target是否在行i中
1 # -*- coding:utf-8 -*-
2 class Solution:
3 # array 二维列表
4 def Find(self, target, array):
5 # write code here
6 for i in array:
7 if target in i:
8 return True
9 return False
2、java代码
我们先看一个符合题目要求的数组
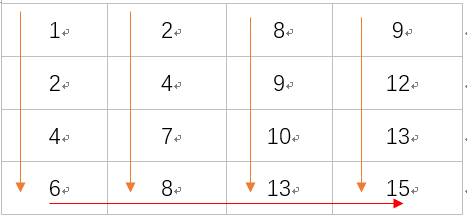
数组特点:每行元素满足从左向右增大,每列元素满足自上而下增大
同行不同列的数值存在确定的大小关系,同列不同行的数值存在确定的大小关系,数值减小的方向为:向上或向左(数值增大的方向:向下或向右)
需要注意,不同行不同列的数据间并无确定的大小关系。例如:a[1][0]>a[0][0],但是a[1][0]<a[0][2]。
考虑到数组的最后一行每个元素均为所在列的最大值,如果其小于要搜索的值,那可以直接忽略该列及其之前列的所有元素。
算法(递归):
m:行数 n:列数
(1)遍历最后一行(rowindex=m-1),找到第一个大于target的元素,存储其列索引colindex
(2)向上搜索:find(rowindex,colindex,"up",target,array)
(2)递归
a.当前操作为向上搜索(direction='up'):
如果rowindex==0:已经搜索至第一行,无解,返回false
否则,rowindex-=1
b.当前操作为向右搜索(direction='right'):
如果colindex==n-1:已经搜索至最后一列,无解,返回false
否则,colindex+=1
a.如果array[rowindex][colindex]==target:返回true
b.如果array[rowindex][colindex]>target:向上搜索find(rowindex,colindex,"up",target,array)
c.如果array[rowindex][colindex]<target:向右搜索find(rowindex,colindex,"right",target,array)
按照如上算法和数组,举例说明,搜索元素12步骤如下:
(1)m=4,n=4.最后一行第一个大于12的元素为13,存储其行列索引,rowindex=3,colindex=2
(根据数值大小排列的特点,可以排除掉第一列和第二列的所有元素)
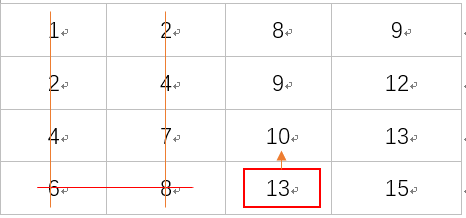
(2)向上搜索:find(rowindex=3,colindex=2,direction="up",target=11,array)
(3)递归:
向上搜索:rowindex=2,colindex=2,10<12:向右搜索
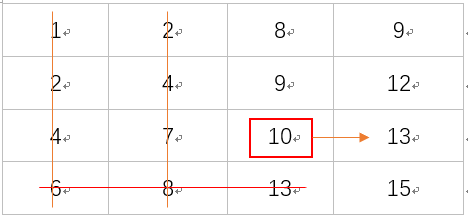
向右搜索:rowindex=2,colindex=3,13>12:向上搜索
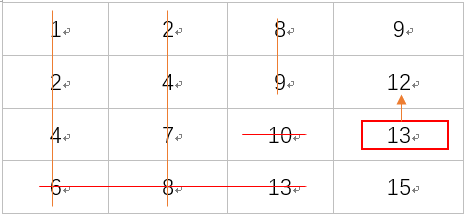
向上搜索:rowindex=1,colindex=3,12=12:停止搜索,返回true
代码如下:
1 public class Solution {
2 public boolean Find(int target, int [][] array) {
3 int m=array.length;
4 int n=array[0].length;
5 int colindex=-1;
6 int rowindex=m-1;
7 for(int i=0;i<n;i++){
8 if(array[m-1][i]>target){
9 colindex=i;
10 break;
11 }
12 else if (array[m-1][i]==target){
13 return true;
14 }
15 }
16 if(colindex==-1){
17 return false;
18 }
19 else{
20 return find(rowindex,colindex,"up",target,array);
21 }
22 }
23
24 public boolean find(int rowindex,int colindex,String direction,int target, int [][] array){
25 if(direction=="up"){
26 if(rowindex==0){
27 return false;
28 }
29 else{
30 rowindex--;
31 }
32 }
33 else if(direction=="right"){
34 if(colindex==array[0].length-1){
35 return false;
36 }
37 else{
38 colindex++;
39 }
40 }
41 if(array[rowindex][colindex]<target){
42 return find(rowindex,colindex,"right",target,array);
43 }
44 else if(array[rowindex][colindex]>target){
45 return find(rowindex,colindex,"up",target,array);
46 }
47 else{
48 return true;
49 }
50 }
51 //测试代码
52 // public static void main(String[]args){
53 // int array1[][]={{1,2,8,9},{2,4,9,12},{4,7,10,13},{6,8,11,15}};
54 // Solution sol=new Solution();
55 // boolean a=sol.Find(14,array1);
56 // System.out.println(a);
57 // }
58 }