树状数组--二叉索引树

突然发现

自己好久好久没写博客了

大概是最近要做的题太多了吧

而在写这篇之前

我还犹豫了好久

自己思索好大一番为什么要写博

差点放弃的时候

我终于找的一个小小的理由

我记性实在是太差了

而翻书，上网查有一点点绕弯路

所以

我坚持了

-------------------------------------------------

不得不说

我的知识点漏洞太大了

一方面是我记性不好

一方面是我太懒了

（一定要改啊啊！！）

蒟蒻的卑微

----------------------------------------------

那么

进入正题

---------------------------------------------

动态连续和查询问题。

给定一个n个元素的数组A1、A2、...,An,我们的任务是设计一个数据结构，支持以下两种操作。

***　　add（x，d）操作：让Ax增加d。

***　　Query（L,R）：计算A_L+A_L+1+...A_R。

为了更快的操作（为了不tle）

用一种称为二叉索引树（BIT）的数据结构

****************************************************************************************************************

前置知识：

lowbit

对于一个正整数x，我们定义lowbit（x）为x的二进制表达式中最右边的1所对应的值

eg.38288 的二进制是 1001010110010000 所以lowbit（38288） = 16（16的二进制是10000）

在程序实现中：

　　　　lowbit（x） = x &（-x）;

（-x是x按位取反，末尾加1的结果）

 38288 = 1001010110010000

-38288 = 0110101001110000

两者按位“与”后，前面的部分全变0，之后（后5位）lowbit保持不变

*******************************************************************************************************************

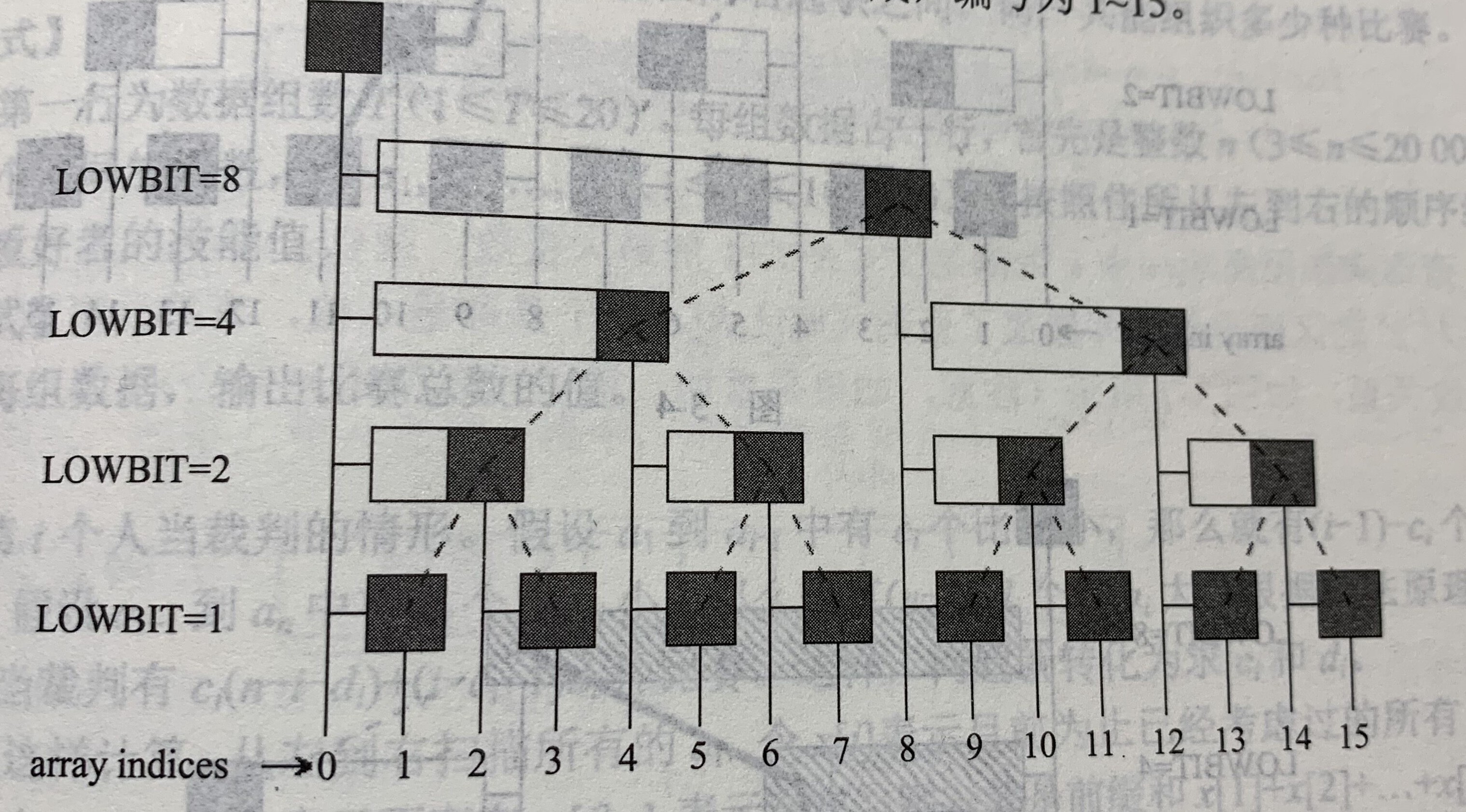
灰色结点点是BIT中的结点（白条一会儿再说）

每一层结点的lowbit相同

而且lowbit越大越靠近根

注意：
　　编号为0的点是虚拟结点，并不是树的一部分，但是，它的存在会让算法更容易理解。

对于结点i:

　　若为左子结点：他的父结点编号为i + lowbit（i）；

　　若为右子结点：他的父结点编号为i - lowbit（i）；

（应该不用证明，直观感受它的正确性，并记住这个性质就好）

构造一个辅助数组C：

　　C_i=A_{i-lowbit(i)+1} + A_{i-lowbit(i)+2}+...+A_i

C的每个元素都是A数组中的一段连续和。

在BIT中每个灰色结点i都属于一个以它自身为结尾的水平长条

（lowbit = 1的那些点，“长条”就是那个结点自己）

这个长条中的数之和就是C_i。

eg.结点12的长条就是从9~12，即C₁₂=A₉+A₁₀+A₁₁+A₁₂

eg.C₆=A₅+A₆

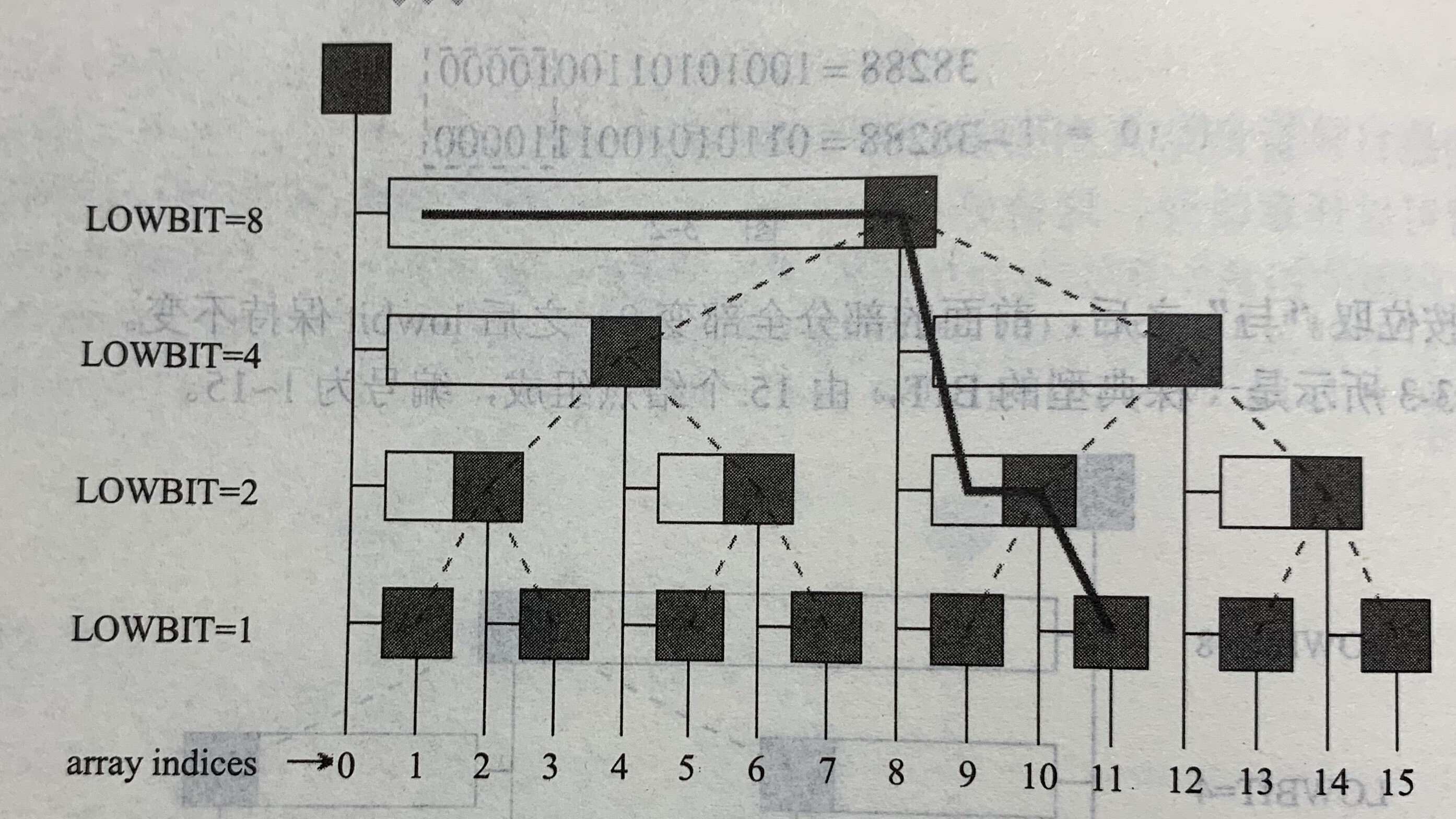
Query（L,R）-----------求和

顺着结点i往左走，边走边“往上爬”（不一定沿着树中的边爬）

把沿途经过的C_i累加起来就可以啦

（沿途经过的Ci所对应的长条不重复也不遗漏的包含了所有需要累加的元素）

int sum(int x)
{
    int ret = 0;
    while(x > 0)
    {
        ret += C[x];
        x -= lowbit(x);
    }
    return ret;
} 

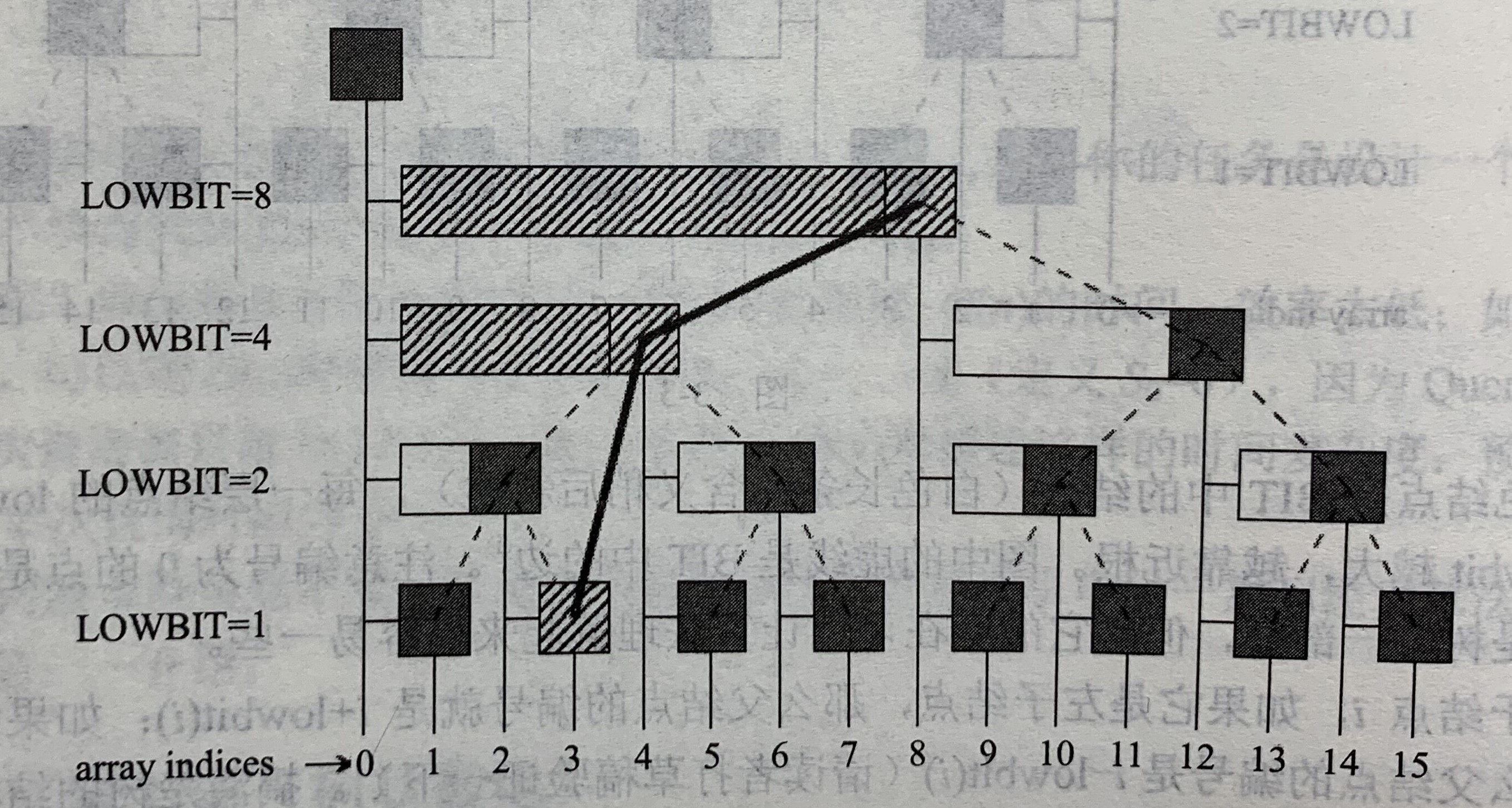
add（x，d）----------增加

从C_i开始往右走，边走边“往上爬”（同样，不一定沿着树中的边爬）

沿途修改所有结点的Ci即可（有且仅有这些结点对应的长条包含被修改的元素）

void add(int x,int d)
{
    while(x <= n)
    {
        C[x] += d;
        x +=lowbit(x);
    }
}

两个时间复杂度均为O（nlogn）