description:

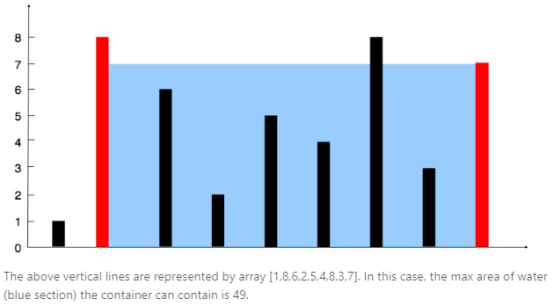
| Input: [1,8,6,2,5,4,8,3,7]Output: 49 |
思路1:
从(1,a1)开始向后算面积,需要两层n循环,时间复杂度n2
思路2:
找出数组中最大的数,将其与次大,第三大数求面积,依次类推,也需要两层循环,还需要额外排序,时间复杂度n2
因为找出最大数并且并不知道输入数据的规律(有可能很杂乱),所以每个都有必要算,采取思路1.
代码实现如下:
class Solution { public int maxArea(int[] height) { int max = 0; for(int i = 0; i < height.length; i++){ int mid = maxSpare(height, i); max = max >= mid ? max : mid; } return max; } // 从index = start开始向后对每一对求面积 private int maxSpare(int[] height, int start){ int maxArea = 0; for(int i = start + 1; i < height.length; i++){ int area = countArea(height[start], height[i], i - start); maxArea = maxArea > area ? maxArea : area; } return maxArea; } private int countArea(int height1, int height2, int width){ int result = 0; int height = height1 > height2 ? height2 : height1; result = height * width; return result; } }
|
but only faster 15.40% of Java online submissions for Container With Most Water. |
讨论区看见O(n)的算法:
|
(1)left = 0, right = n-1,计算left~right之间的面积 (2)若left的高度小于right的高度,则查找2~n-1之间大于left的位置,更新left,计算面积;否则,查找中间大于right高度的位置,作为新right,计算面积 (3)直到right< left |
思考:
设以left=1为基点不变,找到一个right值,使left~right之间的矩形面积最大,则存在以下三种情况:
①aleft > aright

此时高度height=aright,width=(n-1),所求面积可能小于等于以a1为左边的最大面积。
②aright为右边起第一个大于等于aleft的边,设right=n-1

此时height=aleft,width= (n-1)-1,面积有可能等于为以a1为左边的最大面积。
③aright不为右边起第一个大于等于aleft的边,设right=n-2
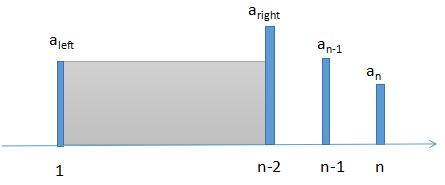
此时虽然height=aleft,但是width=(n-2)-1小于②中的width,所以③中求得的面积小于②中的面积,即③中的情况是不考虑的。
所以可以两头推进。参考如下代码:
class Solution { public int maxArea(int[] height) { int max = 0, left = 0, right = height.length-1; while(left < right){ int area = Math.min(height[left],height[right]) * (right - left); max = max > area ? max : area; if(height[left] < height[right]){ int base = height[left]; while((height[left] <= base) && (left < right)){ left++; } // end while } else{ int base = height[right]; while((height[right] <= base) && (left < right)){ right--; } // end right } // end if-else } // end while return max; } // end maxArea }
| Runtime: 7 ms, faster than 55.28% of Java online submissions for Container With Most Water. |
算法很重要
一个3ms的代码:
class Solution { public int maxArea(int[] height) { int maxarea = 0; int temparea = 0; int i = 0; int j = height.length -1; while(i < j) { if(height[i] <= height[j]) { temparea = height[i] * (j-i); i++; } else { temparea = height[j] * (j-i); j--; } if(temparea > maxarea) { maxarea = temparea; } } return maxarea; }
}