实验名称
回溯法解N皇后问题
实验目的
- 掌握回溯递归算法、迭代算法的设计与实现;
- 设计回溯算法求解;
- 分析算法的时间复杂度。
实验环境
操作系统:win 10;
编程语言:Java;
开发工具:IDEA;
问题描述
在n×n格的国际象棋上摆放n个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法?

实验过程
回溯法
按照优先级条件向前搜索以达到目标。但是当探索到某一步时,发现原先选择并不能达到目标,就退回上一步重新选择,这种走不通就退回的技术叫做回溯。
问题解决思路
用数组模拟棋盘,从第一行开始,依次选择位置,如果当前位置满足条件,则向下选择位置,如果不满足条件,那么当前位置向后移动一位。
最后一个不满足,回溯到上一行,选择下一个位置继续进行探索。
其实并不需要一个n*n的数组,我们只需要一个长度为n的数组来存储位置,array[i] = k;表示第i行,第k个位置放皇后。
解题步骤
1. 因为皇后之间不能放在同一行,同一列,同一斜线。所以每行放一个皇后,就解决了不在同一行的问题。result[row]=j;表示第row行,第j列放置皇后。
2. 在第i行的时候,遍历n列,试探位置,和之前所有行放的位置进行比较。
3. 判断当前位置是否可以放皇后:如果当前列和之前皇后所在的列相等即result[i] == col 或者在同一个斜线上: result[i] == col - sub || result[i] == col + sub;代表当前位置不合法,返回false,如果当前位置可以放置皇后,那就将这个位置的坐标记录下来result[row] = j;j代表的是皇后所在的列;
4. 回溯,然后在下一行寻找皇后放置的位置。
代码实现
1. package org.qianyan.algorithm;
2.
3. import java.util.ArrayList;
4. import java.util.Arrays;
5. import java.util.List;
6.
7. /**
8. * @Author Huhuitao
9. * @Date 2020/12/17 15:51
10. */
11. public class NQueens {
12. public static void main(String[] args) {
13. NQueens nQueens = new NQueens();
14. long begin_time = System.currentTimeMillis();
15. int N = 8;
16. List<List<String>> lists = nQueens.solveNQueens(N);
17. long end_time = System.currentTimeMillis();
18. System.out.println(end_time - begin_time + "ms");
19. lists.stream().forEach(list -> {
20. System.out.println("==========================");
21. for (int i = 0; i < list.size(); i++) {
22. System.out.println(list.get(i));
23. }
24. });
25. System.out.println("==========================");
26. System.out.println(N+"皇后,有"+lists.size()+"种解决方案");
27. }
28.
29. private List<List<String>> results = new ArrayList<>(); // 结果集
30.
31. public List<List<String>> solveNQueens(int n) {
32. int[] result = new int[n]; // 记录每一行皇后放置的 列坐标
33. backtracking(result, 0);
34. return results;
35. }
36.
37. /**
38. * 回溯
39. *
40. * @param result
41. * @param row
42. */
43. private void backtracking(int[] result, int row) {
44. if (row == result.length) {
45. //递归结束条件,放置完成最后一行,将结果添加到results
46. List<String> temp = new ArrayList<>();
47. for (int i = 0; i < result.length; i++) {
48. char[] str = new char[row];
49. Arrays.fill(str, '.');
50. str[result[i]] = 'Q';
51. temp.add(new String(str)); // 根据每一行出现皇后的位置填充解
52. }
53. results.add(temp); // 加入当前解
54.
55. }
56. for (int j = 0; j < result.length; j++) {
57. //如果这个位置能放置皇后
58. if (isValidation(result, row, j)) {
59. //记录放置坐标
60. result[row] = j;
61. //放置下一行
62. backtracking(result, row + 1);
63. }
64. }
65.
66. }
67.
68. // 验证,无同行/同列棋子
69. // 对角线无棋子
70. private boolean isValidation(int[] result, int row, int col) {
71. for (int i = 0; i < row; i++) { // 第一行可以放任意位置
72. int sub = row - i; // 行数差
73. // 如果同列、同对角线出现皇后,说明不能在row col放置皇后
74. if (result[i] == col || result[i] == col - sub || result[i] == col + sub) {
75. return false;
76. }
77. }
78. //检测结束后能放置
79. return true;
80. }
输出结果
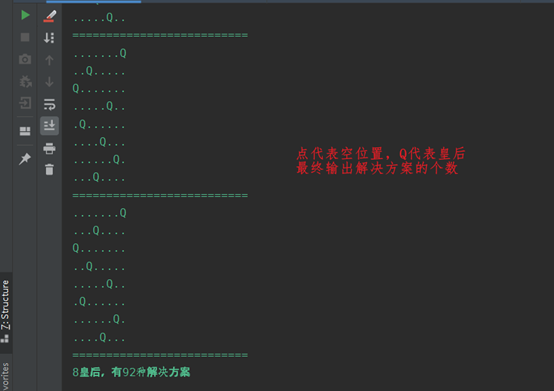
算法分析
N 皇后问题的解空间是一棵n叉树,树的深度是n,最坏情况下解空间树深度是n,除了根节点和叶子结点,其余结点的子节点有n个分支,总分枝的个数是nn,每个分支都判断约束函数,判断约束条件需要O(n)的时间,因此耗时需要O(n(n+1)),所以时间复杂度是O(n^(n+1));
回溯法的另一个重要特性是在搜索执行的同时产生解空间,从开始结点起最长的路径是n,我们声明的result数组大小是n,用来保存皇后的坐标。所以该算法的空间复杂度是O(n)。
回溯法算是一种选优搜索法,按照选优条件深度优先搜索,达到目标,当搜索到某一步时,发现原先选择不是目标或者不是最优就退回重新选择。这种方法通过剪枝来减少递归的次数。如果超时的话可以换其他方法解决。