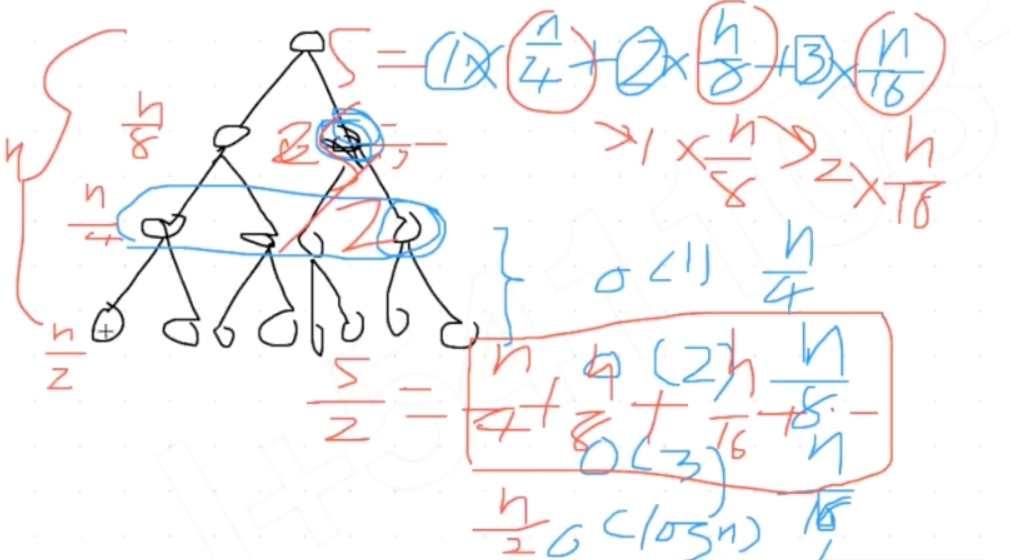
heapify unsorted array: n*logn -> o(n): 最贵的 o(logn) 操作集中在少数几个node 上
heapify: 从下往上,从右往左, 从第一个internal node 开始往下 PUSH
8 (2)
/
5 4 (2) (8) (4)
/ /
6 7 9 2 (4) (8)
4->2 8->2 8->4 : 堆序性 时间复杂度 O(N)
但heapify 并不是 sort, 左右并没有排序,如果需要排序的话,需要先heapify 然后再 一个一个的poll 时间复杂度是 on + onlogn = onlogn

1 public class MyPriorityQueue {
2 /*
3 Heap: 不管谁先进去,最小的先出来 实现通过 PriorityQueue
4 binary heap: 堆序性 满树性 所有ITEM 的 REF 存在一个数组里, OBJECT 分散存的
5 offer: 加入气泡位置满足满树性,然后往上一层的NODE翻 满足堆序性 o(LOGN)
6 peek: 每次操作堆顶元素 o(1)
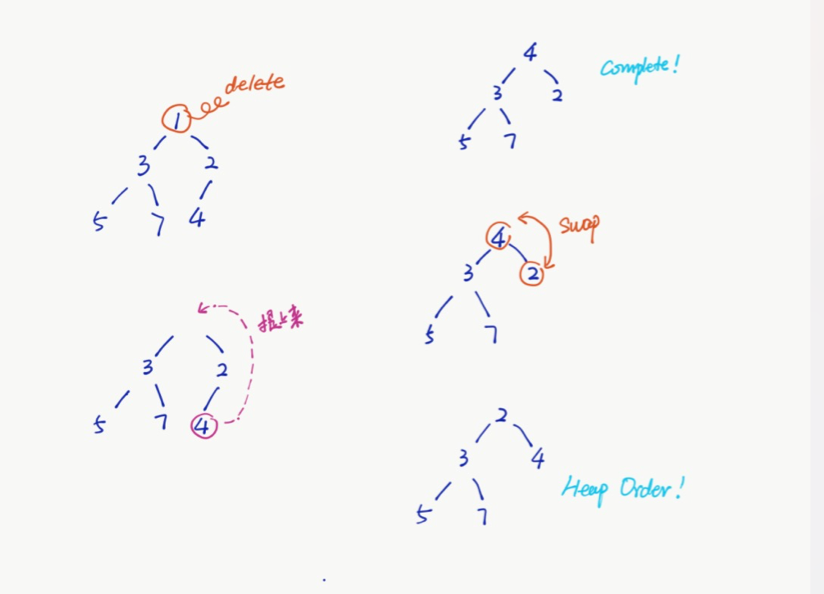
7 poll: 1: 删除堆顶元素-1,2)把最后一个元素 4 放入堆顶-满足满树的性质, 3) 然后和左右比较大小往下PUSH-调整堆序性质 2 和 4 互换位置 o(LOGN)
8 1
9 /
10 3 2
11 / /
12 5 7 4
13
14 poll peek size isEmpty()
15 * */
16 public static void main(String[] args) {
17 Queue<Integer> pq = new PriorityQueue<>() ;
18 pq.offer(3);
19 pq.offer(1);
20 pq.offer(2);
21 System.out.println(pq.poll());//1
22 System.out.println(pq.poll()); //2
23
24 }
25
26 /*
27 https://stackoverflow.com/questions/1871253/updating-java-priorityqueue-when-its-elements-change-priority
28 You have to remove and re-insert, as the queue works by putting new elements in the appropriate position when they are inserted
29 * */
30 @Test
31 public void pqUpdate_wrong(){
32 //have to pass in comparator, otherwise the pq dont know how to order node obj.
33 Queue<Node> pq = new PriorityQueue<>(new MyComparator()) ;
34 Node n1 = new Node(3) ;
35 Node n2 = new Node(1);
36 Node n3 = new Node(2);
37 pq.offer(n1);
38 pq.offer(n2);
39 pq.offer(n3);
40 n2.val = 100 ;
41 System.out.println(pq.poll().val); //100: the ref order stays the same
42 //pq只在 OFFER 的时候才会更新顺序
43 }
44
45 @Test
46 public void pqUpdate_correct(){
47 //have to pass in comparator, otherwise the pq dont know how to order node obj.
48 Queue<Node> pq = new PriorityQueue<>(new MyComparator()) ;
49 Node n1 = new Node(3) ;
50 Node n2 = new Node(1);
51 Node n3 = new Node(2);
52 pq.offer(n1);
53 pq.offer(n2);
54 pq.offer(n3);
55 n2.val = 100 ; //o(1)
56 pq.remove(n2);//remove 的时间复杂度是 o(n): binary heap 是无序 所以需要遍历来寻找, 找到之后 POLL 然后堆序性 O(LOGN): O(N)+O(LOGN) =O(N)
57 pq.offer(n2) ;//o(logn)
58 System.out.println(pq.poll().val);//2
59 }
60
61 /*
62 heapify: 从下往上,从右往左, 从第一个internal node 开始往下 PUSH
63
64 8 (2)
65 /
66 5 4 (2) (8) (4)
67 / /
68 6 7 9 2 (4) (8)
69
70 4->2 8->2 8->4 : 堆序性 时间复杂度 O(N)
71 * */
72 }
73
74 class Node{
75 int val ;
76 public Node(int val) {
77 this.val = val;
78 }
79 }
80
81 class MyComparator implements Comparator<Node>{
82 @Override
83 public int compare(Node n1, Node n2) {
84 if (n1.val<n2.val){
85 return -1 ;
86 } else if(n1.val == n2.val){
87 return 0;
88 } else {
89 return 1 ;
90 }
91 //the following could result Integer overflow
92 //return n1.val - n2.val ;
93 }
94 }
Priority Queue 时间复杂度分析:

.offer:
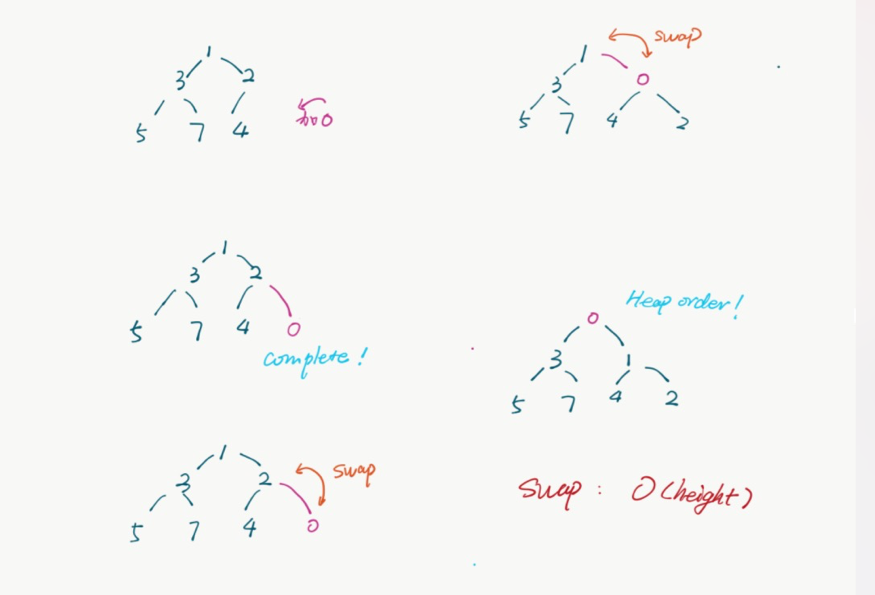
.offer: