0654最大二叉树 Marathon

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

1.二叉树的根是数组 nums 中的最大元素。
2.左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
3.右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。
返回有给定数组 nums 构建的 最大二叉树 。

示例 1：

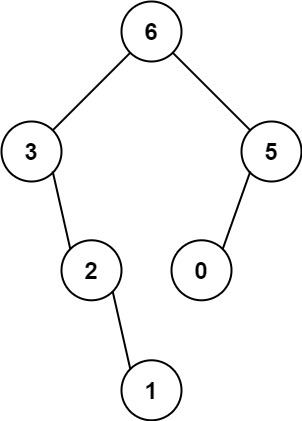
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

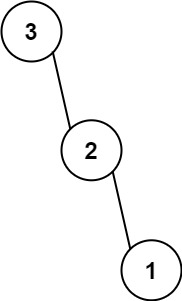
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-binary-tree

参考：

• https://leetcode-cn.com/problems/maximum-binary-tree/solution/654-zui-da-er-cha-shu-gen-ju-shu-zu-gou-q0hp9/

python

# 0654.最大二叉树
class Solution:
    def constructMaximumBinaryTree(self, nums: [int]) -> TreeNode:
        # 递归终止条件
        if not nums:
            return None
        # 最大值
        maxNum = max(nums)
        # 新建节点
        root = TreeNode(maxNum)
        # 最大点位置
        index = nums.index(maxNum)
        # 递归构建左子树
        if index > 0:
            root.left = self.constructMaximumBinaryTree(nums[:index])
        # 递归构建右子树
        if index < len(nums):
            root.right = self.constructMaximumBinaryTree(nums[index+1:])

        return root

golang

package binaryTree

import "math"

// 最大二叉树
func constructMaximumBinaryTree(nums []int) *TreeNode {
	// 递归终止条件
	if len(nums) < 1 {
		return nil
	}

	// 找最大值下标及最大值
	index := findMaxIndex(nums)
	maxNum := nums[index]

	// 构造二叉树
	root := &TreeNode{
		Val: maxNum,
		Left: constructMaximumBinaryTree(nums[:index]),
		Right: constructMaximumBinaryTree(nums[index+1:]),
	}
	return root
}

func findMaxIndex(nums []int)  int {
	maxVal := math.MinInt32
	index := 0
	for i, v := range nums {
		if v > maxVal {
			maxVal = v
			index = i
		}
	}
	return index
}