高斯-约旦消元法 理解

高斯消元是一种解方程的很巧妙的方法，核心是把方程转换成矩阵形式，然后再通过加减消元，求出值后再回带，就解出了这个方程，这里我就不赘述了。

我一般用高斯-约旦消元法，这种方法是直接转换成单位矩阵求解，减少回带次数，提高精确度，实现方式如下：

下方是一个方程

把它转换成矩阵形式就是:

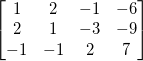
我们可以这样对其进行变换:

在第一行找到第一个元素，向下寻找有没有绝对值更大的，如果有就交换。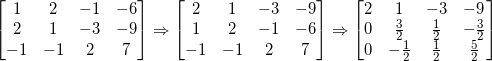

对于之后的如法炮制即可。

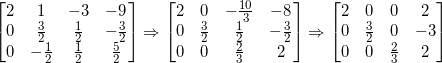
最后，我们就可以得到这样一个矩阵：很显然，在左边是单位矩阵的情况下，右边即为原方程的解。

需要注意的是，如果在转换的时候主元系数为0，这种就是无解（右边为非零数）或无穷多解（右边为零），如下为无穷多解：

可以发现，消元已经已经无法进行了。

所以，算法的思路已经出来了，接下来根据思路模拟就行了。

核心代码如下：

const double eps=1e-6;
void Guass-Jordan(){
    int r;double tmp;
    for(int i=1;i<=n;++i){
        r=i;
        for(int j=i+1;j<=n;++j)
                if(fabs(a[r][i])<fabs(a[j][i]))
                r=j;
        if(r!=i)
            swap(a[r],a[i]);
        if(fabs(a[i][i])<eps){
            p=0;
            return;
        }
        for(int j=1;j<=n;++j)
            if(j!=i){
                tmp=a[j][i]/a[i][i];
                a[j][i]=0;
                for(int k=j+1;k<=n+1;++k)
                    a[j][k]-=a[i][k]*tmp;
            }
    }
    for(int i=1;i<=n;++i)a[i][n+1]/=a[i][i];
    return;
}

恩，这就是我学了几天没学懂的东西

转载请注明地址，谢谢。