Xenia is a girl being born a noble. Due to the inflexibility and harshness of her family, Xenia has to find some ways to amuse herself.

Recently Xenia has bought nrnr red gems, ngng green gems and nbnb blue gems. Each of the gems has a weight.
Now, she is going to pick three gems.
Xenia loves colorful things, so she will pick exactly one gem of each color.
Xenia loves balance, so she will try to pick gems with little difference in weight.
Specifically, supposing the weights of the picked gems are xx, yy and zz, Xenia wants to find the minimum value of (x−y)2+(y−z)2+(z−x)2(x−y)2+(y−z)2+(z−x)2. As her dear friend, can you help her?
The first line contains a single integer tt (1≤t≤1001≤t≤100) — the number of test cases. Then tt test cases follow.
The first line of each test case contains three integers nr,ng,nbnr,ng,nb (1≤nr,ng,nb≤1051≤nr,ng,nb≤105) — the number of red gems, green gems and blue gems respectively.
The second line of each test case contains nrnr integers r1,r2,…,rnrr1,r2,…,rnr (1≤ri≤1091≤ri≤109) — riri is the weight of the ii-th red gem.
The third line of each test case contains ngng integers g1,g2,…,gngg1,g2,…,gng (1≤gi≤1091≤gi≤109) — gigi is the weight of the ii-th green gem.
The fourth line of each test case contains nbnb integers b1,b2,…,bnbb1,b2,…,bnb (1≤bi≤1091≤bi≤109) — bibi is the weight of the ii-th blue gem.
It is guaranteed that ∑nr≤105∑nr≤105, ∑ng≤105∑ng≤105, ∑nb≤105∑nb≤105 (the sum for all test cases).
For each test case, print a line contains one integer — the minimum value which Xenia wants to find.
5 2 2 3 7 8 6 3 3 1 4 1 1 1 1 1 1000000000 2 2 2 1 2 5 4 6 7 2 2 2 1 2 3 4 6 7 3 4 1 3 2 1 7 3 3 4 6
14 1999999996000000002 24 24 14
In the first test case, Xenia has the following gems:
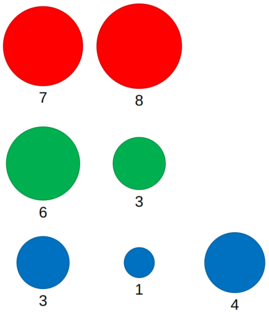
If she picks the red gem with weight 77, the green gem with weight 66, and the blue gem with weight 44, she will achieve the most balanced selection with (x−y)2+(y−z)2+(z−x)2=(7−6)2+(6−4)2+(4−7)2=14(x−y)2+(y−z)2+(z−x)2=(7−6)2+(6−4)2+(4−7)2=14.
每组都二分搜一下
#include <iostream> #include <vector> #include <algorithm> #include <string> #include <set> #include <queue> #include <map> #include <sstream> #include <cstdio> #include <cstring> #include <numeric> #include <cmath> #include <iomanip> #include <deque> #include <bitset> //#include <unordered_set> //#include <unordered_map> //#include <bits/stdc++.h> //#include <xfunctional> #define ll long long #define PII pair<int, int> #define rep(i,a,b) for(int i=a;i<=b;i++) #define dec(i,a,b) for(int i=a;i>=b;i--) #define pb push_back #define mk make_pair using namespace std; int dir[4][2] = { { 0,1 } ,{ 0,-1 },{ 1,0 },{ -1,0 } }; const long long INF = 0x7f7f7f7f7f7f7f7f; const int inf = 0x3f3f3f3f; const double pi = 3.14159265358979; const int mod = 998244353; const int N = 2e5+5; //if(x<0 || x>=r || y<0 || y>=c) inline ll read() { ll x = 0; bool f = true; char c = getchar(); while (c < '0' || c > '9') { if (c == '-') f = false; c = getchar(); } while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar(); return f ? x : -x; } ll gcd(ll m, ll n) { return n == 0 ? m : gcd(n, m%n); }void find(vector<ll> &g,vector<ll> &g1,ll x) { int pos1 = lower_bound(g.begin(), g.end(), x) - g.begin(); if(pos1<g.size()) g1.push_back(g[pos1]); if (pos1 > 0) g1.push_back(g[pos1 - 1]); } ll solve(ll nr,vector<ll> &r,vector<ll> &g, vector<ll> &b) { ll res = INF; for (int i = 0; i < nr; i++) { vector<ll> g1, b1; find(g, g1, r[i]); find(b, b1, r[i]); for (int j = 0; j < b1.size(); j++) { for (int k = 0; k < g1.size(); k++) { res = min(res, (b1[j] - g1[k])*(b1[j] - g1[k]) + (b1[j] - r[i])*(b1[j] - r[i]) + (r[i] - g1[k])*(r[i] - g1[k])); } } } return res; } int main() { int T; cin >> T; while (T--) { int nr, ng, nb; cin >> nr >> ng >> nb; vector<ll> r(nr),g(ng),b(nb); for (int i = 0; i < nr; i++) cin >> r[i]; for (int i = 0; i < ng; i++) cin >> g[i]; for (int i = 0; i < nb; i++) cin >> b[i]; ll res = INF; sort(r.begin(), r.end()); sort(g.begin(), g.end()); sort(b.begin(), b.end()); res = min(res, solve(nr, r, g, b)); res = min(res, solve(ng, g, r, b)); res = min(res, solve(nb, b, r, g)); cout << res << endl; } return 0; }
//int find(ll x,vector<ll> a)//找最近的数
//{
// int pos = lower_bound(a.begin(),a.end(),x)-a.begin();
// if (x <= a[0])
// return a[0];
// else if (x>a.back())
// return a.back();
// else
// {
// if (a[pos] - x > x - a[pos - 1])
// return a[pos - 1];
// else
// return a[pos];
// }
//}