JAVA实现通过中序遍历和后序遍历序列建树，并求树的高度，用层次遍历做验证

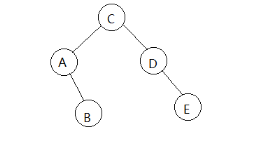
作为例子的树长这样：

package bstpractice;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class BstTest {
    public static void main(String args[]){
        
        //step1，先根据中序，后序序列建树
        List<Character> posOrder = Arrays.asList('B', 'A', 'E', 'D', 'C');
        List<Character> inOrder = Arrays.asList('A', 'B', 'C', 'D', 'E');
        System.out.println("通过");
        System.out.println("中序序列："+inOrder);
        System.out.println("后序序列："+posOrder);
        System.out.println("成功构建二叉树，其先序遍历为：");

        //建树
        MyBinarySearchTree<Character> myBST =MyBinarySearchTree.buildTree(inOrder,posOrder);
        //先序遍历
       // System.out.println("先序遍历结果：");
        System.out.println(myBST.preOrder());
        System.out.println("高度是:"+myBST.getHigh());
        System.out.println("通过其层次遍历：");
        System.out.println(myBST.levelOrder());
        System.out.println("可知正确");


    }
}

　　

package bstpractice;

import sun.reflect.generics.tree.Tree;

import java.util.*;

public class MyBinarySearchTree<E extends Comparable<? super E>> {
    public TreeNode root;
    private int size;
    private int high;

    private class TreeNode<E> {
        TreeNode left;
        TreeNode right;
        E value;

        public TreeNode(E value) {
            this.value = value;
        }
    }

    //中序、后序遍历建树方法
    public static <T extends Comparable<? super T>> MyBinarySearchTree buildTree(List<T> inOrder, List<T> posOrder) {
        MyBinarySearchTree<T> tree = new MyBinarySearchTree<>();
        tree.size = 0;
        tree.root = tree.build(inOrder, posOrder);
        return tree;
    }

    private TreeNode build(List<E> inOrder, List<E> posOrder) {
        //边界条件
        if (posOrder.isEmpty() || posOrder == null) return null;
        //if(inOrder.isEmpty()|| inOrder == null) return null;

        E e = posOrder.get(posOrder.size() - 1);//根元素
        int index = inOrder.indexOf(e);//得到划分位置和 左子树子序列长度信息，是index！！不是index-1
        TreeNode node = new TreeNode(e);
        //inOrder(0,index-1);index;(index+1,size-1)
        //posOrder(0,0+index-1);（index，size-2）;size-1;
        //subList【 ）！！！ subList【 ）！！！ subList【 ）！！！ subList【 ）！！！
        List<E> subLeftInOrder = inOrder.subList(0, index); //实际[0,index-1];
        List<E> subLeftPosOrder = posOrder.subList(0, index);
        node.left = build(subLeftInOrder, subLeftPosOrder);

        List<E> subRightInOrder = inOrder.subList(index + 1, posOrder.size());//可不是size-1 ; size 是树的大小信息...;左闭右开
        List<E> subRightPosOrder = posOrder.subList(index, posOrder.size() - 1);

        node.right = build(subRightInOrder, subRightPosOrder);
        return node;
    }


    //用栈实现层次遍历,实现方式有多种，就用上课老师讲的反式实现吧；大致思路就是用一个size记录一层的大小，集中手机层次的结点
    /*  算法：
            1.入栈根结点
            2.队列空？
                不是：
                    a.查看队列的大小，记为size；
                    b.循环控制出队列size个元素
                        1）.出结点并访问（添加到list）
                        2）.出结点有左子树？有左结点入队列
                        3）.出结点有右子树？有右节点入队列
                       返回回size个元素的Linkedlist到res中
                    c.回到2
                是:返回res列表（List）,res的元素是Linkedlist
    * */
    public List<List<E>> levelOrder(){
        List<List<E>> res = new ArrayList<>();
        if(root == null) return null;

        Queue<TreeNode> queue = new LinkedList<>(); //queue 必须用LinkedList，才有继承Queue接口
        queue.add(root);
        while(!queue.isEmpty()){
            int count = queue.size();
            List<E> oneLevelList = new ArrayList<>();
            while(count>0){
                TreeNode p = queue.remove();
                oneLevelList.add((E) p.value);
                count --;
                if(p.left!=null) queue.add(p.left);
                if(p.right!=null) queue.add(p.right);
            }
            res.add(oneLevelList);
        }
        return res;
    }


    //返回高度的方法
    public int  getHigh(){
        if(root == null) return 0;
        return high =  high(root);
    }
    private int high(TreeNode p){ //求树的高度，等于左子树和右子树高度之中较大的那个
        int leftH =0;
        int rightH =0;
       //没有子树了
       if(p.left == null && p.right == null){
           return 1;
       }

      //有左子树，递归求左子树给高度
        if(p.left !=null) {
            leftH = high(p.left)+1;
        }
      //有右子树，递归求右子树高度
        if(p.right != null){
            rightH = high(p.right)+1;
        }

        return leftH >= rightH ? leftH : rightH ;
    }

    //先实现一个递归先序遍历,NLR
    public List<E> preOrder() {
        List<E> list = new ArrayList<>();
        preOrder(root, list);
        return list;
    }

    private void preOrder(TreeNode scan, List<E> list) {

        if (scan == null) return;

        list.add((E) scan.value);
        preOrder(scan.left, list);
        preOrder(scan.right, list);

    }


}

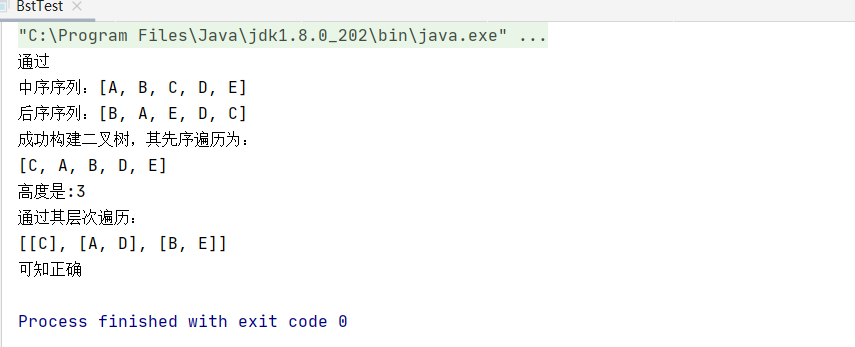
　　在IDEA中运行结果：

 注意事项：在实现建树的时候，要记得subList的参数是左闭右开的