对于机器学习和数据科学的初学者来说,必须清楚熵和交叉熵的概念。它们是构建树、降维和图像分类的关键基础。
在本文中,我将尝试从信息论的角度解释有关熵的概念,当我第一次尝试掌握这个概念时,这非常有帮助。让我们看看它是如何进行的。
什么是-log(p)?
信息论的主要关注点之一是量化编码和传输事件所需的总比特数:罕见的事件即概率较低的事件,需要表示更多位,而频繁事件不需要很多位。因此我们可以从编码器和通信机的角度出发,将-log(p)定义为编码和传输符合p概率分布的事件所需的总比特数,即信息。小 p(罕见事件)导致大 -log(p)(更多位)。
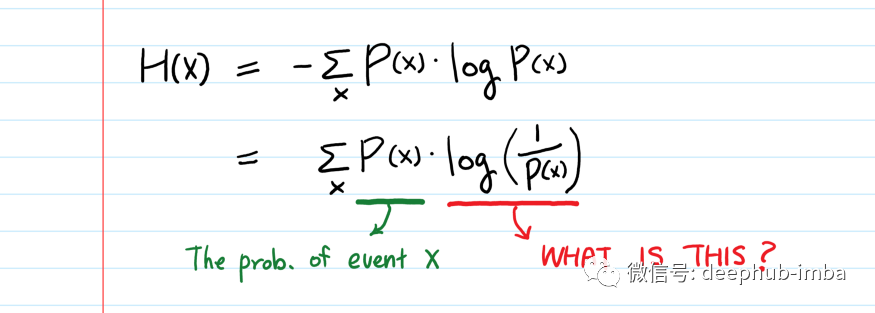
-log P(x) = log (1/P(x))
从事件观察者的角度来看,我们可以将 -log(p)理解为是观察事件的“惊讶”的程度(事件发生的概率越小,我们的惊讶程度越高)。例如如果抛硬币的 p(head) = 0.99 和 p(tail) = 0.01,如果抛硬币是tail人们肯定会惊讶。计算 -log(p(tail)) = 6.644,远大于 -log(p(head)) = 0.014。这就是 -log(p) 的直观含义。
熵,意料之中的惊喜
在上面讨论之后,我们可以定义概率分布为p(x)的事件的预期以外惊讶程度并称其为熵。正式一些的说法是:熵是量化事件可能结果中固有的不确定性水平(对我们来说不确定性带来的就是意外的惊喜,当然也有可能是惊吓)。对于连续变量 x,熵可以写为,
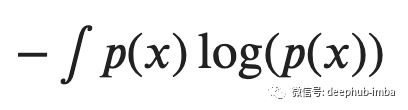
回到信息论,从编码器和通信机的角度来看,这量化了表示遵循概率分布p(x)的随机选择事件所需的比特数。例如一个包含圆形和三角形的盒子并回忆化学课上熵的概念!偏态分布(许多圆圈和少量三角形)意味着低熵,因为选择不确定性水平很低,这意味着确信选择圆圈的概率更大。
完整文章: