1.Mul（哈达玛积：对应相乘）
设：
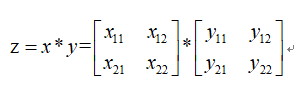
则根据偏导数的定义得：
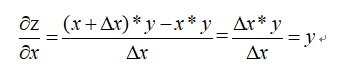
同理可得：
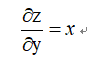
2.MatMul（矩阵乘）
矩阵乘的偏导与元素的顺序是相关的.
设：
那么：
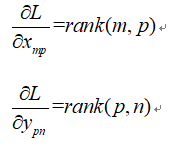
根据矩阵相容的原理：
可见矩阵的偏导数是另一个矩阵的转置，但是在用链式法则的时候需要保持和原来一直的顺序，意思是原来矩阵乘的元素在前面时，应用链式法则的时候还在前面，在后面时应用链式法则的时候，相对位置也在后面.
3.softmax
softmax with crossEntropyLoss的导数很简单，结果就是y’-y. 相比很多人都知道，网上也有很多的证明. 但是softmax的导数有时候也要单独使用，在tf源码中的tensorflow/cc/gradient/nn_grad.cc文件下，softmaxGrad函数中有段注释，意思是softmax的导数计算结果是：dL/dx = (dL/dy - sum(dL/dy * y)) * y.
其中L=f(y)，代表loss. y和x都是矩阵，维数都是[batch,class].但是文件中只有注释没有证明，在此记录下推导过程.
推导：
假设y的列数是3，其第k行元素为:
则有：
推导过softmax log-likelihood损失函数的朋友，应该很容易得到：
于是可以求出：
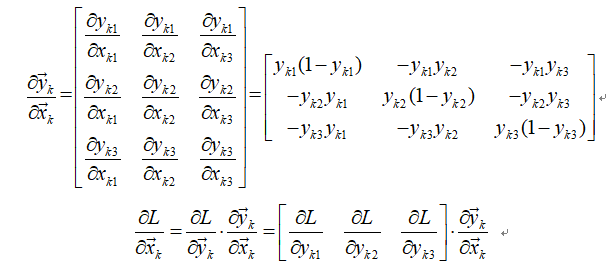
带入并化简得（以第一个元素为例）：
同理可得第二个和第三个元素为：
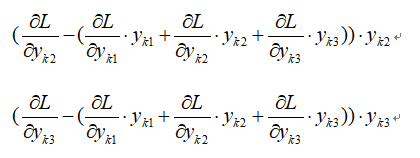
写成向量形式为：
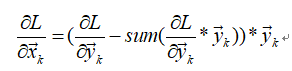
其中*代表hadmard product. 这是对每一行的求导结果. 写成矩阵形式得到：
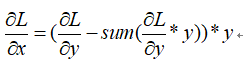
上式即是注释当中的结果.