结对编程
要求
| 软工作业 | 结对编程:实现一个自动生成小学四则运算题目的命令行程序 |
|---|---|
| 作业要求 | 结对项目要求 |
| 作业目标 | 一个自动生成小学四则运算题目的命令行程序,附带判断对错和题目查重功能 |
合作者
李纪然3218005441
陈雪莹3218005439
GitHub地址
李纪然:https://github.com/CIELIEL/3218005441
陈雪莹:https://github.com/deerc123/jiedui
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| ·Estimate | ·估计这个任务需要多少时间 | 1440 | 1680 |
| Development | 开发 | 60 | 30 |
| ·Analysis | ·需求分析(包括学习新技术) | 300 | 360 |
| ·Design Spec | ·生成设计文档 | 60 | 90 |
| ·Design Review | ·设计复审(和同事审核设计文档) | 30 | 30 |
| ·Coding Standard | ·代码规范(为目前的开发制定合适的规范) | 30 | 30 |
| ·Design | ·具体设计 | 60 | 50 |
| ·Coding | ·具体编码 | 600 | 670 |
| ·Code Review | ·代码复审 | 180 | 300 |
| · Test | ·测试(自我测试,修改代码,提交修改) | 180 | 240 |
| Reporting | 报告 | 120 | 150 |
| ·Test Report | ·测试报告 | 30 | 20 |
| ·Size Measurement | ·计算工作量 | 10 | 10 |
| ·Postmortem&Process Improvement Plan | ·事后总结,并提出过程改进计划 | 10 | 10 |
| 合计 | 1700 | 2020 |
效能分析
改进思路
改进程序耗费时间:大约8个小时
四则运算:在getresult()方法中:当碰到符号为减法时,我们通过判断左右结点的大小来决定是否调换左右结点的位置,这样就能避免生成负数的情况,当碰到符号为除法时,判断除数是否为0,为0则重新随机符号(除了/)
查重:利用DuplicateCheck类中的CompareStringByChar(String strA,String strB)方法判断两个String如果满足条件两个字符串所含元素相同、所含每个元素数量相等、字符串长度相等,就返回ture。这样可以比直接比较字符串更准确判断出题目是否相等
性能分析图
CPU占比
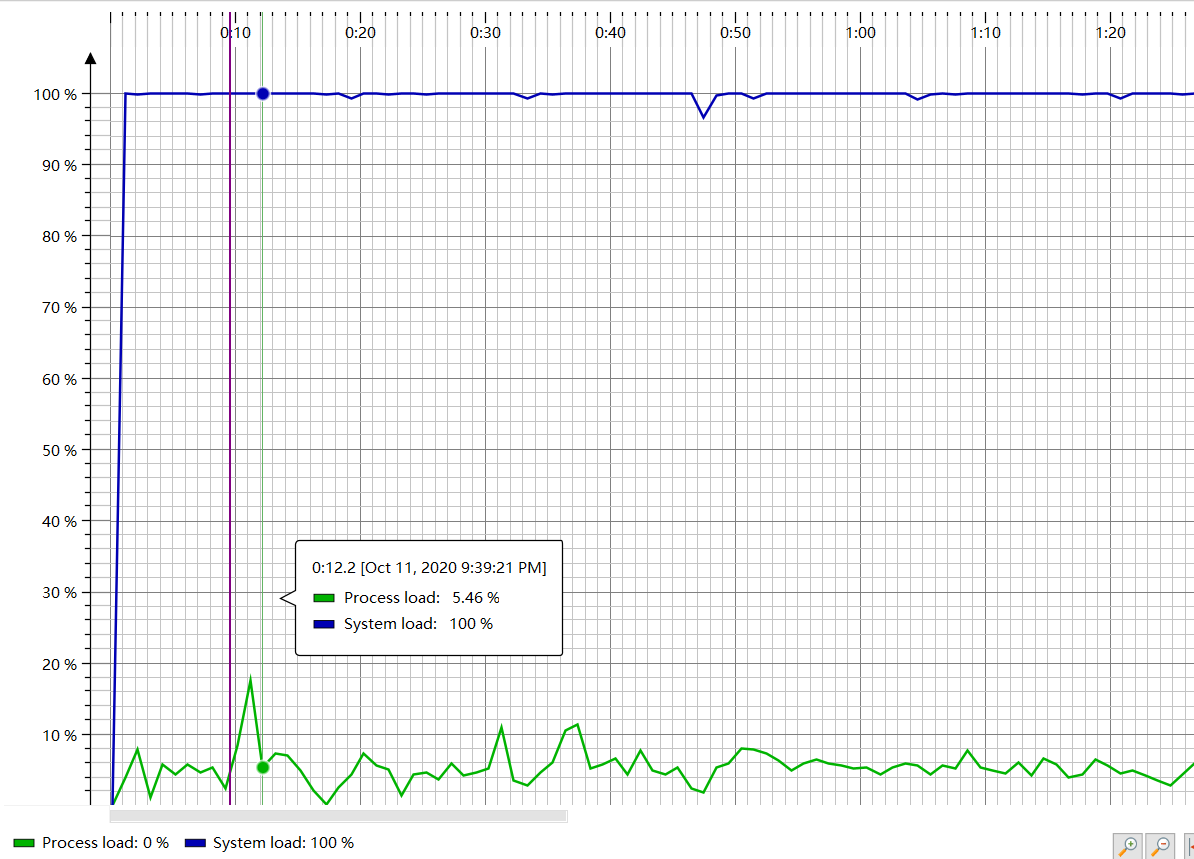
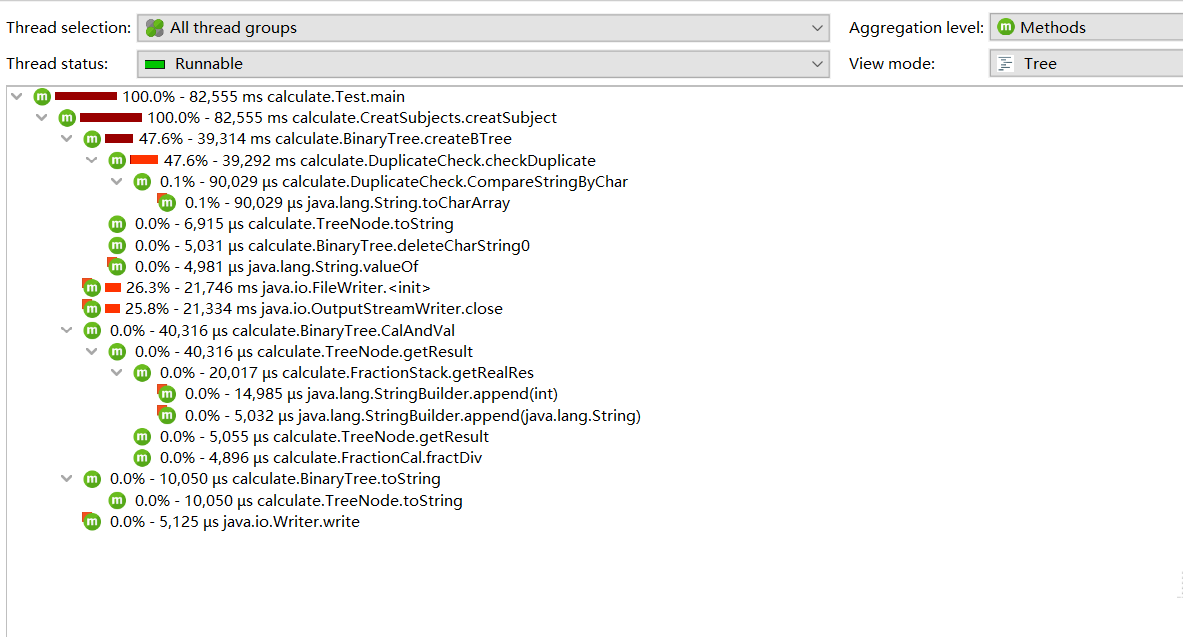
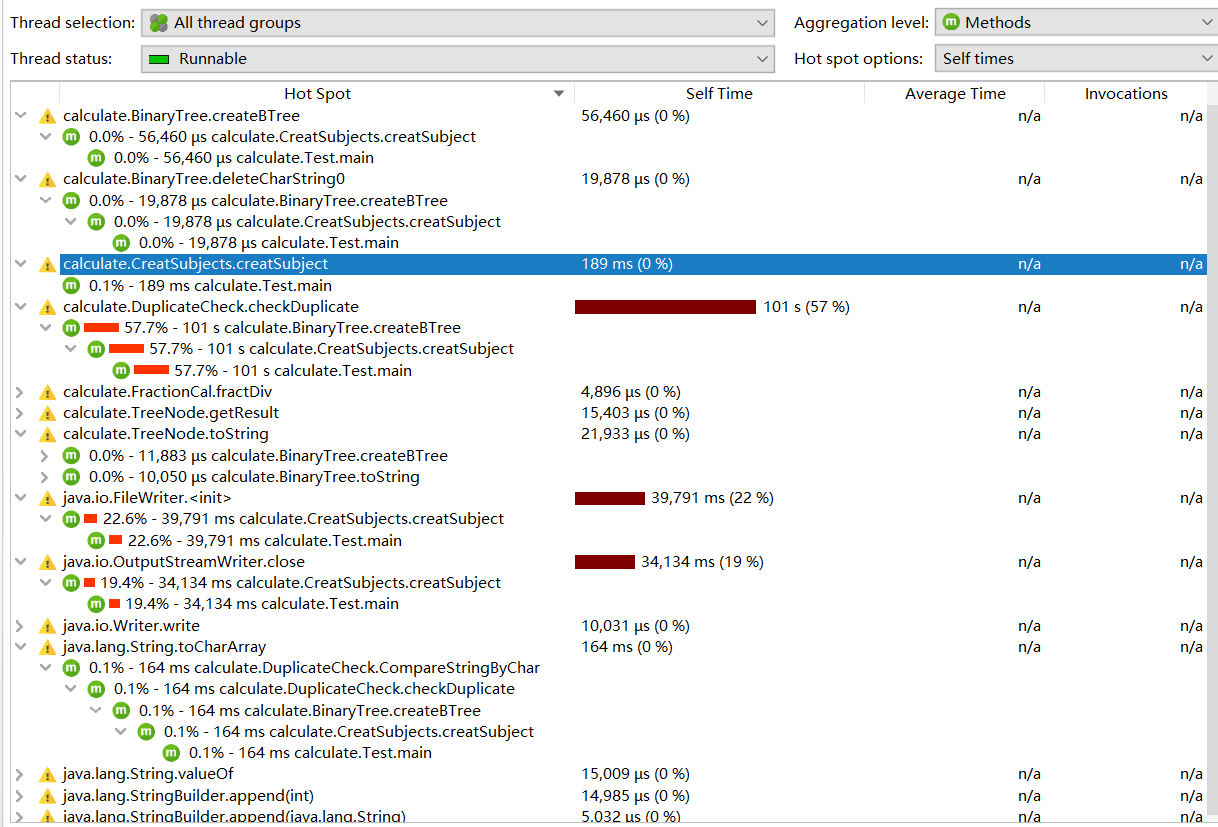
时间占比
空间占比
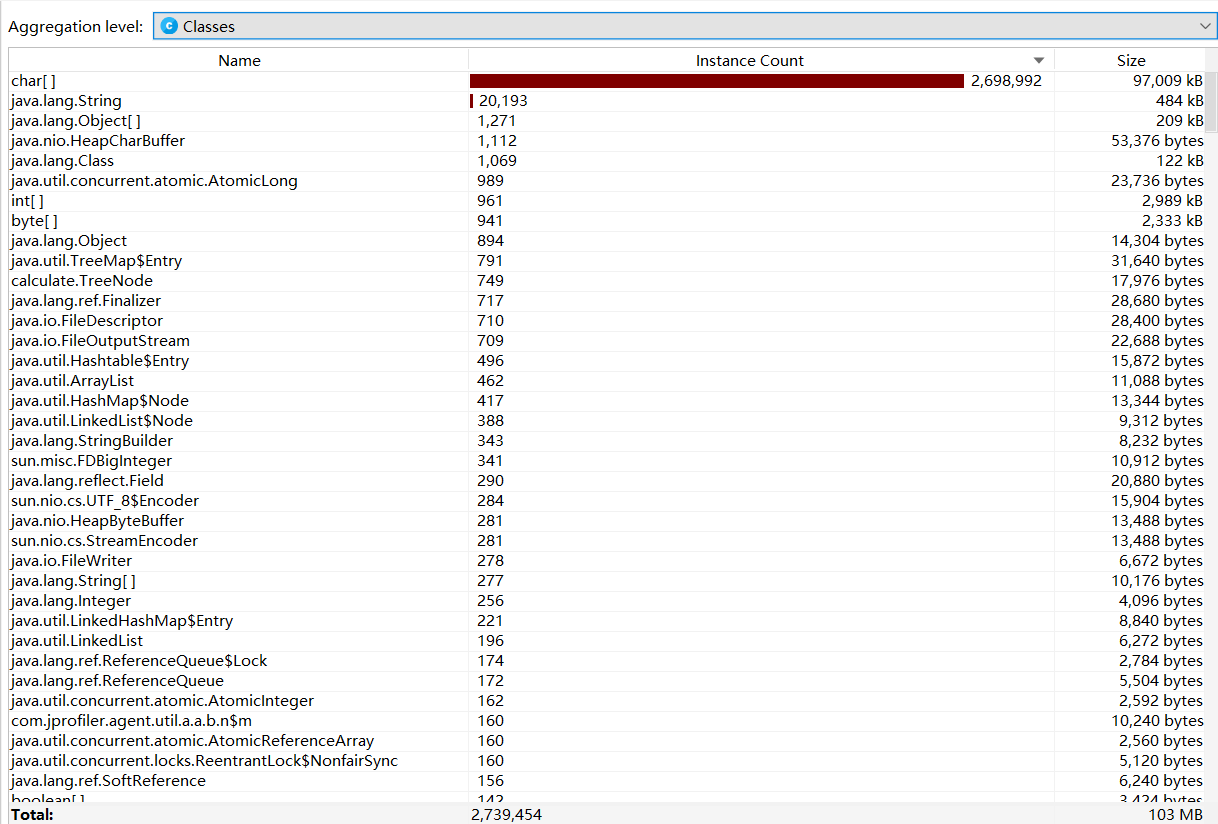
由图可得,程序中消耗最大的函数为BinaryTree类中的createBTree方法
设计实现过程
代码的类
代码关系
(Test类)主函数:输入题目数量参数和选择操作代表值—(调用)—>(CreatSubjects类)输入生成运算符数量参数,输出运行后的结果,判断答题对错
(CreatSubjects类)—(调用)—>(BinaryTree类)createBTree() 方法:生成二叉树;CalAndVal()方法:得出运行后的结果并打印到Answer文档;toString()方法:打印中序遍历二叉树的结果到Exan文档
(BinaryTree类)—(调用)—(1)(Ran类)getOperator()方法:随机生成有孩子结点的符号;getnumber()方法:获取叶子结点的数值;getChildPlace()方法:根据运算符的个数随机产生子节点的位置(2)(TreeNode类)getresult()方法:获取四则运算后的结果;toString()方法:根据去括号法则去掉多余的括号并获取去括号后的运算式
(TreeNode类)—(调用)—(1)(FractionStack类)setNumerator()方法:设置分子;setDenominator()方法:设置分母;getRealRes()方法:将分数运算后的结果转化成真分数形式(2)(FractionCal类)fracAdd()方法:进行分数加法运算;fracSub()方法:进行分数减法运算;fracMul()方法:进行分数乘法运算;fractDiv()方法:进行分数除法运算
(FractionCal类)—(调用)—(FractionStack类):分装一个分数供运算
(BinaryList类):存储二叉树以供查重
(DuplicateCheck类):查重算法
代码说明
核心代码展示
生成二叉树
public void createBTree() {
TreeNode lchild, rchild, lnode, rnode;
String check;
do {
if (num == 1) {
lchild = new TreeNode(String.valueOf(Ran.getNumber(100)), null, null);
rchild = new TreeNode(String.valueOf(Ran.getNumber(100)), null, null);
root = new TreeNode(String.valueOf(Ran.getOperator()), lchild, rchild);
} else {
int num1 = 0;
int n = getDeep() - 3;
boolean[] place = Ran.getChildPlace(num);
char rootString = Ran.getOperator();
root = new TreeNode(String.valueOf(rootString), null, null);
opeList.add(root);
//System.out.println(root.getStr());
for (int i = 0; i < n; i++) {
for (int j = 0; j < (int) Math.pow(2, i); j++, num1++) {
lchild = new TreeNode(String.valueOf(Ran.getOperator()), null, null);
rchild = new TreeNode(String.valueOf(Ran.getOperator()), null, null);
opeList.get(j + num1).setChild(lchild, rchild);
opeList.add(lchild);
opeList.add(rchild);
}
}
for (int i = 0; i < place.length; i++) {
if (place[i]) {
int a1 = Ran.getNumber(10);
lnode = new TreeNode(String.valueOf(Ran.getNumber(100)), null, null);
rnode = new TreeNode(String.valueOf(Ran.getNumber(100)), null, null);
if (i % 2 == 0) {
lchild = new TreeNode(String.valueOf(Ran.getOperator()), lnode, rnode);
opeList.add(lchild);
opeList.get(num1).setLchild(lchild);
} else {
rchild = new TreeNode(String.valueOf(Ran.getOperator()), lnode, rnode);
opeList.add(rchild);
opeList.get(num1).setRchild(rchild);
}
} else {
if (i % 2 == 0) {
lchild = new TreeNode(String.valueOf(Ran.getNumber(100)), null, null);
opeList.get(num1).setLchild(lchild);
} else {
rchild = new TreeNode(String.valueOf(Ran.getNumber(100)), null, null);
opeList.get(num1).setRchild(rchild);
}
}
num1 = num1 + i % 2;
}
//BinaryList binaryList=new BinaryList();
// String check=deleteCharString0(root.toString(),')','(');
//binaryList.saveBinary(deleteCharString0(root.toString(),')','('));
//BinaryList args=new BinaryList();
//args.args(root);
//RootSave rootSave=new RootSave();
//rootSave.saveRoot(rootString);
//binaryTreesList.add(this);
}
//check=deleteCharString0(root.toString(),')','(');
}while (DuplicateCheck.checkDuplicate(root.toString(),BinaryList.saveList)||root.getLchild()==null||root.getRchild()==null);
BinaryList.saveBinary(deleteCharString0(root.toString(),')','('));
四则运算
public String getResult(ArrayList arrayList) {
if (hasChild()) {
switch (str) {
case "+":
//左右子树如果有孩子,说明左右子树是一个表达式,而不是数字节点。
if (getRchild().hasChild() || getLchild().hasChild()) {
//判断左右邻括号的运算符是否为'/',是的话进入分数运算
if (getRchild().str.equals("/") || getLchild().str.equals("/")) {
if (getRchild().str.equals("/") && getLchild().str.equals("/")) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
return f.fracAdd(f1, f2).getRealRes();
}
if ((getLchild().str.equals("+") || getLchild().str.equals("-") || getLchild().str.equals("*") || !(getLchild().hasChild())) && getRchild().str.equals("/")) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getResult(arrayList)));
f1.setDenominator(1);
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
return f.fracAdd(f1, f2).getRealRes();
}
if (getLchild().str.equals("/") && (getRchild().str.equals("+") || getRchild().str.equals("-") || getRchild().str.equals("*") || !(getRchild().hasChild()))) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getResult(arrayList)));
f2.setDenominator(1);
FractionCal f = new FractionCal();
return f.fracAdd(f1, f2).getRealRes();
}
}
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) + Integer.parseInt(getRchild().getResult(arrayList)));
}
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) + Integer.parseInt(getRchild().getResult(arrayList)));
case "-":
//左右子树如果有孩子,说明左右子树是一个表达式,而不是数字节点。
if (getRchild().hasChild() || getLchild().hasChild()) {
//判断左右邻括号的运算符是否为'/'
if (getRchild().str.equals("/") || getLchild().str.equals("/")) {
if (getRchild().str.equals("/") && getLchild().str.equals("/")) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
if ((f.fracSub(f1, f2).getRealRes()).charAt(0) == '-') {
TreeNode treeNode = new TreeNode();
treeNode = getLchild();
this.lchild = this.rchild;
this.rchild = treeNode;
FractionCal f5 = new FractionCal();
return f5.fracSub(f2, f1).getRealRes();
}
return f.fracSub(f1, f2).getRealRes();
}
if (getLchild().str.equals("+") || getLchild().str.equals("-") || getLchild().str.equals("*") || !(getLchild().hasChild())) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getResult(arrayList)));
f1.setDenominator(1);
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
if ((f.fracSub(f1, f2).getRealRes()).charAt(0) == '-') {
TreeNode treeNode = new TreeNode();
treeNode = getLchild();
this.lchild = this.rchild;
this.rchild = treeNode;
FractionCal f5 = new FractionCal();
return f5.fracSub(f2, f1).getRealRes();
}
return f.fracSub(f1, f2).getRealRes();
}
if (getLchild().str.equals("/") && (getRchild().str.equals("+") || getRchild().str.equals("-") || getRchild().str.equals("*") || !(getRchild().hasChild()))) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getResult(arrayList)));
f2.setDenominator(1);
FractionCal f = new FractionCal();
if ((f.fracSub(f1, f2).getRealRes()).charAt(0) == '-') {
TreeNode treeNode = new TreeNode();
treeNode = getLchild();
this.lchild = this.rchild;
this.rchild = treeNode;
FractionCal f5 = new FractionCal();
return f5.fracSub(f2, f1).getRealRes();
}
return f.fracSub(f1, f2).getRealRes();
}
}
if (Integer.parseInt(getLchild().getResult(arrayList)) > Integer.parseInt(getRchild().getResult(arrayList)) || Integer.parseInt(getLchild().getResult(arrayList)) == Integer.parseInt(getRchild().getResult(arrayList))) {
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) - Integer.parseInt(getRchild().getResult(arrayList)));
}
if (Integer.parseInt(getLchild().getResult(arrayList)) < Integer.parseInt(getRchild().getResult(arrayList))) {
TreeNode treeNode = new TreeNode();
treeNode = getLchild();
this.lchild = this.rchild;
this.rchild = treeNode;
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) - Integer.parseInt(getRchild().getResult(arrayList)));
}
return this.getResult(arrayList);
}
else {
if (Integer.parseInt(getLchild().str) > Integer.parseInt(getRchild().str) || Integer.parseInt(getLchild().str) == Integer.parseInt(getRchild().str)) {
return String.valueOf(Integer.parseInt(getLchild().str) - Integer.parseInt(getRchild().str));
}
if (Integer.parseInt(getLchild().getResult(arrayList)) < Integer.parseInt(getRchild().getResult(arrayList))) {
TreeNode treeNode = new TreeNode();
treeNode = getLchild();
this.lchild = this.rchild;
this.rchild = treeNode;
return String.valueOf(Integer.parseInt(getLchild().str) - Integer.parseInt(getRchild().str));
}
// return this.getResult(arrayList);
}
case "*":
//左右子树如果有孩子,说明左右子树是一个表达式,而不是数字节点。
if (getRchild().hasChild() || getLchild().hasChild()) {
//判断左右邻括号的运算符是否为'/'
if (getRchild().str.equals("/") || getLchild().str.equals("/")) {
if (getRchild().str.equals("/") && getLchild().str.equals("/")) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
return f.fracMul(f1, f2).getRealRes();
} else if (getLchild().str.equals("+") || getLchild().str.equals("-") || getLchild().str.equals("*") || !(getLchild().hasChild())) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getResult(arrayList)));
f1.setDenominator(1);
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
return f.fracMul(f1, f2).getRealRes();
}
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getResult(arrayList)));
f2.setDenominator(1);
FractionCal f = new FractionCal();
return f.fracMul(f1, f2).getRealRes();
}
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) * Integer.parseInt(getRchild().getResult(arrayList)));
}
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) * Integer.parseInt(getRchild().getResult(arrayList)));
/**
* 获取每个节点的运算结果,并检验除法
* 1)除数为0
* 2)不能整除
* 出现以上两种情况的话将该运算符转换成其他三种运算符
*
* @return result
*/
case "/":
if (getRchild().getResult(arrayList).equals("0")||getRchild().getResult(arrayList).equals("0")) {
while (str.equals("/")) {
str = String.valueOf(Ran.getOperator());
System.out.println(str);
}
return this.getResult(arrayList);
}
//左右子树如果有孩子,说明左右子树是一个表达式,而不是数字节点。
if (getRchild().hasChild() || getLchild().hasChild()) {
//判断左右邻括号的运算符是否为'/'
if (getRchild().str.equals("/") || getLchild().str.equals("/")) {
if (getRchild().str.equals("/") && getLchild().str.equals("/")) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
return f.fractDiv(f1, f2).getRealRes();
} else if (getLchild().str.equals("+") || getLchild().str.equals("-") || getLchild().str.equals("*") || !(getLchild().hasChild())) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getResult(arrayList)));
f1.setDenominator(1);
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getLchild().getResult(arrayList)));
f2.setDenominator(Integer.parseInt(getRchild().getRchild().getResult(arrayList)));
FractionCal f = new FractionCal();
return f.fractDiv(f1, f2).getRealRes();
}
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getLchild().getRchild().getResult(arrayList)));
FractionStack f2 = new FractionStack();
f2.setNumerator(Integer.parseInt(getRchild().getResult(arrayList)));
f2.setDenominator(1);
FractionCal f = new FractionCal();
return f.fractDiv(f1, f2).getRealRes();
}
else if (Integer.parseInt(getLchild().getResult(arrayList)) % Integer.parseInt(getRchild().getResult(arrayList)) != 0) {
if (arrayList.indexOf(this) == 0) {
FractionStack f1 = new FractionStack();
f1.setNumerator(Integer.parseInt(getLchild().getResult(arrayList)));
f1.setDenominator(Integer.parseInt(getRchild().getResult(arrayList)));
return f1.getRealRes();
}
}
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) / Integer.parseInt(getRchild().getResult(arrayList)));
}
/* while (str.equals("/")) {
str = String.valueOf(Ran.getOperator());
}*/
//return this.getResult(arrayList);
return String.valueOf(Integer.parseInt(getLchild().getResult(arrayList)) / Integer.parseInt(getRchild().getResult(arrayList)));
}
}
return str;
}
查重算法
public class DuplicateCheck {
private ArrayList<TreeNode> sameRootList = new ArrayList<>();
// public boolean duplicateCheck(Character root, BinaryTree binaryTree) {
// return true;
// }
public static boolean CompareStringByChar(String strA,String strB)
{
boolean IsEqual = true;
char[] arrA = strA.toCharArray();
char[] arrB = strB.toCharArray();
for (int i=0;i<arrA.length;i++)
{
char c=arrA[i];
if (strB.indexOf(c)==-1)
{
IsEqual = false;
}
else
{
if(GetSameCharCount(c,arrA)!=GetSameCharCount(c,arrB))
{
IsEqual = false;
}
}
}
for(int k=0;k<arrB.length;k++)//char charb in arrB
{
char b=arrB[k];
if (strA.indexOf(b)==-1)//!strA.Contains(charb)
{
IsEqual = false;
}
else
{
if (GetSameCharCount(b, arrA) != GetSameCharCount(b, arrB))
{
IsEqual = false;
}
}
}
return IsEqual;
}
//获得某字符在字符串中的数量
private static int GetSameCharCount(Character chara,char[] arrChar)
{
int count = 0;
for(int j=0;j<arrChar.length;j++)
{
if(chara.equals(arrChar[j]))
{
count++;
}
}
return count;
}
public static boolean checkDuplicate(String strA,ArrayList arrayList){
int co=0;
for(int q=0;q<arrayList.size();q++){
if (CompareStringByChar(strA,(String) arrayList.get(0))){
co++;
}
}
return co!=0;
}
}
思路

对于这样一棵二叉树,每个叶子节点都是数字,每个父节点都是符号,然后中序遍历结果就是我们所需要的四则运算,而且每次父节点返回的时候,可以根据符号进行运算式的计算,中序遍历的结果:
*1+2-3*4*
但是如何产生括号呢?
有一个简单的办法就是父节点每次返回的时候带上括号,于是运算式就变成了这样:
*((1+2)-(3*4))*
正确的优先级应该是这样的:*'('、')'>'*'、'/'>'+'、'-'*
通过整理,我们可以得到这样的规律:
假设待去括号的表达式为 (m1 op1 n1) op (m2 op2 n2) 这里m1、n1、m2、m2可能自身就是个表达式,也可能是数字,op、op1、op2为运算符
*1、若op为'/',则 (m2 op2 n2)的括号必须保留;*
*2、若op为'*'或'-',如果op2为'+'或'-',则(m2 op2 n2)的括号必须保留;*
*3、若op为'*'或'/',如果op1为'+'或'-',则(m1 op1 n1)的括号必须保留;*
*4、 除此之外,去掉括号不影响表达式的计算顺序。*
至此,我们就能得到一个比较随机的四则运算式。
测试运行
代码测试
生成10到题目(输入操作参数1)

生成Exam文档
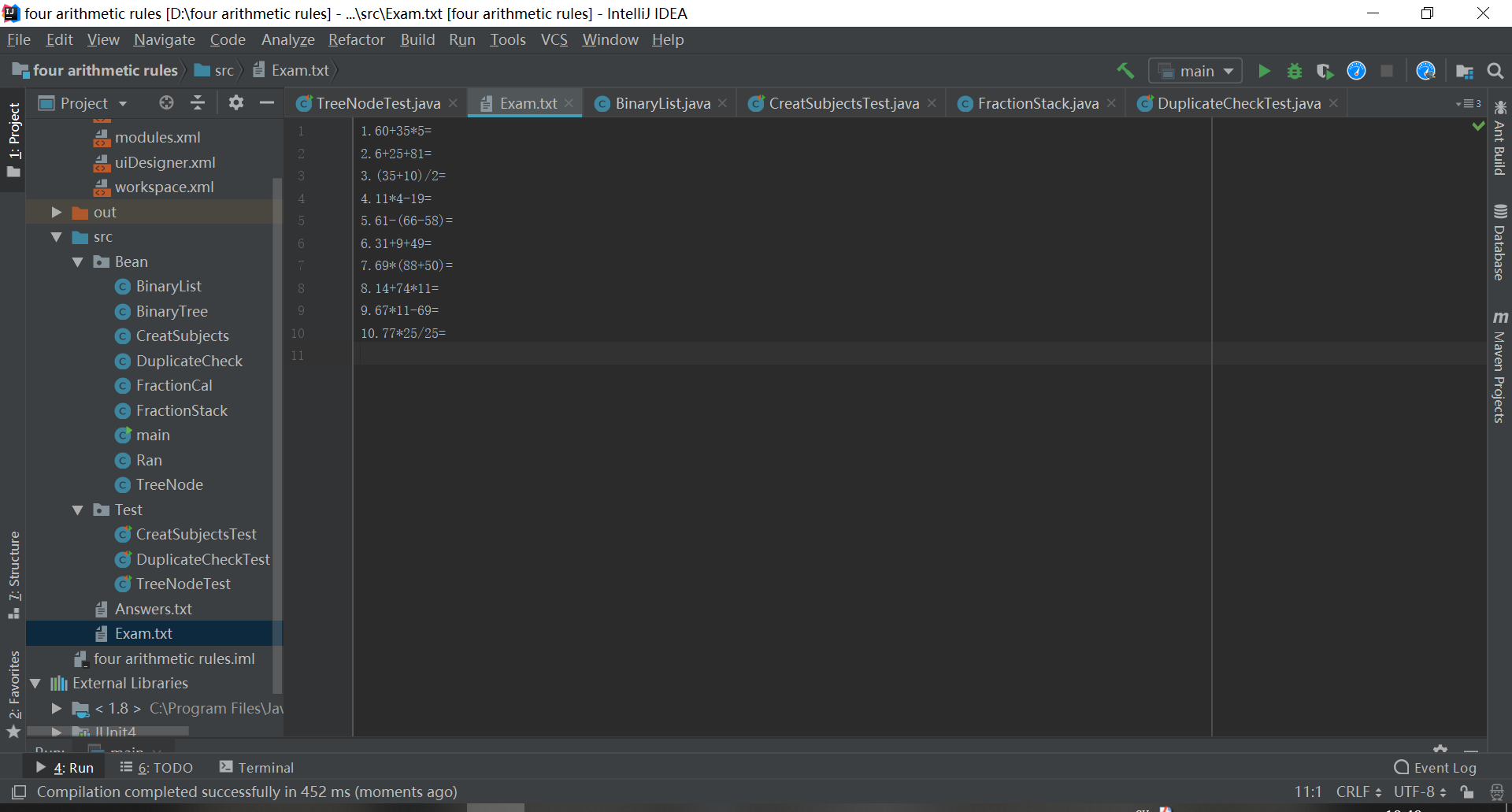
生成Answer文档

在Exam里答题后(输入操作参数2)

答题
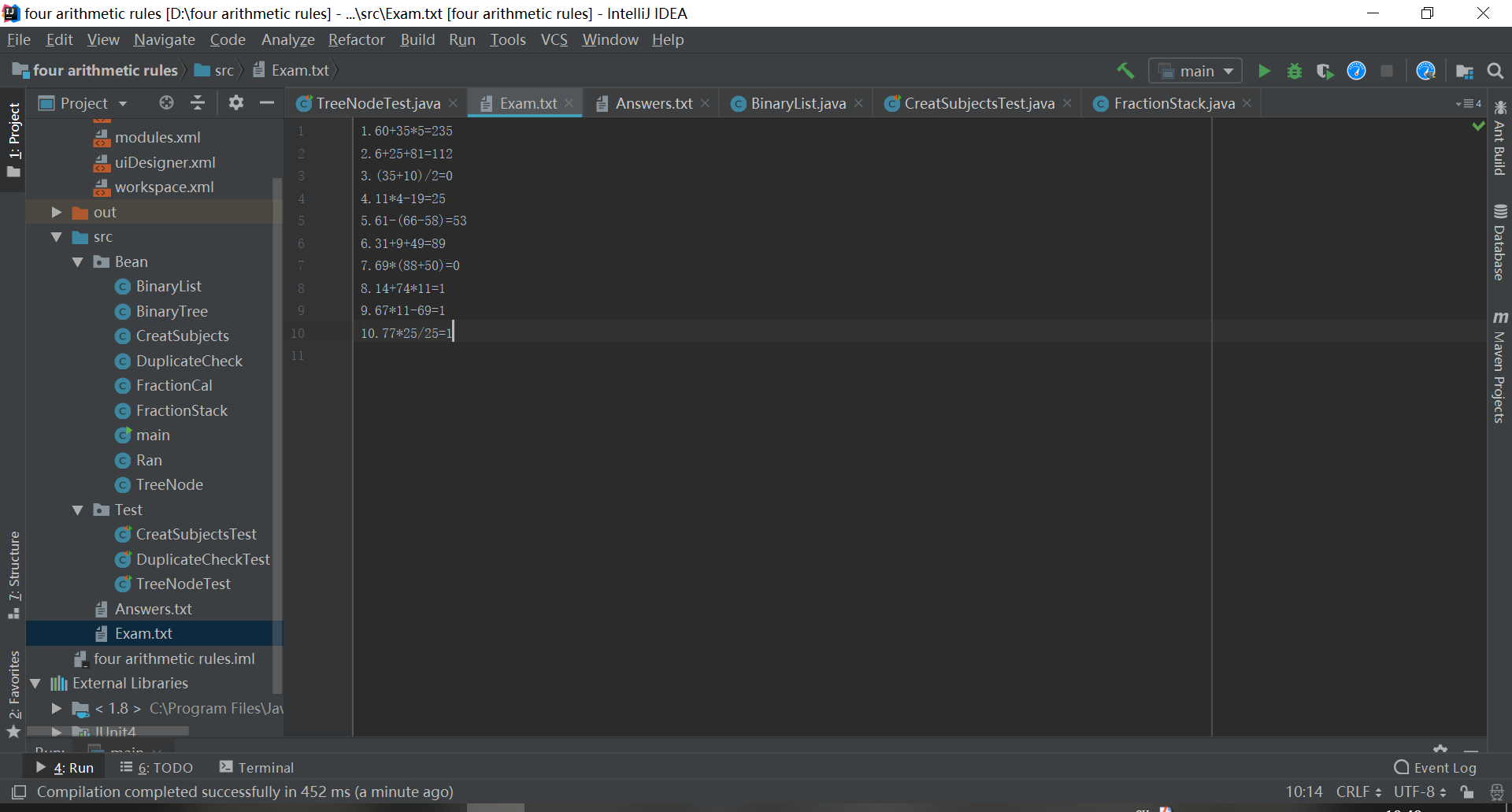
批改后
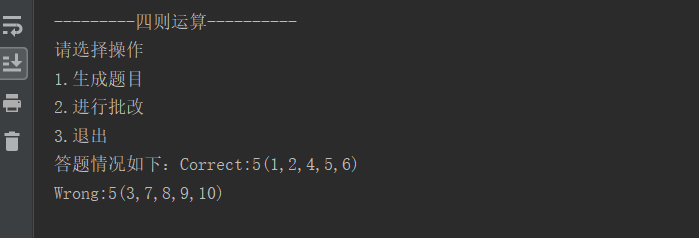
单元测试
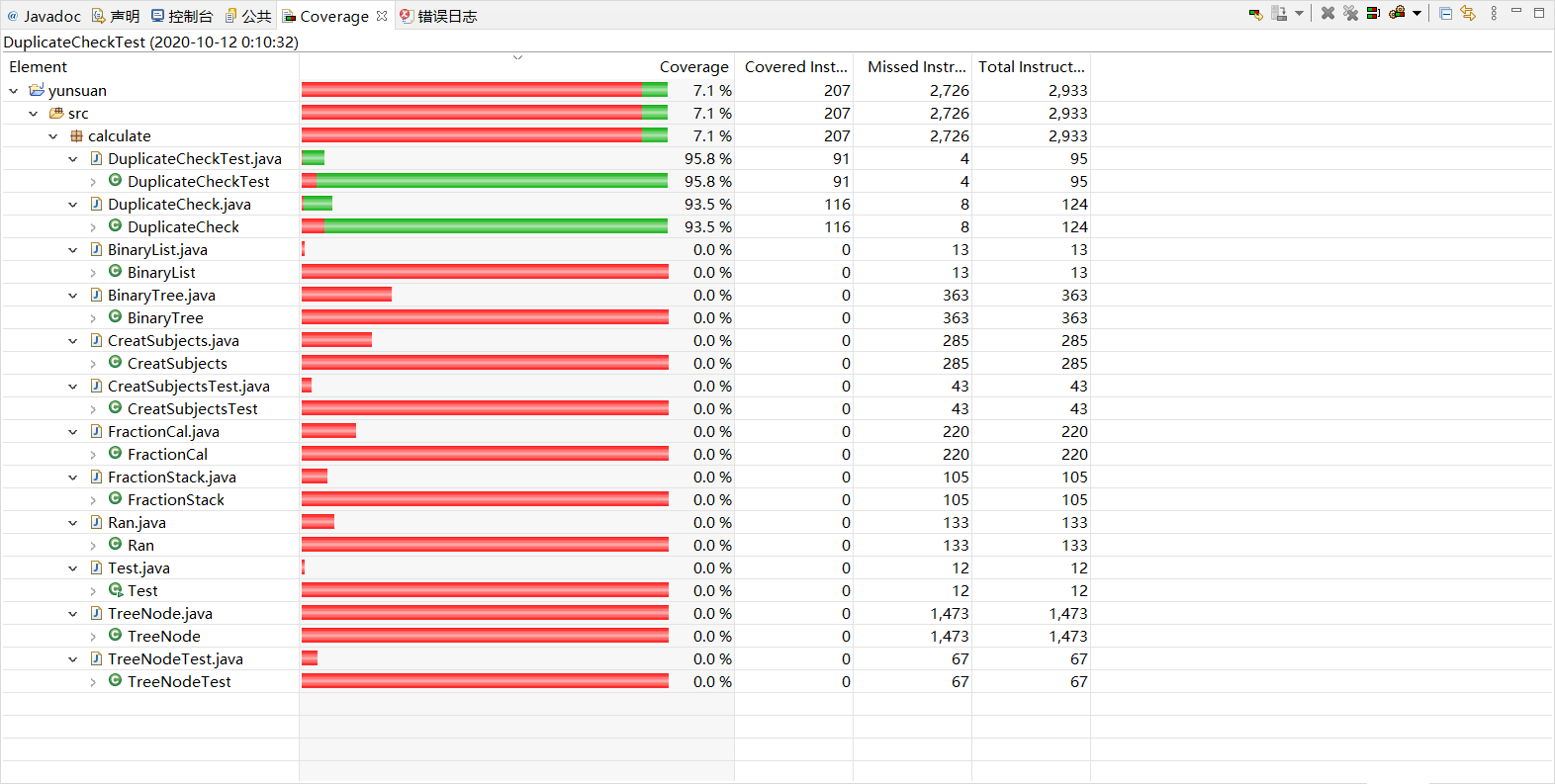
分别对creatSubjects类、TreeNode类、DuplicateCheckTest类进行了单元测试,运行成功截图以及代码覆盖率截图如下
creatSubjects类
我们分别测试了生成10000道题目、100道题目,测试均成功。

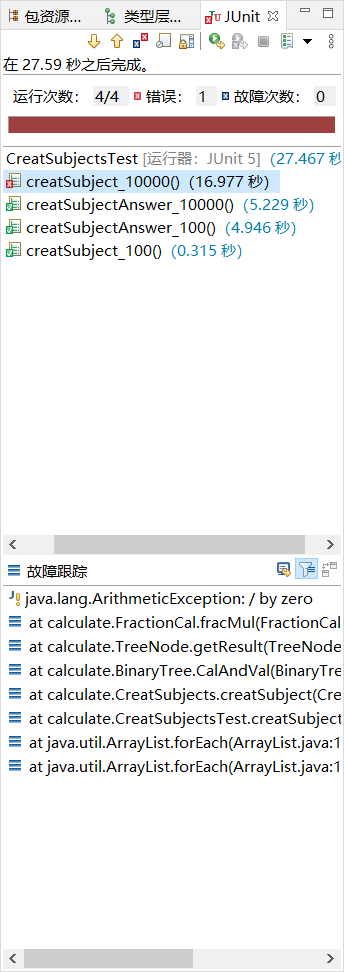
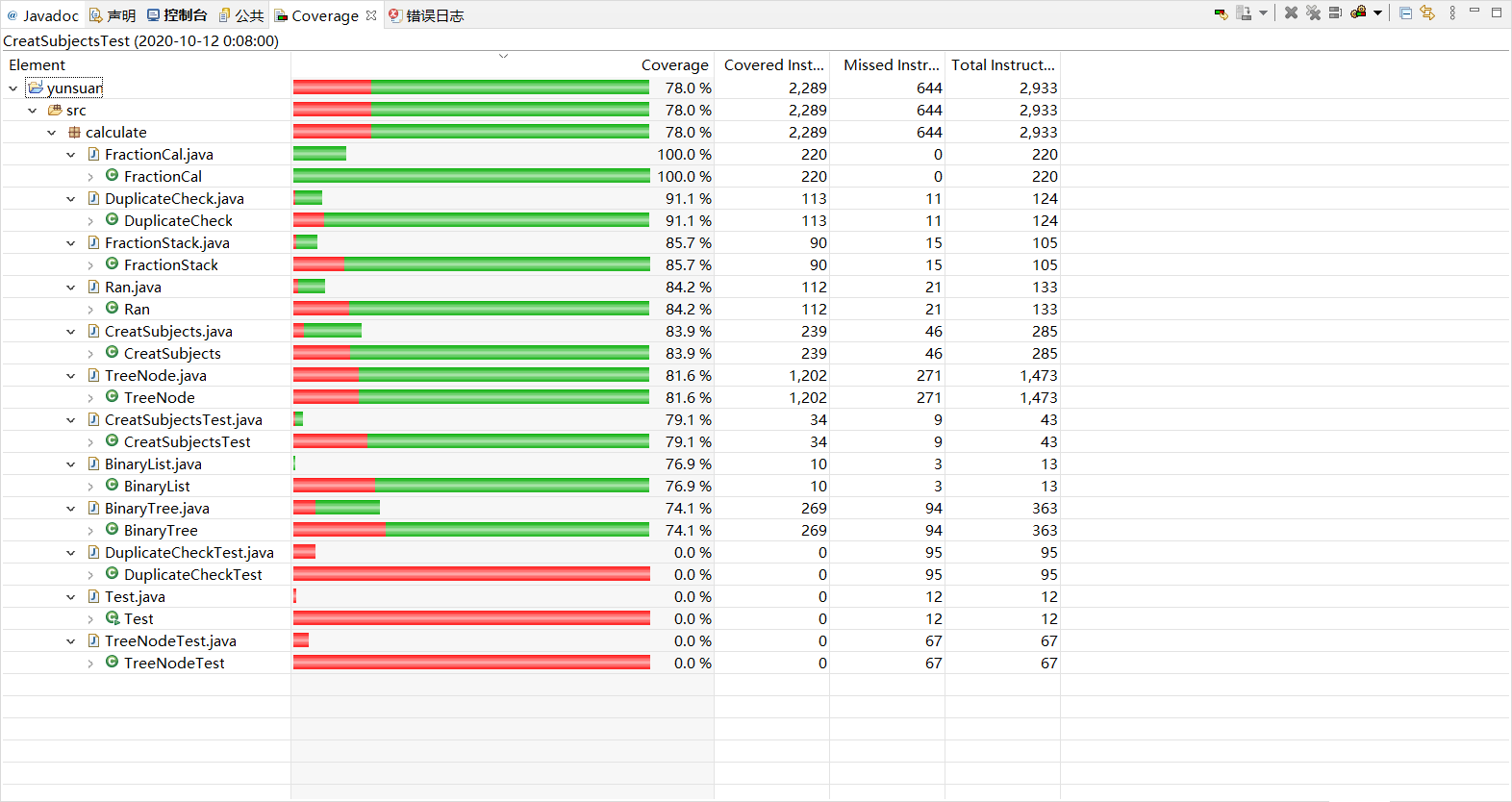
TreeNode类

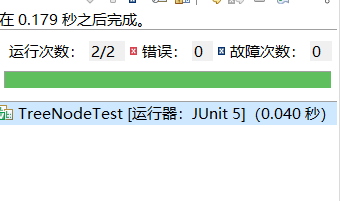
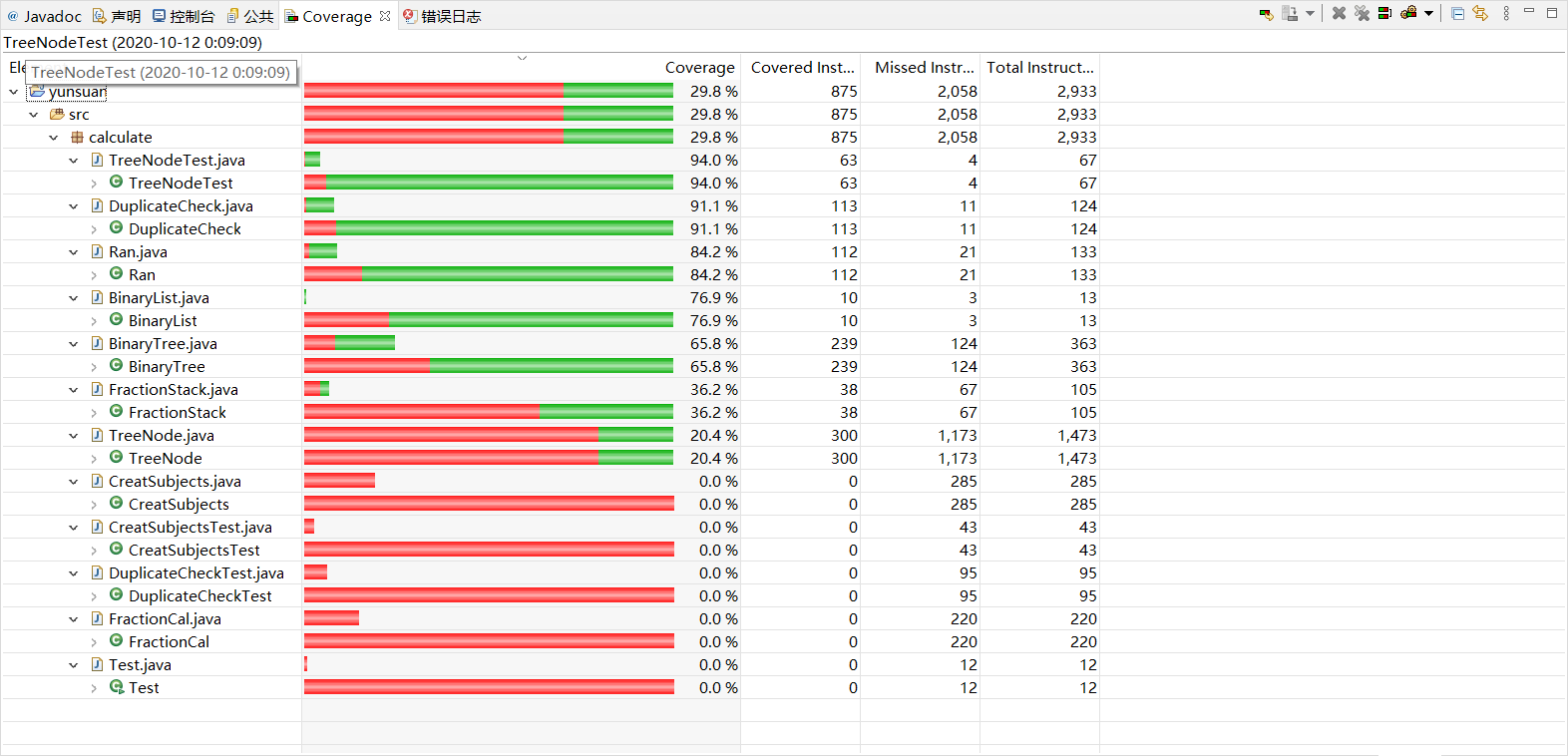
DuplicateCheckTest类
项目小结
李纪然项目小结
我发现写代码要理清思路,逻辑清晰,才能更好的用代码实现自己的思路
陈雪莹项目小结
这次结对项目让我深有感触,两个人的合作果然是比一个人单干要效率高!