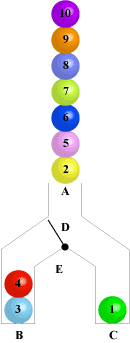
有一个筒,从A口可以放球,放进去的球可通过挡板DE使其掉进B管或C管里,现有带1-10标号的球按给定顺序从A口放入,问是否有一种控制挡板的策略可以使B管和C管中的球从下往上标号递增。
输入:
第一行输入数据组数N。接下来N行为N组具体数据,每组数据中有10个整数,代表球的放入顺序。
输出:
对于每组数据,若策略存在,输出YES;若不存在,输出NO
解法1:DFS
思路:每次判断当前小球是否大于左边容器的最上端的小球,如果可以就放,否则再去看右边的。一旦发现左右两边都不能放,那就只能判定是NO了。
#include<cstdio>
#include<string>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int INF = 0x7FFFFFFF;
const int maxn = 1e5 + 10;
int a[11],vis[11],flag;
void dfs(int x,int l,int r)
{
int i;
if(x==11)return;
if(flag)return;
if(a[x]>l)dfs(x+1,a[x],r);
else if(a[x]>r)dfs(x+1,l,a[x]);
else{flag=1;return;}
}
int main()
{
int T,i,j,k;
scanf("%d",&T);
while(T--)
{
flag=0;
for(i=1;i<=10;i++)
scanf("%d",&a[i]);
memset(vis,0,sizeof(vis));
dfs(1,0,0);
if(flag)printf("NO
");
else printf("YES
");
}
return 0;
}
解法2:二进制枚举
思路:看作0,1序列
#include<cstdio>
#include<cstring>
int a[15], l[15], r[15], t, i, j, lc, rc, cnt;
bool vis[15], flag;
bool solve()
{
for (i = 0; i < 1024; ++i)
{
memset(l, 0, sizeof(l));
memset(r, 0, sizeof(r));
lc = rc = 0;
for (cnt = 0, j = i; cnt < 10; ++cnt, j >>= 1)
{
if (j & 1) l[lc++] = a[cnt];
else r[rc++] = a[cnt];
}
flag = true;
for (j = 1; j < lc; ++j)
if (l[j] < l[j - 1])
{
flag = false;
break;
}
if (flag)
for (j = 1; j < rc; ++j)
if (r[j - 1] > r[j])
{
flag = false;
break;
}
if (flag) return true;
}
return false;
}
int main()
{
scanf("%d", &t);
while (t--)
{
memset(vis, 0, sizeof(vis));
for (i = 0; i < 10; ++i)
scanf("%d", &a[i]);
puts(solve() ? "YES" : "NO");
}
return 0;
}
bitset增强版
#include <iostream>
#include <bitset>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin >> n;
while (n--)
{
int ball[10];
for (int i = 0; i < 10; ++i)
{
cin >> ball[i];
}
bitset<10> direction;
int all = 1024;
while (all-- > 0)
{
direction = static_cast<bitset<10> >(all);
bool perfect = true;
int left = 0;
int right = 0;
for (int i = 0; i < 10; ++i)
{
if (direction[i])
{
if (ball[i] > left)
{
left = ball[i];
}
else
{
perfect = false;
break;
}
}
else
{
if (ball[i] > right)
{
right = ball[i];
}
else
{
perfect = false;
break;
}
}
}
if (perfect)
{
break;
}
}
if (all >= 0)
{
cout << "YES" << endl;
}
else
{
cout << "NO" << endl;
}
}
return 0;
}