HDU 1384 Intervals【差分约束-SPFA】

类型：给出一些形如a−b<=k的不等式（或a−b>=k或a−b<k或a−b>k等），问是否有解【是否有负环】或求差的极值【最短/长路径】。
例子：b−a<=k1，c−b<=k2，c−a<=k3。将a，b，c转换为节点；k1，k2，k3转换为边权；减数指向被减数，形成一个有向图：

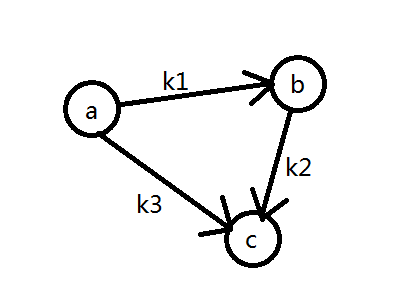
由题可得（b−a） + （c−b） <= k1+k2，c−a<=k1+k2。比较k1+k2与k3，其中较小者就是c−a的最大值。
由此我们可以得知求差的最大值，即上限被约束，此时我们拿最小的限制，也就是跑最短路；反之，求差的最小值，下限被约束，我们跑最长路。
跑最短路时：d[v]<=d[u]+w
跑最长路时：d[v]>=d[u]+w
路径中可能会存在负边，用SPFA跑。判断负环，最短最长路均可

题意：

[a,b]区间内有>=c个数，计算集合里至少多个元素

思路：

因为数据范围 0 <= ai <= bi <= 50000，可以设s[i]为i之前元素个数【不含i】,将题意转化为差分约束，s[b+1]-s[a]>=c，防止a-1出界。

求s[end]>=?，求下限，求最长路，注意数组初始化和d数组更新条件

解决不连通有两个方法：

1. 新增特殊点或在区间内以1为单位连通

2.所有点全部入队，并标记

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int N=50005;
int n,cnt;
const int INF=0x3f3f3f3f;
int head[N],d[N];
bool vis[N];

struct e{
    int to,next,w;
}edge[N<<2]; // 有反向边

void add(int u,int v,int w){
    edge[cnt].w=w;edge[cnt].to=v;edge[cnt].next=head[u];head[u]=cnt++;
}

void init(){
    cnt=0;
    memset(head,-1,sizeof(head));
}

void SPFA(int s)
{
    memset(d,-INF,sizeof(d));
    memset(vis,0, sizeof(vis));
    queue<int> q;
    q.push(s);
    d[s]=0;
    vis[s]=1;
    while(q.size())
    {
        int u = q.front();q.pop();
        vis[u]=0;
        for(int i=head[u];i!=-1;i=edge[i].next)
        {
            int v=edge[i].to;
            int w=edge[i].w;
            if(d[v]<d[u]+w)
            {
                d[v]=d[u]+w;
                if(!vis[v])
                {
                    q.push(v);
                    vis[v]=1;
                }
            }
        }
    }
}


int main(){
    while(scanf("%d",&n)!=EOF) {
        init();
        int st = INF, ed = -INF;
        for (int i = 1; i <= n; i++) {
            int a, b, c;
            cin >> a >> b >> c;
            add(a, b + 1, c);
            st = min(st, a);
            ed = max(ed, b + 1);
        }
        for (int i = st; i < ed; i++) {
            add(i, i + 1, 0);
            add(i + 1, i, -1);
        }
        SPFA(st);
        cout << d[ed] << endl;
    }
    return 0;
}