一阶导数与二阶导数的计算
图像(I)可以看作((x, y) in N^2 o N)的映射: (i = f(x, y)). 其中(N)为正整数.很明显(f)在定义域上是不连续的.
不连续函数(f(x, y))的导数, 严格来说不算能算作导数, 只是形式上与真正的导数相似. 取(Delta x = 1), 一阶与二阶偏导数分别为:
[frac {partial f}{partial x} = f(x + 1) - f(x)
]
or
[frac {partial f}{partial x} = f(x) - f(x -1)
]
[frac {partial^2 f}{partial x^2} = frac {partial f'}{partial x} = f'(x + 1) - f'(x) = f(x + 1) - f(x) - f(x) - f(x-1) = f(x + 1) + f(x -1) - 2f(x)
]
为简单起见, (f(x, y))简写成(f(x)), 因为求关于(x)的偏导数时(y)是恒定的.
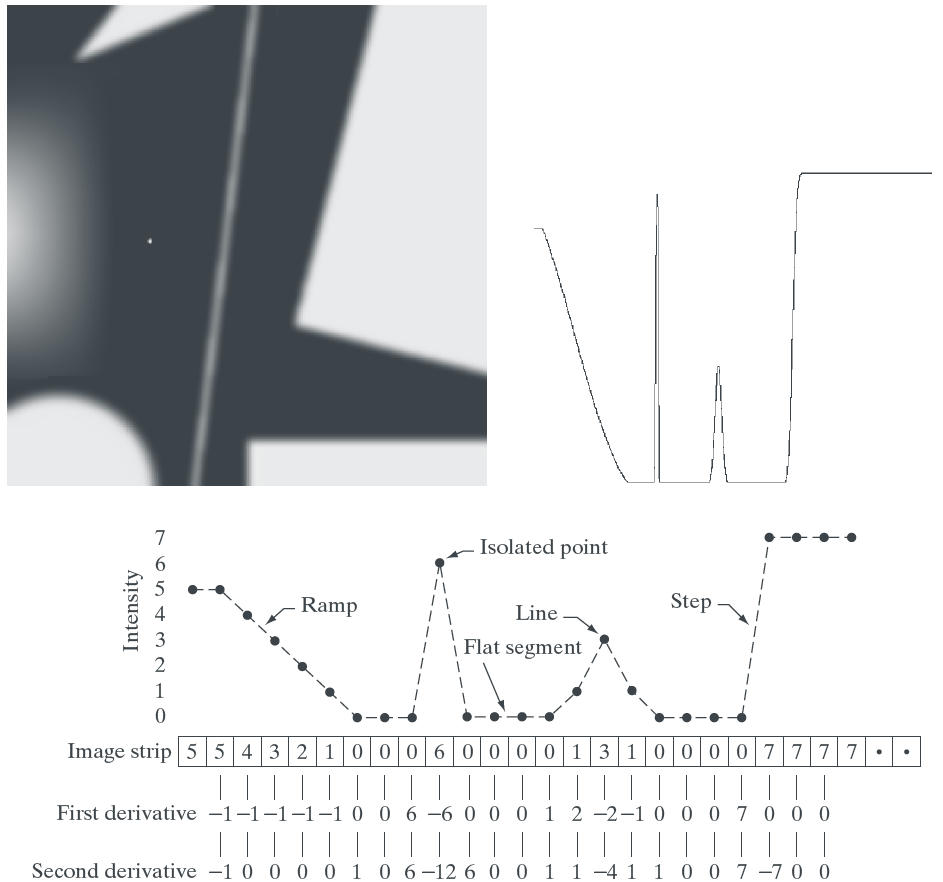
作为Spatial Domain Filter的特点
- 一阶导数提取出来的边缘较粗,
- 二阶导数对细节更敏感, 如细线, 噪声等. 它提取出来的边缘更细更强(sharp)
- 二阶导数的符号可用来判断一个转变(transition)是从亮到暗或者相反.
- 应用二阶导数时容易出现double-line effect. (中间位置的二阶导数值与两边的往往不同). 出现双线效应的前提是线本身的宽度小于mask, 否则就不当作线, 而是region了.(见10.2.3)
注意, 上面的中间和两边的含义是: 只在一条水平线考察图片, (x)处理edge上为中间位置, (x-1, x+1)为两边位置.

# Reference * Digital Image Processing, 3rd edition, Chapter 10