intensity梯度值分布跟图片的大小有关, 比如将一张小图片放大后会变得很模糊, 原先清晰的edge, 即大的梯度值变得模糊. 但是原有的边缘通常还是肉眼可分辨的. 但用Sobel 算子可能就检测不出来的. 为了应付不同scale与blur程度图片的边缘检测, 检测算子需要能大能小, 大的用于检测大而blur的图片上的边缘, 小的用于检测精细的边缘. Sobel算子无法满足这个要求.
其实到现在已经可以看出对边缘检测算子的两个要求:
- 可以计算一阶或二阶导数
- 可大可小
Laplacian of Gaussian(LoG)就满足这样的要求.
LoG的定义
LoG里的Gaussian是期望为0的二元正态分布:
[G(x, y) = e^{- frac {x^2 + y^2}{2sigma^2}}
]
它的Laplacian算子为:
[ riangledown^2 G = frac {partial^2 G}{partial x^2} + frac {partial^2 G}{partial y^2} = left[ frac {x^2 + y^2 - sigma ^ 4}{sigma ^ 2}
ight] e ^{-frac{x^2 + y^2}{2sigma^2}}
]
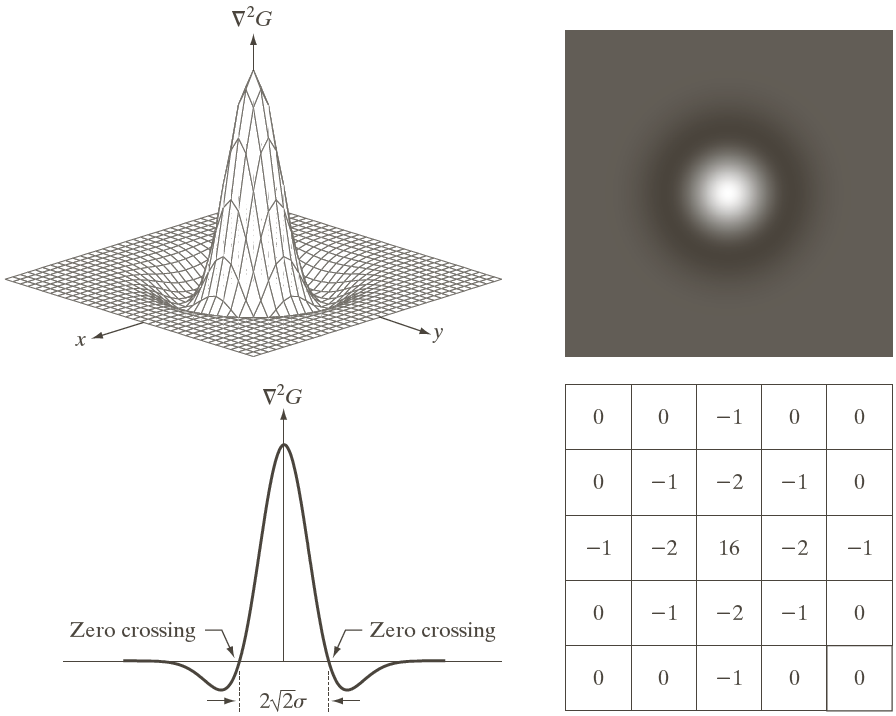
指定mask大小以后, 通过采样可以得到近似的mask. 采样的方法不是唯一的, 唯一的要求是保留( riangledown^2 G)的函数形态.
得到mask之后进行conv操作.
整个变换可以表示为:
[T(x, y) = riangledown^2 G(x, y) odot I(x, y) = riangledown^2 [G(x, y) odot I(x, y))]
]
其中, $ odot(代表conv操作. 可以交换计算顺序的原因是)Laplacian$也是一个线性操作(通过mask实现), conv操作也是.
Marr-Hildreth edge detection算法
算法步骤:
- 高斯平滑
- 计算Laplacian
- 寻找zero-crossing点(相反方向的两个相邻点的符号相反的点, 原理见前文的第二张图), 作为edge上的点