题目来源:http://poj.org/problem?id=1031
题目大意:
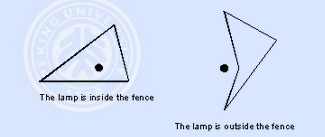
有一个光源位于(0,0)处,一个多边形的围墙。围墙是“全黑”的,不透光也不反射光。距光源r处的光强度为I0=k/r,k为常数。
一块无穷窄高为h的墙上围墙受到的照度为dI=I0*|cosα|*dl*h,其中I0为该点光强,α为法线与该点到光源连线的夹角。
求总照度。(dI之和)
输入:第一行三个数,第一个数为给定的常数k,第二个数位围墙高h,第三个数为围墙顶点数。接下来每行为一个围墙的顶点,按遍历多边形的顺序给出。
输出:总的照度。
Sample Input
0.5 1.7 3 1.0 3.0 2.0 -1.0 -4.0 -1.0
Sample Output
5.34
如果有一点点计算机视觉的基础或者物理直觉好的话,会知道结果实际与距离和夹角都没有关系,只要求光源向360°辐射的范围内,有多大的角度被墙挡住了。于是转化为了求围墙相对于光源张角的问题。
求张角的过程大致如下:
遍历所有的边,求边相对于光源的张角(自行规定一个正方向)。记录下每次求和之后的最大值和最小值(即像一个方向延扫得最远时的角度),但要注意不应该大于360度。

1 ////////////////////////////////////////////////////////////////////////// 2 // POJ1031 Fence 3 // Memory: 280K Time: 47MS 4 // Language: C++ Result: Accepted 5 ////////////////////////////////////////////////////////////////////////// 6 7 #include <iostream> 8 #include <math.h> 9 10 #define M_PI 3.14159265 11 12 using namespace std; 13 14 double k,h,x[101],y[101]; 15 double angle(double x0, double y0, double x1, double y1) { 16 double a=atan2(y0, x0); 17 double b=atan2(y1, x1); 18 if (b - a > M_PI) a += 2 * M_PI; 19 if (a - b > M_PI) b += 2 * M_PI; 20 return a-b; 21 } 22 23 int main () { 24 int i,n; 25 cin >> k >> h >> n; 26 for (i=0; i<n; i++) { 27 cin >> x[i] >> y[i]; 28 } 29 x[n] = x[0], y[n] = y[0]; 30 31 double min = 0, max = 0, sum = 0; 32 33 for(i = 0; i < n; i++) { 34 double temp = angle(x[i], y[i], x[i + 1], y[i + 1]); 35 sum += temp; 36 if (sum < min) min = sum; 37 if (sum > max) max = sum; 38 if (max - min >= 2 * M_PI) { 39 max = min + 2 * M_PI; 40 break; 41 } 42 } 43 printf("%.2lf ", k * h * (max - min)); 44 system("pause"); 45 return 0; 46 }
