1. 前言:
这次笔试是少数几次我自己独立完成的,但是结果并不好写了两道题目。起初我们实验室三个人,商量着一人做一道,因为两个小时做4道题目,对我们这些菜鸡来说几乎是不可能完成的任务。但结果是,都tmd快考完了,我负责的最后一题还没写出来。最终我的第一道题目是在同门的协助下写出来的,第四道题目赶快结束才写完,直接还没来得及运行用例就提交了。实际上最后一题我的思路是比较清晰的,但是在创建图和写DFS的时候花了太多的时间,还有就是写代码的时候,一定要思维先行,想清楚要干什么再写。下面我来带大家看看这四道题目:
2. First Problem
第一题叫做“豆油瓶”,题目类似于Leetcode 547 朋友圈。
2.1 题目描述:
抖音上每天有几亿用户,如果用户A和用户B互动不少于三次,我们就认为A和B属于豆油,如果A和B属于豆油,B和C属于豆油,那么A和C 也属于豆油。我们定义豆油瓶就是由直系和间接朋友所组成的群体。
给定一个N*N的矩阵M,代表抖音上所有用户的互动次数,如果M[i][j] = 5,那么第i个用户和第j个用户的互动次数就为5次,为0的话代表没有互动。对于i == j,即同一个用户,互动次数我们计为0。请你计算并输出发现的抖音上的豆油瓶的个数。
样例输入:
3
0 4 0
4 0 0
0 0 0
样例输出:2 (用户0和用户1的互动次数为4次,所以0和1组成了一个豆油瓶,用户2没有产生互动,所以单独为一个豆油瓶)
2.2. 解答:
这道题实质上就是求无向图的连通分量个数,所以我们用DFS来解答。不过也能用并查集来做。
思路是:1. 根据约束条件创建无向图 2. 求连通分量个数
var marked []bool var count int func DFS(v int, g [][]int) { fmt.Println("v", v, "marked", marked) marked[v] = true adjs := getAdjs(v, g) for _, adj := range adjs { if marked[adj] == false { DFS(adj, g) } } } func getAdjs(v int, g [][]int) []int { var adjs []int for i, elm := range g[v] { if elm != 0 { adjs = append(adjs, i) } } return adjs } func createGraph(comm [][]int, n int) [][]int { for i := 0; i < n; i++ { for j := 0; j < n; j++ { if comm[i][j] >= 3 { comm[i][j] = 1 } else { comm[i][j] = 0 } } } return comm } func solution(comm [][]int, n int) { g := createGraph(comm, n) fmt.Println(g) marked = make([]bool, n) count = 0 for i := 0; i < n; i++ { if marked[i] == false { DFS(i, g) count++ } } }
3. Second Problem
第三题对我来说是这几道题目中最难理解的一道题目。下面我们来看看吧。
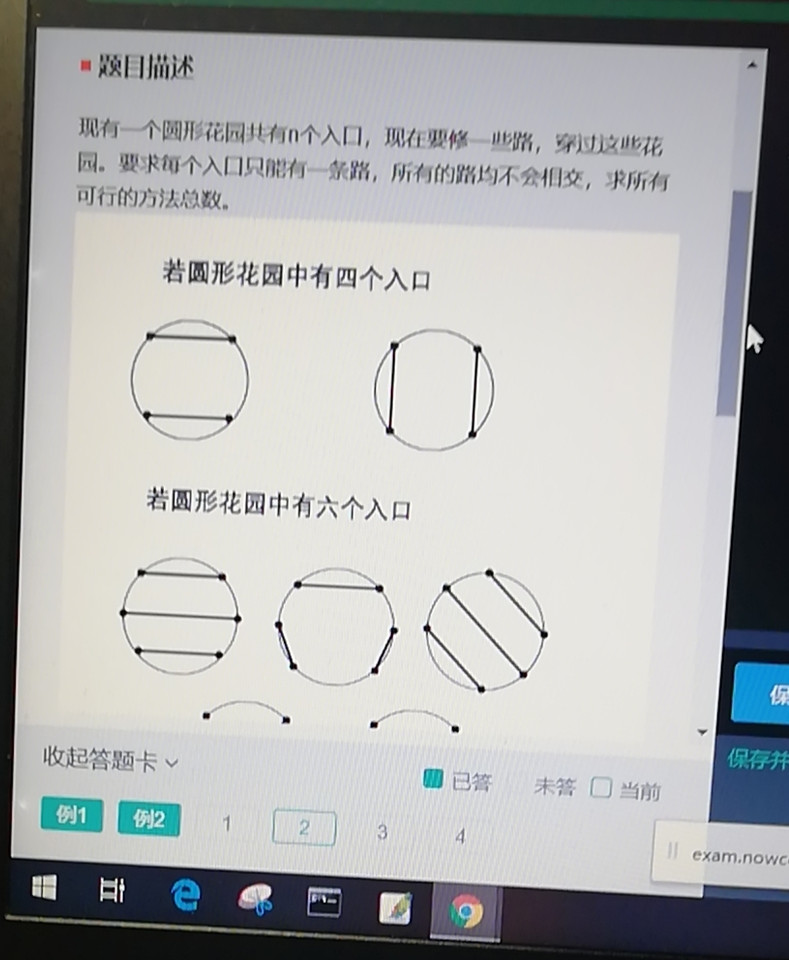
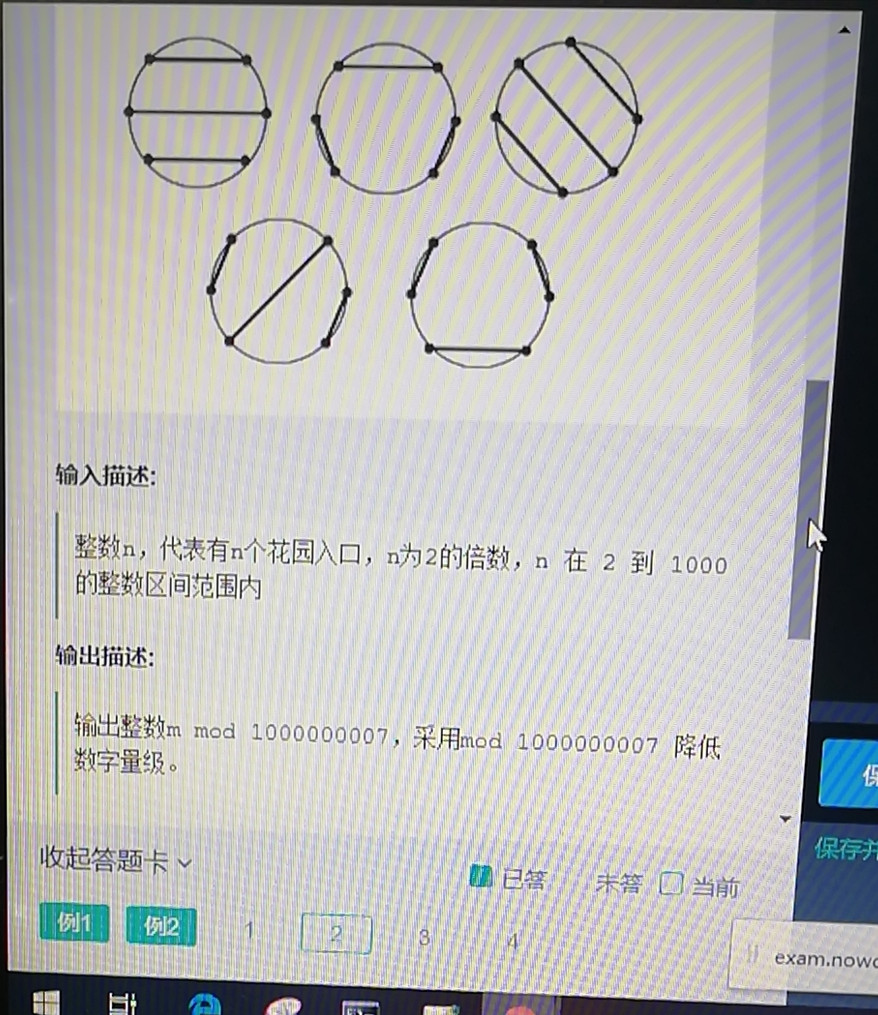
3.1 题目描述
现有一个圆形花园共有n个入口,现在要修一些路,穿过这个花园。要求每个路口只能有一条路,所有的路均不会相交,求所有可行的方法总数。输入输出如上图所示。
3.2 解答
这道题目,我真的是光完全理解题目就花了好久,侧面反映出我的智商有问题,还需要好好磨练。这道题是使用的是动态规划的思路,下面我来解答以下这道题目的思路。
我们先给每个入口从1开始编号,先假设6个入口的情况。对于1号口,可以连接的入口有 2,3,6号。

如果连接1,2,6个点的问题会被分解为2个点和4个点的问题。为什么?看下面的图,是不是很清晰。所以这种情况下的方法总数是F(2) * F(4)。为什么是乘法,因为这里不是独立的关系,是先定两个点,在这个基础上在计算4个点的情况。
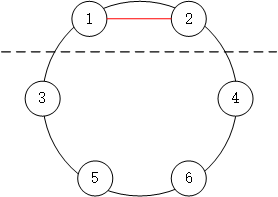
如果连接1,3,子问题的划分和上述讨论是类似的。因此总数也等于F(2) * F(4)

但是连接1,6的话,情况就不同了。这里1,6间的路把整个花园分成了两个部分,每个部分只有两个口,因此方法总数是F(2) * F(2)
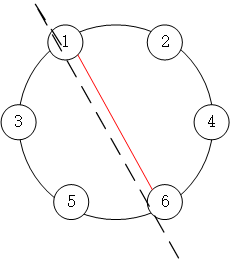
最后六个点的情况就等于以上几种情况相加,因此F(6) = F(2)*F(4) + F(2)*F(4) + F(2)*F(2) = 1*2 + 1*2 + 1 = 5
按说应该在多讨论几种情况,才能得出递推公式,但是时间有限,这里我就直接给出来:
对于第二项,F(i)*F(j),i+j = n-2。
//f[2m] = 2*f[2m-2]*f[2] + f[c1]*f[c2], c1+c2 = 2m-2 func solution(n int) int { m := make([]int, n+1) m[0] = 0 m[2] = 1 for i := 4; i <= n; i = i + 2 { tmp := 0 for j := 2; j <= i-2; j = j + 2 { tmp += m[i-2-j] * m[j] } m[i] = 2*m[i-2]*m[2] + tmp } return m[n] }
4. Third Problem
4.1 题目描述
 、
、4.2 解答
这道题应该是这四道题目,最简单的一道了,没有任何特殊的技巧。关键是理解题目的意思,和我们通常玩的2048不同,这里进行一次操作,整个矩阵都会朝目标方向移动,并且相邻会碰撞的两个数字会合并,并且两个数字只会触发一次合并,且优先合并移动方向顶端的位置。
对于行[ 2 2 2 2 ],向右移动后,该行变为,[ 0 0 4 4 ]。那么是如何变成这样的呢?
先进行合并操作,a[3] = a[3] + a[2],a[1] = a[1] + a[0]。之后行变为[ 0 4 0 4]。之后进行右移操作,即a[2] = a[1], a[1] = 0。右移之后,行变为[ 0 0 4 4 ]。
func Up(board [][]int) { for i := 0; i < 4; i++ { board[0][i] += board[1][i] board[2][i] += board[3][i] board[1][i] = board[2][i] board[2][i] = 0 board[3][i] = 0 } } func Down(board [][]int) { for i := 0; i < 4; i++ { // board[1][i] += board[0][i] board[3][i] += board[2][i] // board[2][i] = board[1][i] board[0][i] = 0 board[1][i] = 0 } } func Left(board [][]int) { for i := 0; i < 4; i++ { board[i][0] += board[i][1] board[i][2] += board[i][3] board[i][1] = board[i][2] board[i][2] = 0 board[i][3] = 0 } } func Right(board [][]int) { for i := 0; i < 4; i++ { board[i][3] += board[i][2] board[i][1] += board[i][0] board[i][2] = board[i][1] board[i][1] = 0 board[i][0] = 0 } } func solution(oper []int, board [][]int) [][]int { for i := 0; i < len(oper); i++ { switch oper[i] { case 1: Up(board) case 2: Down(board) case 3: Left(board) case 4: Right(board) } } return board }
5. Forth Problem
5.1 问题描述

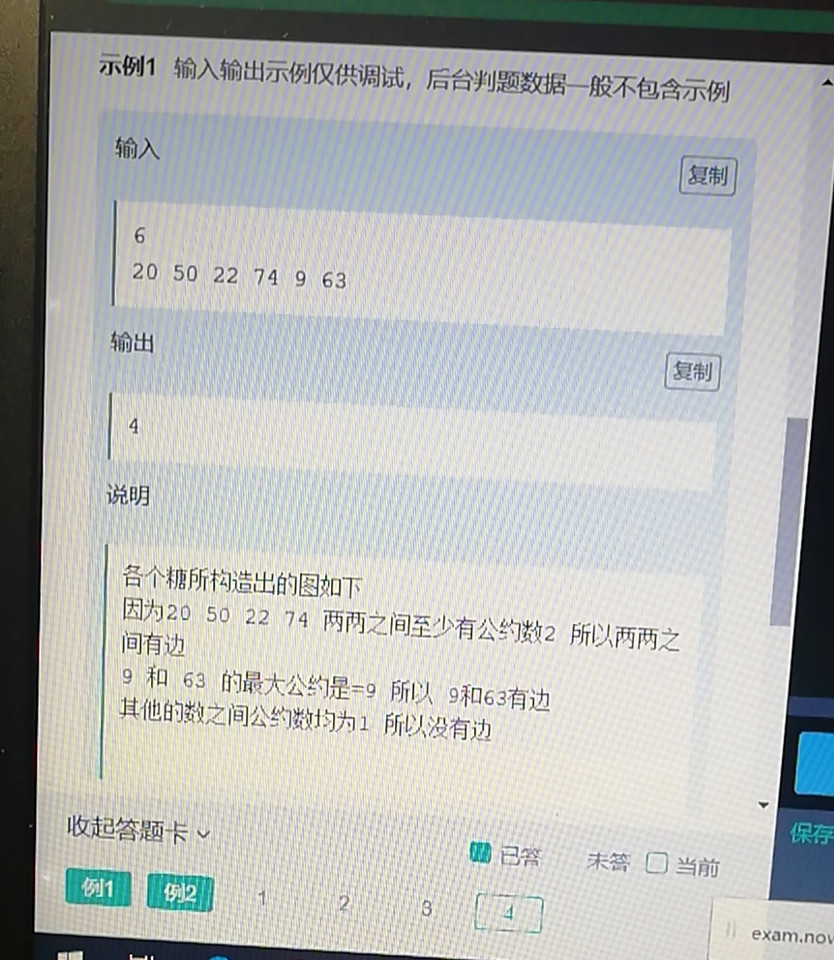
在漫天的星空里散落着一些糖果,他们各有各的甜度。有一些糖果之间会按照一定的规则有桥梁连接,好让你获得了这个糖果之后,可以去获得和该糖果相连的其他糖果。现在让你从一个糖果出发,去尽可能多的获取糖果。
我们将糖果编号 1 ... ... n。每个糖果的甜度记为a[i]。若糖果i和j的甜度的最大公约数>1。则糖果i和j之间有桥梁连接。
5.2 解答
这道题也是使用DFS进行求解,每个糖果是图的一个节点。满足约束条件的结点间有边相连。这道题实质上是求拥有最多节点的连通子图的节点个数。因此把第一个问题的代码修改以下就OK了。关键是设置一个变量max去存储最大值,和变量c1去存储当前连通子图的节点个数。
func createGraph(sweets []int) [][]int { n := len(sweets) graph := make([][]int, n) for i := 0; i < n; i++ { graph[i] = make([]int, n) for j := 0; j < n; j++ { graph[i][j] = 0 } } for i := 0; i < n; i++ { for j := i + 1; j < n; j++ { if GCD(sweets[i], sweets[j]) > 1 { graph[i][j] = 1 graph[j][i] = 1 } } } return graph } var marked []bool var count, max int //gcd(x, y) = gcd(y, x%y) func GCD(x, y int) int { for y != 0 { r := y y = x % y x = r } return x } func DFS(v int, g [][]int) { count++ marked[v] = true adjs := getAdjs(v, g) for _, adj := range adjs { if marked[adj] == false { DFS(adj, g) } } } func getAdjs(v int, g [][]int) []int { var adjs []int for i, elm := range g[v] { if elm != 0 { adjs = append(adjs, i) } } return adjs } func solution(n int, sweets []int) { graph := createGraph(sweets) marked = make([]bool, len(sweets)) for i := 0; i < n; i++ { if marked[i] == false { count = 0 DFS(i, graph) if count > max { max = count } } } }
6. 总结
这次笔试的惨败,反映出我数据结构和算法的薄弱(要达到对于任何数据结构的代码都烂熟于心的程度)。其次,是秋招准备的不充分。最后是智商的局限。牛客上很多人都AC了2道或者3道题目。总之任重而道远。