问题描述
给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。
不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
解答
既然数组是有序的，那么相同的元素肯定是连续排列的。这是一道典型的双指针（双下标）题目， 使用两个下标 i, j。i 从第二个元素开始遍历数组中的每一个元素， j 从第一个元素开始。 如果 i 指向的元素等于 j 指向的元素，i 指向下一个元素， j 依旧指向上一个元素。
注意这里是关键点， 否则 如果不等于， j 指向下一数字，并用 i 指向的元素覆盖 j 指向的元素。 j 全程只可能小于等于 i 。 j 的作用是遍历数组中的子序列。 让
我们来看个例子， 初始时，nums[ i ] = 2, nums[ j ] = 1, 不相等所以 j 加一指向 2 ， 这时发生了重复元素的赋值。i = j = 1 。
下一次循环开始， i = 2 ， j = 1。 nums[ i] = nums[ j ]， 所以 i 指向下一个元素。 而 j 依旧指向 2这个子序列的第一个元素。
循环直到 i 指向3，当然nums[ i ] != nums[ j] , 所以 j 指向子序列的下一个元素， 并使用 i 指向的值 3 覆盖 j 指向的 2。 这时数组变成了如下所示。
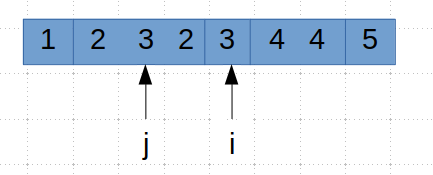
下次循环开始, i 指向下一个子序列的第一个数字4, 同样 nums[ i ] ! = nums [ j ]。 所以 j 加1后指向为2的子序列的下一个元素，然后将num[ i ] = 4 覆盖 num [ j ] = 2
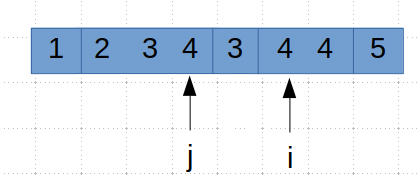
至此， 2这个子序列就已经遍历完成。我也就不在继续赘述。整个过程完成后的数组如下所示。
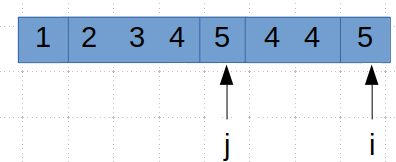
接下来我们在说说另一种特殊情况， 那就是数组中没有重复元素时， 通过分析这种情况，我们可以更好的理解 i 和 j 的变化究竟对于数组有什么影响！
在这种情况下， 子序列都只有一个元素。i = { j + 1 , j } , 也就是说 i 要么比 j 大 1, 要么等于 j 。
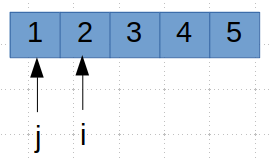
初始时， nums[ i ] = 1 不等于 nums [ j ] = 2， 所以 j 指向下一个元素， 并将nums [ i ] = 2 覆盖 nums [ j ] = 2。 值得注意的是这种情况下发生了相同元素的赋值，
这也是这个算法可优化的方向。接下来的每次循环都是同样的操作。记得上文说过的 j 指向的是子序列， 这里因为子序列长度为1， 所以 i 和 j 相差最大也为 1 。
到这里，这个算法也基本说明完毕了。由于我比较笨， 所以这道题的解法想了一早上，i 和 j 的变化使我困惑了很久，思考了很久，尝试了很多类型的用例，终于还
是想清楚了。总结一下， 通过这道题，我的收获是 双指针方法在许多数组的题目都有出现，需要好好掌握。其次， 持久的思考能力至关重要。