快速排序(quick sort)的特点是分块排序,也叫划分交换排序(partition-exchange sort)
代码实现方式可以有这么几种:
- 拼接结果
- 左右相互交换
- 快慢指针
1. 拼接结果
# Python3
class Solution:
def quicksort(self, nums):
# 当为 0 个或 1 个时,肯定有序,直接返回
if len(nums) < 2:
return nums
else:
# 选择第一位作为中位数
mid = nums[0]
less = [num for num in nums[1:] if num <= mid]
greater = [num for num in nums[1:] if num > mid]
return self.quicksort(less) + [mid] + self.quicksort(greater)
这种方式最直观,最好理解,但效率不高。为了找出大于和小于中位数的元素,循环遍历了 2 次
做一点小小的修改,改为一次遍历:
class Solution:
def quicksort(self, nums):
if len(nums) < 2:
return nums
else:
mid = nums[0]
less, greater = self.partition(nums, mid)[0], self.partition(nums, mid)[1]
return self.quicksort(less) + [mid] + self.quicksort(greater)
def partition(self, nums, mid):
less, greater = [], []
for num in nums[1:]:
if num <= mid:
less.append(num)
else:
greater.append(num)
return less, greater
优化后,运行时间降低了,但空间使用还很高,每次递归都额外需要 2 个平均长度为 ¼ n 的数组
1 + 2 ... + n-1 + n = ((n + 1) * n ) / 2
平均值 = ((n + 1) * n ) / 2 / n = (n + 1) / 2
两个数组平分平均值: (n + 1) / 2 / 2 ≈ 1/4 n
2. 左右相互交换
其实可以不使用额外空间,直接操作原数组。选择一个基准值,将小于它和大于它的元素相互交换。
class Solution:
def quicksort(self, nums):
self.quick_sort(nums, 0, len(nums) - 1)
def quick_sort(self, nums, start, end):
# end - start < 1
if start >= end:
return
# 每次使用最后一个数作为基准值
pivot_index = end
pivot = nums[pivot_index]
left, right = start, end - 1
while left < right:
# 左边跳过所有小于基准值的元素
while nums[left] <= pivot and left < right:
left += 1
# 右边跳过所有大于基准值的元素
while nums[right] > pivot and left < right:
right -= 1
# 交换
nums[left], nums[right] = nums[right], nums[left]
# 此时左右指针重合(left == right),其指向元素可能大于基准值
if nums[left] > pivot:
nums[left], nums[pivot_index] = nums[pivot_index], nums[left]
# 使 left 始终作为较大区间的第 1 个元素
else:
left += 1
self.quick_sort(nums, start, left - 1)
# pivot 不一定在中间,所以包含 left
self.quick_sort(nums, left, end)
使用此种方式,最好要将开头(或末尾)的元素设为基准值。如果使用中间元素,最后也交换到开头(或末尾),否则将考虑大量场景。
排序过程:
[6 5 3 1 8 7 2 4]
↑ ↑ ^
[2 5 3 1 8 7 6 4]
↑ ↑ ^
[2 1 3 5 8 7 6 4]
↑↑ ^
[2 1 3 4 8 7 6 5]
^
[2 1 3][4 8 7 6 5]
nums[left] <= pivot 时:
[6 7 3 4 8 1 2 5]
↑ ↑ ^
[2 7 3 1 8 1 6 5]
↑ ↑ ^
[2 1 3 4 8 7 6 5]
↑↑ ^
[2 1 3 4][8 7 6 5]
3. 快慢指针
上面这种方式其实使用两个相向指针,也可以使用同向快慢指针实现元素交换。
class Solution:
def quicksort(self, nums):
import random
def quick_sort(left, right):
# right - left < 1
if left >= right:
return
# 随机选择一个元素作为 pivot
pivot_index = random.randint(left, right)
pivot = nums[pivot_index]
# 1. 将中位数与末尾数交换,便于操作
nums[pivot_index], nums[right] = nums[right], nums[pivot_index]
# 2. 使用快慢指针,将所有小于中位数的元素移动到左边
store_index = left
for i in range(left, right):
if nums[i] <= pivot:
nums[store_index], nums[i] = nums[i], nums[store_index]
store_index += 1
# 3. store_index 位置元素肯定大于等于 pivot,所以交换
nums[right], nums[store_index] = nums[store_index], nums[right]
# 因为 pivot 在中间,所以减 1
quick_sort(left, store_index - 1)
# 因为 pivot 在中间,所以加 1
quick_sort(store_index + 1, right)
quick_sort(0, len(nums) - 1)
排序过程:
[6 5 3 1 8 7 2 4]
↑↑ ^
[6 5 3 1 8 7 2 4]
↑ ↑ ^
[3 5 6 1 8 7 2 4]
↑ ↑ ^
[3 1 6 5 8 7 2 4]
↑ ↑ ^
[3 1 2 5 8 7 6 4]
↑ ^
[3 1 2 4 8 7 6 5]
^
[3 1 2][4][8 7 6 5]
随机选择可以增加每次选择的基准值为中位数的几率
时间复杂度
最坏时间复杂度
每次基准值都是最大 (或最小)值时,所需递归次数最多,有两种情况:
- 数组有序时,每次使用最后 1 位(或第 1 位)作为基准值
1 2 3 4 5 6 7 8
^
1 2 3 4 5 6 7 [8]
^
1 2 3 4 5 6 [7]
^
1 2 3 4 5 [6]
^
1 2 3 4 [5]
^
1 2 3 [4]
^
1 2 [3]
^
1 [2]
^
[1]
- 随机选择时,每次选择到最大(或最小)的一位
6 7 3 4 8 1 2 5
^
6 7 3 4 1 2 5 [8]
^
6 3 4 1 2 5 [7] 8
^
3 4 1 2 5 [6] 7 8
^
3 4 1 2 [5] 6 7 8
^
3 1 2 [4] 5 6 7 8
^
1 2 [3] 4 5 6 7 8
^
1 [2] 3 4 5 6 7 8
^
[1] 2 3 4 5 6 7 8
此时递归次数为 n + 1,平均每次排序 ½ n 个数。所以最坏时间复杂度:O(n^2)。
最好时间复杂度
如果每次选择中位数作为基准值,递归次数会减少么?其实不会减少,但递归中遍历的次数会减少。如果每层遍历看成 n 次的话,可以用下面的这个图表示:
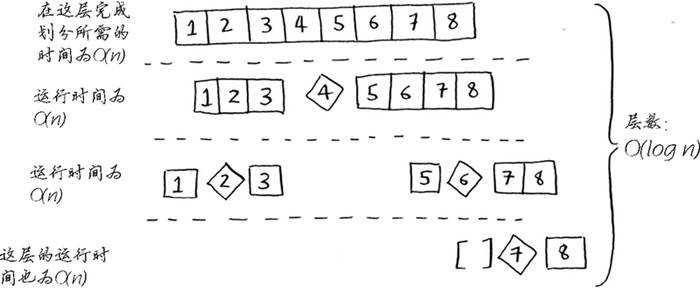
所以最好时间复杂度为:O(n * log n)
平均时间复杂度
最坏时间复杂度的情况很少见,所以平均时间复杂度就是最好时间复杂度 O(n * log n)
空间复杂度
每次递归均会使用额外空间,所以空间复杂度跟递归次数有关。
最坏时间复杂度时,最坏空间复杂度也为 O(n)。最好时间复杂度时时,虽然递归没有减少,但当只有 1 个或 0 个元素时,没有使用额外空间,直接返回,所以最好空间复杂度为 O(log n)。平均时间复杂度也为 O(log n)。
第 1 种实现因为使用额外数组,最坏空间复杂度为 O(n^2),最好空间复杂度为 O(n * log n),
测试代码
import logging
logging.basicConfig(level=logging.INFO)
def main():
# nums = [3, 2, 1, 5, 6, 4]
# 针对第 1 种
print(Solution().quicksort(nums))
# 针对第 2、3 种
# Solution().quicksort(nums)
# print(nums)
if __name__ == '__main__':
main()
测试用例
[3, 2, 1, 5, 6, 4]
[3, 2, 1, 5, 6, 4, 4, 1]
[6, 5, 3, 1, 8, 7, 2, 4]
[]