分段树（segment tree）的实现 —— 强化学习中 "优先级回放机制" 的重要组成部分

分段树（segment tree）是强化学习中 "优先级回放机制" 的重要组成部分。本文针对分段树（segment tree）的一个开源版本的实现来进行分析，代码地址：

https://gitee.com/devilmaycry812839668/Rainbow/blob/master/memory.py

Transition_dtype = np.dtype(
    [('timestep', np.int32), ('state', np.uint8, (84, 84)), ('action', np.int32), ('reward', np.float32),
     ('nonterminal', np.bool_)])
blank_trans = (0, np.zeros((84, 84), dtype=np.uint8), 0, 0.0, False)


# Segment tree data structure where parent node values are sum/max of children node values
class SegmentTree():
    def __init__(self, size):
        self.index = 0
        self.size = size
        self.full = False  # Used to track actual capacity
        self.tree_start = 2 ** (size - 1).bit_length() - 1  # Put all used node leaves on last tree level
        self.sum_tree = np.zeros((self.tree_start + self.size,), dtype=np.float32)
        self.data = np.array([blank_trans] * size, dtype=Transition_dtype)  # Build structured array
        self.max = 1  # Initial max value to return (1 = 1^ω)

    # Updates nodes values from current tree
    def _update_nodes(self, indices):
        children_indices = indices * 2 + np.expand_dims([1, 2], axis=1)
        self.sum_tree[indices] = np.sum(self.sum_tree[children_indices], axis=0)

    # Propagates changes up tree given tree indices
    def _propagate(self, indices):
        parents = (indices - 1) // 2
        unique_parents = np.unique(parents)
        self._update_nodes(unique_parents)
        if parents[0] != 0:
            self._propagate(parents)

    # Updates values given tree indices
    def update(self, indices, values):
        self.sum_tree[indices] = values  # Set new values
        self._propagate(indices)  # Propagate values
        current_max_value = np.max(values)
        self.max = max(current_max_value, self.max)

    # Propagates single value up tree given a tree index for efficiency
    def _propagate_index(self, index):
        parent = (index - 1) // 2
        left, right = 2 * parent + 1, 2 * parent + 2
        self.sum_tree[parent] = self.sum_tree[left] + self.sum_tree[right]
        if parent != 0:
            self._propagate_index(parent)

    # Updates single value given a tree index for efficiency
    def _update_index(self, index, value):
        self.sum_tree[index] = value  # Set new value
        self._propagate_index(index)  # Propagate value
        self.max = max(value, self.max)

    def append(self, data, value):
        self.data[self.index] = data  # Store data in underlying data structure
        self._update_index(self.index + self.tree_start, value)  # Update tree
        self.index = (self.index + 1) % self.size  # Update index
        self.full = self.full or self.index == 0  # Save when capacity reached
        self.max = max(value, self.max)

    # Searches for the location of values in sum tree
    def _retrieve(self, indices, values):
        children_indices = (indices * 2 + np.expand_dims([1, 2], axis=1))  # Make matrix of children indices
        # If indices correspond to leaf nodes, return them
        if children_indices[0, 0] >= self.sum_tree.shape[0]:
            return indices
        # If children indices correspond to leaf nodes, bound rare outliers in case total slightly overshoots
        elif children_indices[0, 0] >= self.tree_start:
            children_indices = np.minimum(children_indices, self.sum_tree.shape[0] - 1)
        left_children_values = self.sum_tree[children_indices[0]]
        successor_choices = np.greater(values, left_children_values).astype(
            np.int32)  # Classify which values are in left or right branches
        successor_indices = children_indices[
            successor_choices, np.arange(indices.size)]  # Use classification to index into the indices matrix
        successor_values = values - successor_choices * left_children_values  # Subtract the left branch values when searching in the right branch
        return self._retrieve(successor_indices, successor_values)

    # Searches for values in sum tree and returns values, data indices and tree indices
    def find(self, values):
        indices = self._retrieve(np.zeros(values.shape, dtype=np.int32), values)
        data_index = indices - self.tree_start
        return (self.sum_tree[indices], data_index, indices)  # Return values, data indices, tree indices

    # Returns data given a data index
    def get(self, data_index):
        return self.data[data_index % self.size]

    def total(self):
        return self.sum_tree[0]

分段树的具体逻辑结构如下：（原图地址：https://www.cnblogs.com/pinard/p/9797695.html）

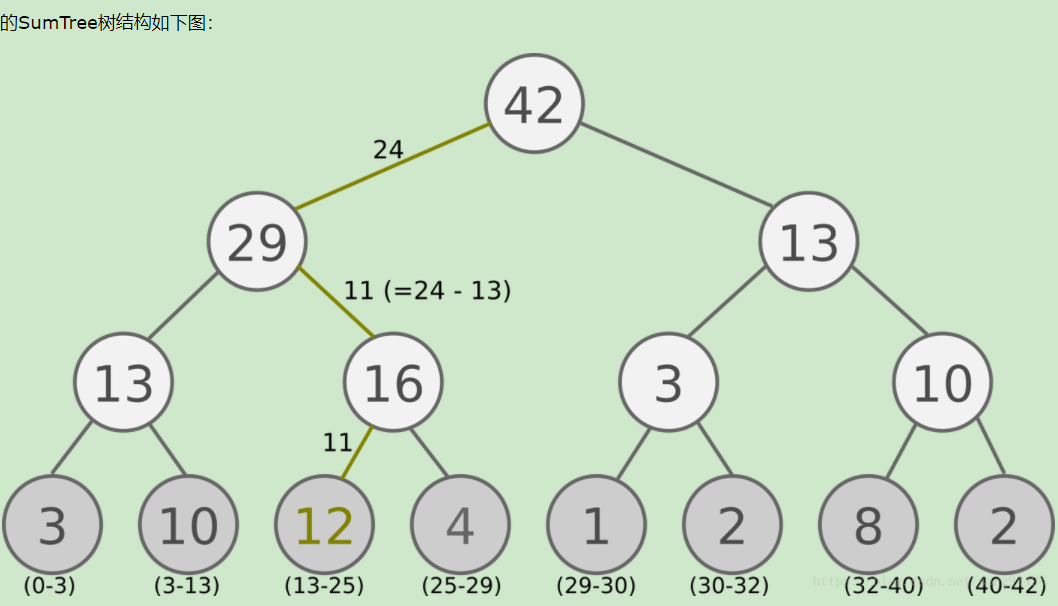
这个segment tree可以分为两个部分，一个部分是权重（待检索数据的权重）的索引部分，另一部分是数据（待检索数据）的存储部分。

上图中的数据部分（待检索的数据）就是下图的表示：

权重（待检索数据的权重）的索引部分为：

 ===================================================

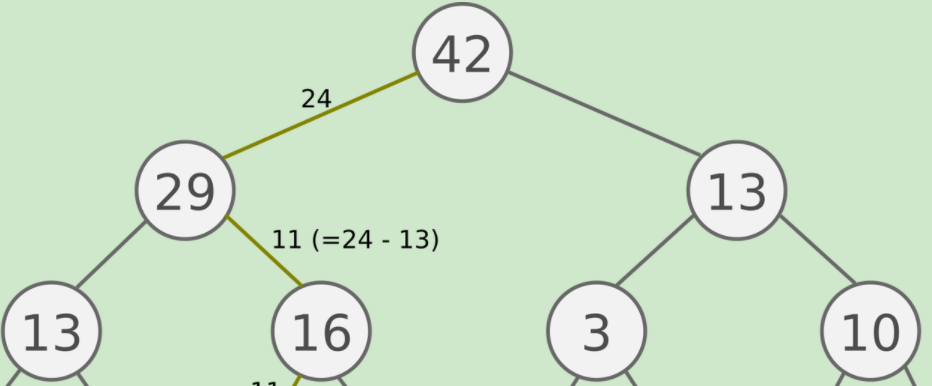
代码分析：

在__init__ 函数部分：

self.size = size   #指的是需要存储的数据（待检索的数据）的最多个数。

self.full  #是记录存储的数据个数有没有达到最多个数的要求，即是否存储满。

self.tree_start = 2 ** (size - 1).bit_length() - 1 

#比较不好理解的部分，如果存储size个数据，那么需要编号的话就是0 到 size-1 ，

#最大的编号size-1的二进制表示的长度为 (size - 1).bit_length()，

# (size - 1).bit_length() 长的二进制位所能表示的最多个数编号为 0 到 2 ** (size - 1).bit_length() - 1

形象的说，看下图：

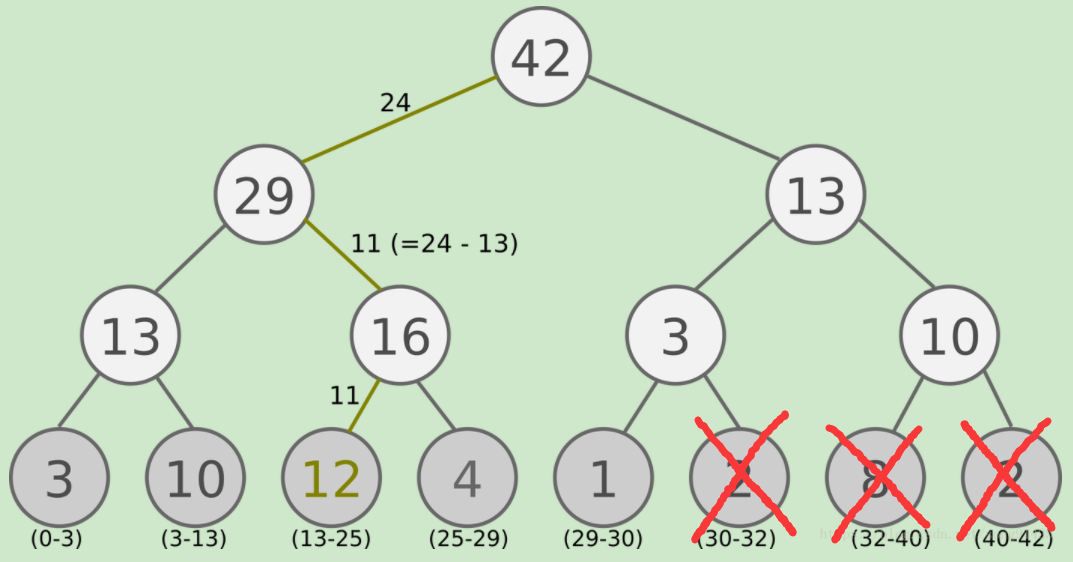
 如果我们有5个数据，而这5个数据全部为同一层的叶子节点，那么构建一个二叉树后如果非叶子节点的部分为满二叉树，那么非叶子节点的部分为 7。

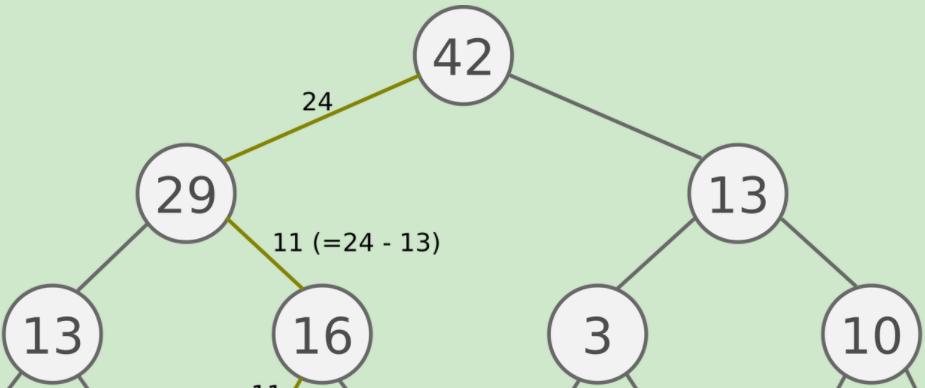
 非叶子节点，也是分段树中索引节点的个数，在size=5时，个数为7 。

self.sum_tree = np.zeros((self.tree_start + self.size,), dtype=np.float32)

 生成一个float数组矩阵，大小为索引节点个数 self.tree_start 与 数据节点个数 self.size 的和。其中，索引节点和数据节点存储的都是权重值。

segment tree中存储的是待检索数据的权重，其中叶节点是直接存储的待检索数据的权重，非叶节点则存储的是子节点权重之和。而self.data 则是存储的待检索数据，数据的数据类型为自定义的 Transition_dtype

self.data = np.array([blank_trans] * size, dtype=Transition_dtype)

 self.max = 1 #初始化segment tree时新存入节点的默认权重值，初始化为 1 

 =====================================================

 单个数据的插入，并更新segment tree中对应的权重值，并对与其相关的上层节点的权重值进行更新。

    # Propagates single value up tree given a tree index for efficiency
    def _propagate_index(self, index):
        parent = (index - 1) // 2
        left, right = 2 * parent + 1, 2 * parent + 2
        self.sum_tree[parent] = self.sum_tree[left] + self.sum_tree[right]
        if parent != 0:
            self._propagate_index(parent)

    # Updates single value given a tree index for efficiency
    def _update_index(self, index, value):
        self.sum_tree[index] = value  # Set new value
        self._propagate_index(index)  # Propagate value
        self.max = max(value, self.max)

    def append(self, data, value):
        self.data[self.index] = data  # Store data in underlying data structure
        self._update_index(self.index + self.tree_start, value)  # Update tree
        self.index = (self.index + 1) % self.size  # Update index
        self.full = self.full or self.index == 0  # Save when capacity reached
        self.max = max(value, self.max)

由于我们的数据是存储在 self.data 中， 而数据对应的权重值是存储在segment tree中。

self.index 是 self.data 中当前可以写入的位置的索引号。同时，self.index+self.tree_start 也是对应权重在 self.sum_tree 中的索引位置。

def append: 中的输入参数value则是数据data对应的权重值。也就是说self.sum_tree中索引号self.index+self.tree_start中所存储的权重值为value。

def _propagate_index(self, index)  函数：

更新segment tree中子节点的父节点权重值，segment tree中索引为index的节点的父节点的索引为  parent = (index - 1) // 2

而index节点的父节点的子节点中的左右节点分别为： left, right = 2 * parent + 1, 2 * parent + 2

 当然，index节点的左右子节点中也必然包括index节点。

self.sum_tree[parent] = self.sum_tree[left] + self.sum_tree[right]

根据左右子节点的权重更新父节点的权重值。 

if parent != 0:
    self._propagate_index(parent)

迭代修改父节点的权重值，直到修改到根节点，即索引号为0的节点。

def _update_nodes(self, indices):

def _update_nodes(self, indices):

def update(self, indices, values):

一次性为多个节点修改权重值，具体类似于插入单个节点。

===========================================================

检索操作，在segment_tree中检索多个值（values）的索引号，并将其存入 indices 中。

检索操作应该是segment_tree的精髓部分，segment_tree 最重要的一个功能就是按照self.data中元素所对应的self.sum_tree中的权重值进行随机采样。

indices = self._retrieve(np.zeros(values.shape, dtype=np.int32), values)

    def _retrieve(self, indices, values):
        children_indices = (indices * 2 + np.expand_dims([1, 2], axis=1))  # Make matrix of children indices
        # If indices correspond to leaf nodes, return them
        if children_indices[0, 0] >= self.sum_tree.shape[0]:
            return indices
        # If children indices correspond to leaf nodes, bound rare outliers in case total slightly overshoots
        elif children_indices[0, 0] >= self.tree_start:
            children_indices = np.minimum(children_indices, self.sum_tree.shape[0] - 1)
        left_children_values = self.sum_tree[children_indices[0]]
        successor_choices = np.greater(values, left_children_values).astype(
            np.int32)  # Classify which values are in left or right branches
        successor_indices = children_indices[
            successor_choices, np.arange(indices.size)]  # Use classification to index into the indices matrix
        successor_values = values - successor_choices * left_children_values  # Subtract the left branch values when searching in the right branch
        return self._retrieve(successor_indices, successor_values)

children_indices = (indices * 2 + np.expand_dims([1, 2], axis=1))

 indices ，多个值的索引，children_indices 为indices所对应的父节点下的左右子节点的索引矩阵，0行（matrix的0行）为所有左子节点的索引值，1行（matrix的1行）为所有右子节点的索引值。这里初始化时多个值的初始索引均设置为根节点，即0号节点。

 children_indices[0, 0] >= self.sum_tree.shape[0]  子节点索引号最小的，即children_indices[0, 0] （因为indices中索引值为从小到大顺序排列），如果最小索引值大于self.sum_tree的长度则表示当前节点（即indices节点）为叶子节点。

 

 该部分代码对应的情形如下：

children_indices[0, 0] >= self.tree_start    如果索引号最小的节点小于segment tree的非叶子节点个数，那么子节点children_indices必然是叶子节点。

但是在该种情况下，会出现indices子节点不为叶子节点，该种情况下会有部分子节点不属于segment tree，如上图中的红叉部分节点（这里特指第一个红叉的点）。

第一个红叉的点需要被排除掉，因为第一个红叉点的索引号已经超出了segment tree中所能表示的叶节点的范围。其实，该种情况极难发生，因为不对次情况做处理的话也是会在下一步中只考虑对应的左子节点，因为待检索的权重值必然小于左子节点所对应的权重值，因此不对后续结果有影响。但是由于极小概率下浮点数表示的精度问题会导致将第一个红叉点也加入到考虑范围内，因此对该种情况进行特殊处理。

 如果查找的权重值value大于左子节点的权重值则下一个查找的节点为右子节点。如果下次迭代从右子节点开始查找对应的权重值，则需要将待查找的权重value减去左子节点的权重。

self._retrieve(successor_indices, successor_values)

 反复迭代查找权重值，直到达到叶子节点。

参考文献：

https://www.cnblogs.com/pinard/p/9797695.html