coursera机器学习笔记神经网络，初识篇

#对coursera上Andrew Ng老师开的机器学习课程的笔记和心得；

#注:此笔记是我自己认为本节课里比较重要、难理解或容易忘记的内容并做了些补充，并非是课堂详细笔记和要点；

#标记为<补充>的是我自己加的内容而非课堂内容，参考文献列于文末。博主能力有限，若有错误，恳请指正；

#---------------------------------------------------------------------------------#

神经网络的类型：感知机(单层)，多层神经网络；

<补充>：感知机(perceptron)是神经网络和支持向量机的基础，基本模型为:f(x)= sign(g(X))，sign为符号函数, x为输入向量，w为权值向量，b为bias；

；

g(X)可以是线性函数，也可以是sigmoid函数等；

#---------------------------------------------------------------------------------#

神经网络基本模型：

，

每一个单元有一定数量的实值输入，产生单一的实值输出(可以是其他很多单元的输入)；

神经网络的符号标记：a_i^(j) - activation of unit i in layer j ；Ɵ^(j) - matrix of parameters controlling the function mapping from layer j to layer j + 1；

j是指第几层，i指第几个节点，a_i^(j)指由前一层得到的输出值，并作为下一层的输入值；Ɵ^(j)是这一层通往为下一层的a_i^(j)的系数；

每个节点的计算公式：

；

；

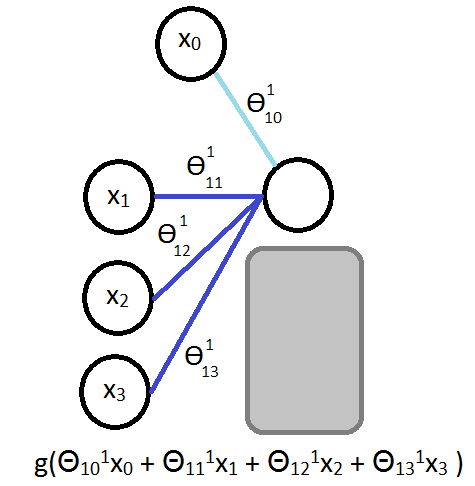• Ɵ₁₃¹ = means
  • 1 - we're mapping to node 1 in layer l+1
  • 3 - we're mapping from node 3 in layer l
  • 1 - we're mapping from layer 1

注！神经网络每个节点的输出并不是概率值，故没层的节点值之和不必等于1，如a₁⁽³⁾+a₂⁽³⁾+a₃⁽³⁾ != 1.

#---------------------------------------------------------------------------------#

<补充>：适合神经网络学习的问题需满足下列条件

1，实例是用很多“属性-值”对表示的；

2，目标函数的输出可能是离散值、实数值或若干值组成的向量；

3，训练数据可能包含错误(ANN有很好的健壮性)；

4，可容忍长时间的训练(ANN需要较长的训练时间)；

5，可能需要快速秋初目标函数值(ANN训练时间长，但预测所需时间很短，如无人驾驶)；

6，人类能否理解学到的目标函数是不重要的(ANN学习到的权值经常是人难以理解的)；

#---------------------------------------------------------------------------------#

神经网络实例：用神经网络来表征某些函数。

注!两层深度(两个隐藏层)的神经网络就可以表示所有的布尔函数。

<补充>：每个有界的连续函数可以有一个两层的网络以任意小误差逼近；

<补充>：任意函数可以被一个有三层单元的网络以任意精度逼近；

一个好例子：如何用NN来表示XOR函数？

#---------------------------------------------------------------------------------#

参考文献:

《统计学习方法》，李航著；

《machine learning》, by Tom Mitchell；

couresra课程: standford machine learning, by Andrew Ng；