#对coursera上
#注:此笔记是我自己认为本节课里比较重要、难理解或容易忘记的内容并做了些补充,并非是课堂详细笔记和要点;
#标记为<补充>的是我自己加的内容而非课堂内容,参考文献列于文末。博主能力有限,若有错误,恳请指正;
#---------------------------------------------------------------------------------#
<补充>支持向量机方法的三要素(若不了解机器学习模型、策略、算法的具体意义,可参考机器学习三要素)
基本模型:间隔最大的线性分类器;若用上核技巧,成为实质上的非线性分类器;
学习策略:间隔最大化,可形式化为一个求解凸二次规划的问题;
学习算法:求解凸二次规划的最优化算法,如序列最小最优算法(SMO);
#---------------------------------------------------------------------------------#
由logistic regression引出SVM
z=ΘTx
预测函数: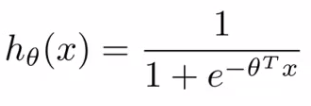 ;
;
logistic函数的图形:
 ;
;
当ΘTx 远大于0时,hθ(x)接近于0;
logistic回归的cost function:
![]()
![]() ;
;
当y=1时,上式变为-log(1 + e-z),见图形
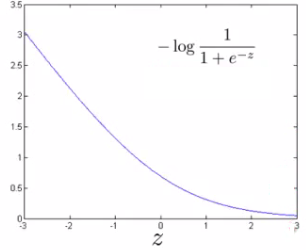 ;
;
SVM的cost function对logistic回归的cost function做了改变,当y=1时,SVM的cost function记为cost1(θT x),分为两部分(见下图紫线),当z>1时cost1(ΘTx)=0,当z<1时cost1(ΘTx)是条直线。这样做有两个好处,一是计算更快(从计算logistic函数转变为计算直线函数),二是更有利于后来的优化;
 ;
;
同理对y=0时做同样的处理,得到cost0(θT x),下图紫线。
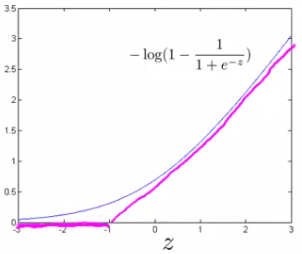 ;
;
由此我们得到cost0(θT x)和cost1(ΘTx):
 ;
;
由此我们从最小化logistic回归的cost function:
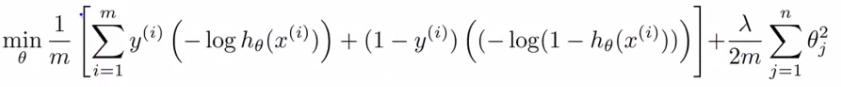 ,
,
得到下式:
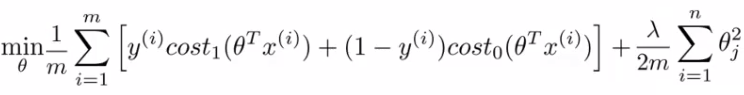 ;
;
再令C=1/λ,去掉1/m(m是常数,不影响计算优化结果),得到最终SVM的cost function:
 ;
;
#---------------------------------------------------------------------------------#
Large margin intuition
再来看SVM的cost0(θT x)和cost1(ΘTx):
 ;
;
注意:SVM wants a bit more than that - doesn't want to *just* get it right, but have the value be quite a bit bigger than zero
- Throws in an extra safety margin factor
对于训练数据,SVM不仅要求是分的对,而且还有额外的间隔条件来保证分的“好”;
 ;
;
- The green and magenta lines are functional decision boundaries which could be chosen by logistic regression
- But they probably don't generalize too well
- The black line, by contrast is the the chosen by the SVM because of this safety net imposed by the optimization graphMathematically, that black line has a larger minimum distance (margin) from any of the training examples
- More robust separator
- By separating with the largest margin,you incorporate robustness into your decision making process
<补充>什么是支持向量support vector?
下图中两个支撑着中间的 gap 的超平面,它们到中间的纯红线separating hyper plane 的距离相等,即我们所能得到的最大的 geometrical margin,而“支撑”这两个超平面的必定会有一些点,而这些“支撑”的点便叫做支持向量Support Vector。

C的选择对SVM的影响
C选的合适时,
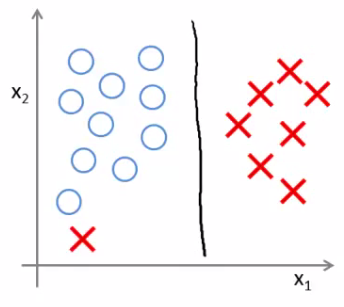 ;
;
C太大时造成过拟合(紫线),
 ;
;
<补充>最大间隔分离超平面存在唯一性:若训练数据线性可分(这是前提),则可将训练数据的样本点完全正确分开的最大间隔分离超平面存在且唯一;
#---------------------------------------------------------------------------------#
Kernels
<补充>当训练数据线性可分或近似线性可分时,通过间隔最大化,学习一个线性分类器;当训练数据线性不可分时,使用核技巧(kernel trick),学习非线性分类器;

<补充>核函数(kernel function)表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。通过使用核函数可以学习非线性支持向量机,等价于隐式地在高维空间的特征空间中学习线性支持向量机;也就是说,在核函数K(x,z)给定的条件下,可以利用解线性分类问题的方法去求解非线性分类问题的支持向量机。学习是隐式的在特征空间进行的,不需要显式地定义特征空间和映射函数。这样的技巧称作核技巧;
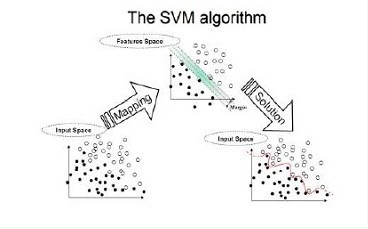
几个常用核函数
Gaussian kernel(使用最多的):Need to define σ (σ2);
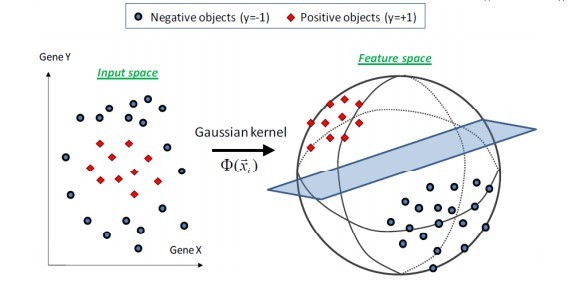 ;
;
linear kernel:no kernel;
others:Polynomial Kernel,String kernel,Chi-squared kernel...
#---------------------------------------------------------------------------------#
Logistic regression vs. SVM
If n (features) is large vs. m (training set)
- e.g. text classification problem
- Feature vector dimension is 10 000
- Training set is 10 - 1000
-
Then use logistic regression or SVM with a linear kernel
If n is small and m is intermediate
- n = 1 - 1000
- m = 10 - 10 000
- Gaussian kernel is good
If n is small and m is large
- n = 1 - 1000
- m = 50 000+
-
- SVM will be slow to run with Gaussian kernel
-
- In that case
-
- Manually create or add more features
- Use logistic regression of SVM with a linear kernel
-
Logistic regression and SVM with a linear kernel are pretty similar
- Do similar things
- Get similar performance
A lot of SVM's power is using diferent kernels to learn complex non-linear functions
For all these regimes a well designed NN should work
- But, for some of these problems a NN might be slower - SVM well implemented would be faster
SVM has a convex optimization problem - so you get a global minimum
#---------------------------------------------------------------------------------#
参考文献
《统计学习方法》,李航著
理解SVM的三层境界-支持向量机通俗导论,July、pluskid著
standford machine learning, by Andrew Ng