752. 打开转盘锁
描述:

思路:广度优先。对于求最短的,一般都是广度。

// 计算从起点 start 到终点 target 的最近距离 int BFS(Node start, Node target) { Queue<Node> q; // 核心数据结构 Set<Node> visited; // 避免走回头路 q.offer(start); // 将起点加入队列 visited.add(start); int step = 0; // 记录扩散的步数 while (q not empty) { int sz = q.size(); /* 将当前队列中的所有节点向四周扩散 */ for (int i = 0; i < sz; i++) { Node cur = q.poll(); /* 划重点:这里判断是否到达终点 */ if (cur is target) return step; /* 将 cur 的相邻节点加入队列 */ for (Node x : cur.adj()) if (x not in visited) { q.offer(x); visited.add(x); } } /* 划重点:更新步数在这里 */ step++; } }
754. 到达终点数字
描述:

思路; 从1到N一直累加, 直到SUM==TARGET, 或SUM减TARGET为正偶数. 因为在第n步往回走一次,SUM就会减少2n, 所以他们的差必须是偶数才能到.
763. 划分字母区间
描述:

思路:先统计每个字符的区间(遍历一遍)。然后对区间进行合并(按照第一个坐标排序,贪心)。
765. 情侣牵手
描述:

思路:

class Solution(object): def minSwapsCouples(self, row): """ 每两个座位成一对,假定左边的人都是合法的不变,如果TA右边的人与TA匹配则 跳过,不匹配则找到TA的匹配对象的与TA右边的人交换。 """ def find_another(n): if n % 2 == 0: return n + 1 else: return n - 1 c = 0 for i in range(0, len(row), 2): p1 = row[i] p2 = find_another(p1) if row[i+1] != p2: j = row.index(p2) row[i+1], row[j] = row[j], row[i+1] c += 1 return c
767. 重构字符串
描述:

思路:将每个字符和出现的次数存入堆。每次去前两个大的元素,然后和前面一个比对,吧不同的输出,然后更新次数再次入堆。
一定要注意堆的性质。看到题学会分析堆的可用性
768. 最多能完成排序的块 II
描述:

思路:
769. 最多能完成排序的块
类似于上题。
773. 滑动谜题
描述:

思路:广度优先;;;;A*搜索。
779. 第K个语法符号
描述:

思路:找规律。
781. 森林中的兔子
描述:

思路:
//要想使得兔子数量最小,那么尽量将报同样数量的视为同一颜色,但为了不矛盾,需要使用map记录对应颜色兔子最大的出现次数 报0的兔子一定是独一无二的直接++ var numRabbits = function(answers) { let map = new Map(), res = 0; for (let a of answers) { if (a == 0) { res++; } else if (!map.has(a)) { res += (1 + a); map.set(a, a); } else { map.set(a, map.get(a) - 1); if (map.get(a) == 0) { map.delete(a); } } } return res; };
785. 判断二分图
描述:

思路:图的遍历。遇到一个节点,如果是对立色,继续便利,如果是相同,flase.如果没眼色,将其颜色改变为对立色。
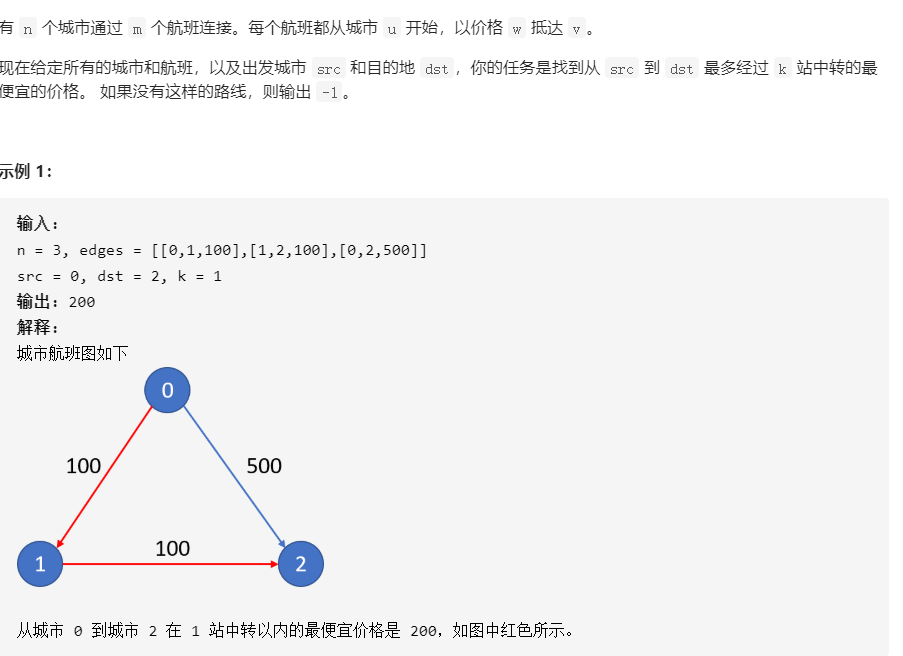
787. K 站中转内最便宜的航班
描述:
思路:

class Solution { public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) { int[][] g = new int[n][n];//记录的是目的地 for(int[] f : flights) { g[f[0]][f[1]] = f[2]; } PriorityQueue<int[]> heap = new PriorityQueue<>((a,b)->a[0] - b[0]); //集合的参数是一个comparator的lambda表达式,默认升序 heap.offer(new int[]{0, src, K + 1});//想集合添加一个记录费用、起点和中转站+1的数组 //K + 1是还可以走过站点的个数 while(!heap.isEmpty())//数组为空直接返回-1 { int[] cur = heap.poll();//得到集合当中添加的数组 int price = cur[0], place = cur[1], remainStops = cur[2]; if(place == dst)//起点等于v中点 return price;//返回0费用0 if(remainStops > 0)//中转次数》0(至少执行一次,因为remain====k+1) { for(int i = 0; i < n; i++)//小于城市数量 { if(g[place][i] > 0)//表示起点----终点的中转路线是否存在 { heap.offer(new int[]{price + g[place][i], i, remainStops - 1}); //如果存在 计算路费、起点的值、中转站-1 } } } } return -1; } }
790. 多米诺和托米诺平铺
描述:

思路:

791. 自定义字符串排序
描述:

思路:一种巧妙的实现方法是统计 T 中每个字符出现的次数,把结果存储在数组 count 中,count[char] 表示字符 char 出现的次数。然后把在 S 中出现的字符按照在 S 中的相对顺序排列,剩余字符添加到当前字符串的后面,最终排好序的字符串顺序为 S + (未在 S 中出现的字符)。
792. 匹配子序列的单词数
描述:

思路:桶排序,(放弃。。。)
795. 区间子数组个数
描述:

思路:
定义dp数组,dp[i]标识以A[i]结尾的符合条件的子数组个数,那么可以分三种情况讨论
A[i]在L和R之间,那么dp[i]的值为i-rpos,其中rpos是i之前第一个大于R的元素位置
A[i]小于L,dp[i] = dp[i-1],如果i为0则dp[i]等于0.
A[i]大于R,则dp[i] = 0.
将所有dp[i]加和就是要返回的结果.
797. 所有可能的路径
描述:

思路:深度优先。
799. 香槟塔
描述;

思路:倒满第一个层需要1背,前两层需要3杯,前3层需要6个。找到前几层是满的,然后剩余的从第i层分2i个支流流入i+1层的被子,除了边界流入一流,其余都是2流。
