[数值计算] QR分解 - 走看看

zoukankan html css js c++ java

[数值计算] QR分解
https://zhuanlan.zhihu.com/p/84415000

0. 为什么要用QR分解

$Ax=b, Ainmathbb{R}^{m imes n}$ 的问题可以分成3类：
- 情况1：A是方阵，m=n
- 情况2：A是over-determined的，m>n
- 情况3：A是under-determined的，m<n
在[数值计算] 条件数的例子2里，遇到的情况1（A是方阵），通过构造拉格朗日插值来使得对A求逆足够稳定。对于一般的情况下，解决思路是使用LU（LUP）分解来解决稳定性问题，在前一篇文中已经简介过了[数值计算] LU分解、LUP分解、Cholesky分解。

对于后两种情况， [数值计算] 数据拟合——线性最小二乘法分析了用正规方程组求解over-determined以及under-determined的问题。但在文中也提到了，对于over-determined的线性最小二乘问题，正规方程组是不稳定的，通常需要用QR分解来处理：

理论很美好，在小数据量的时候没问题，然而直接使用正规方程组求解会在数据量大(e.g. data size > 100)的时候不稳定numerically unstable。原因是需要对 $A^TA$ 求逆，而A我们都知道是Vandermonde矩阵的一部分，本身就是poorly conditioned，而 $A^TA$ 只会更糟糕。解决的方法是使用QR分解，这也是Python MATLAB求解线性最小二乘问题的方法。

1. QR分解

1.1 定义

一个矩阵 $A in mathbb{R}^{m imes n}, mge n$ 可以被分解成 $A = QR$ ，其中：
- $Qin mathbb{R}^{m imes m}$ 是正交矩阵
- $R equiv egin{bmatrix} hat{R} \ 0 end{bmatrix} in mathbb{R}^{m imes n}$
- $hat{R} in mathbb{R}^{n imes n}$ 是上三角矩阵
1.2 正交矩阵的性质
- $Q^T Q = QQ^T=I$
- 左乘一个正交矩阵对欧式范数的结果不影响（在下面证明eq.2的时候会用到）
$|| Qv ||_2^2 = v^TQ^TQv = v^Tv = || v ||_2^2 ag{1}$

1.3 从QR分解角度看线性最小二乘

对于一个over-determined线性最小二乘问题 $Axsimeq b$ ，其目标函数是 $egin{align} phi(x) = || r(x) ||_2^2 &= || b - Ax ||_2^2 = || b - Qegin{bmatrix}hat{R} \ 0end{bmatrix} x ||_2^2 \ &= || Q^T (b - Qegin{bmatrix}hat{R} \ 0end{bmatrix} x) ||_2^2 \ &= || Q^Tb - egin{bmatrix}hat{R} \ 0end{bmatrix} x ||_2^2 end{align} ag{2}$

这里 $Qin mathbb{R}^{m imes m}$ ， $Qbin mathbb{R}^{m imes 1}$ ， $egin{bmatrix}hat{R} \ 0end{bmatrix} in mathbb{R}^{m imes n}$ ， $egin{bmatrix}hat{R} \ 0end{bmatrix}x in mathbb{R}^{m imes 1}$ 。

如果把 $Q^Tb$ 拆分成上下两部分，形式 $egin{bmatrix}hat{R} \ 0end{bmatrix}$ 类似， $Q^Tb = egin{bmatrix} c_1\c_2 end{bmatrix}, where c_1 in mathbb{R}^n, c_2inmathbb{R}^{m-n}$ 。那么目标函数可以写成下面的形式：

$|| r(x) ||_2^2 = || c_1 - hat{R}x ||_2^2 + || c_2||_2^2 ag{3}$

可以看到，我们只能最小化前一部分 $|| c_1 - hat{R}x ||_2^2$ 到0，即 $hat{R}x = c_1$ ， $|| r(x) ||_2^2$ 的最小值为 $|| c_2||_2^2$ 。这样处理之后就避免了求正规方程组中的 $(A^TA)^{-1}$ ，避免了条件数变成 $cond(A^TA) = cond(A)^2$ ，所以QR分解法更加数值稳定。

1.4 计算QR分解的方法

一共有三种：
- Gram–Schmidt Orthogonalization
- Householder Triangularization
- Givens Rotations
1.5 Gram–Schmidt Orthogonalization

1.5.1 Reduced QR分解

GSO构建正交矩阵 $Qin mathbb{R}^{m imes m}$ 的方法是从A矩阵的n个列（ $A_{:,j} in mathbb{R}^{m imes 1}$ ）中构建互相正交的基，先选定 $A_{:,0}$ 为第一个基，然后把第二列 $A_{:,1}$ 减去平行于 $A_{:,0}$ 的部分，剩下的垂直于 $A_{:,0}$ 的部分作为下一个基，以此类推，直到生成了n个基。

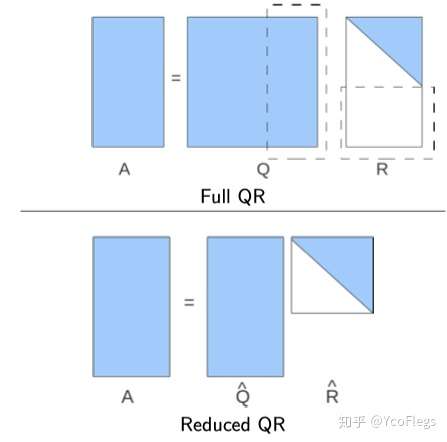
$egin{aligned} A_{:,0} &= r_{00}q_0 \ A_{:,1} &= r_{0,1}q_0 + r_{1,1}q_1 \ vdots\ A_{:,n-1} &= r_{0,n-1}q_0 + r_{1,n-1}q_1 + dots + r_{n-1,n-1}q_{n-1}\ A &= hat{Q}hat{R} end{aligned} ag{4}$

$egin{bmatrix} A_{:,0} | A_{:,1} | dots | A_{:,n-1} end{bmatrix} = egin{bmatrix} q_{0} | q_{1} | dots | q_{n-1} end{bmatrix} egin{bmatrix} r_{0,0} & r_{0,1} & dots & r_{0,n-1}\ & r_{1,1} & dots & r_{1,n-1}\ & & ddots & vdots \ & & & r_{n-1,n-1}\ end{bmatrix}\ ag{5}$

这个方法生成的 $hat{Q}in mathbb{R}^{m imes n}$ ， $hat{R} in mathbb{R}^{n imes n}$ ，和section1.1中定义的Q是方阵，R不是方阵有区别。这个结果被称为Reduced QR分解，因为m>n，所以只满足 $hat{Q}^That{Q} = I$ ，而不满足 $hat{Q}hat{Q}^T = I$ 。

Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

Reduced QR分解同样可以求解over-determined线性最小二乘问题。形式类似Full QR分解：

$hat{R}x = hat{Q}^T b ag{6}$

其中 $hat{R}x in mathbb{R}^{n imes 1}$ ， $hat{Q}^Tb in mathbb{R}^{n imes 1}$ 。

1.5.2 Full QR分解

为了实现定义中的完整的QR分解，需要把上面生成Q中的n个基拓展成m个互相正交的基。但此处并没有对额外的m-n个基的顺序有特殊要求，因此任意一种顺序都可以。另外还需要把 $hat{R}$ 下面加m-n行零矩阵。

在Python中，Reduced QR分解和Full QR分解对应于
q,r = np.linalg.qr(A) # reduced q,r = np.linalg.qr(A,mode="complete") # full
1.5.3 Classic Gram–Schmidt Orthogonalization算法 CGSO

观察Eq.4可以发现，其实每一步迭代都只有一个 $r_{j,j}$ 未知：左边 $A_{:,0}$ 已知，右边 $q_0 sim q_{j-1}$ 已知， q的系数们 $r_{0,j} sim r_{j-1,j}$ 可以用公式 $r_{i,j} = q_i^T A_{:,j}$ 求得。把 $r_{i,j} = q_i^T A_{:,j}$ 代入Eq.4，并整理可得

$r_{j,j}q_{j} = v_j= A_{:,j} - (q_0^T A_{:,j})q_0 - (q_1^T A_{:,j})q_1 - dots (q_{j-1}^T A_{:,j})q_{j-1} ag{7}$

因此 $q_j = frac{v_j}{||v_j||_2}$ ， $|r_{j,j}| = ||v_j||_2$ 。其中， $r_{j,j}$ 的符号不确定是因为，任意一个基方向反向之后，这个QR分解不会有任何问题，这个基仍然和其他基正交。为了计算方便，这里就规定 $r_{j,j} = ||v_j||_2$ 。

整理上面计算 $q_j$ 和 $r_{i,j}$ 的过程为算法的形式：

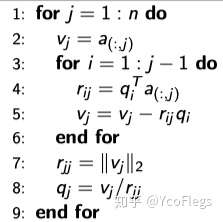Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

观察算法过程，可以发现，唯一可能在理论上出问题的情况就是，出现某个 $r_{j,j}$ =0，导致在算法第8行出现0在分母上的情况。因此只要 $Ainmathbb{R}^{m imes n}$ 是满秩的，且每个 $r_{jj}$ 都>0，那么reduced QR分解的结果是唯一的。

1.5.4 Modified Gram–Schmidt Orthogonalization算法 MGSO

由于CGSO对舍入误差很敏感，容易导致生成的基 $q_j$ 的正交性随着迭代越来越弱，因此引入改进的GSO。核心思想是，在每个 $q_j$ 生成后，直接把A剩下的列（下面算法第7行）都去掉 $q_j$ 的成分（下面算法的第8-9行）。因为只是把计算的顺序变了，所以理论上计算结果是一样的。

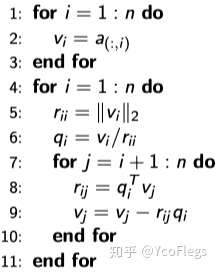Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

但是改进之后稳定性会好很多。从实际计算步骤上来看，CGSO和MGSO的区别在于，CGSO中，每次迭代新的一列 $v_i$ ，计算每个 $r_{i,j} = q_i^Tv_j$ 都是用的同一个 $v_j$ ，而MGSO计算 $r_{i,j}$ 的时候用的 $v_j$ 是已经减去前面j-1个基的分量之后的 $v_j$ 。

这样做的好处是：误差的传递是局部的。比如计算 $q_1$ 是精确的，计算 $q_2$ 出现误差，即， $q_2$ 在 $q_1$ 上存在一个微小分量。按照CGSO，接下来要分别计算 $v_3$ 在 $q_1$ 和 $q_2$ 的分量，最终 $q_1^Tv_3 e 0, q_2^Tv_3 e 0$ ；而MGSO则先计算 $v_3$ 在 $q_1$ 上的分量，去除掉这个分量之后成为 $v_3'$ ，再计算并去除 $v_3'$ 在 $q_2$ 上的分量得到最终的 $v_3''$ ，此时如果计算是精确的，那么至少可以保证 $v_3'' perp q_2$ 。

直观理解参考下面这张图，在三维xyz坐标系里， $q_2'$ 是带误差的 $q_2$ 。用CGSO处理 $q_2'$ 的时候， $v_3$ 用的是初始值 $(1,1,1)$ ，包含了 $q_1$ 和 $q_2$ 两个方向的误差，而用MGSO处理 $q_2'$ 的时候， $v_3$ 用的是去掉 $q_1$ 分量之后的 $v_3' = (0,1,1)$ ，只有 $q_1$ 方向的误差。

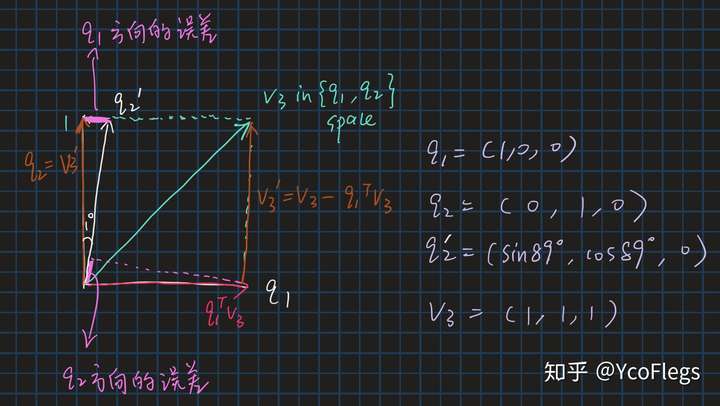
公式上计算这些误差参考The modified Gram-Schmidt procedure：

Credit to https://www.math.uci.edu/~ttrogdon/105A/html/Lecture23.html

1.6 Givens Rotations

1.6.1 Givens Rotation Matrix

$G(i,j, heta) = egin{bmatrix} 1 & dots & 0 & dots & 0 & dots & 0\ vdots & ddots & vdots & ddots & vdots & ddots & vdots\ 0 & dots & cos heta & dots & sin heta & dots & 0\ vdots & ddots & vdots & ddots & vdots & ddots & vdots\ 0 & dots & -sin heta & dots & cos heta & dots & 0\ vdots & ddots & vdots & ddots & vdots & ddots & vdots\ 0 & dots & 0 & dots & 0 & dots & 1\ end{bmatrix} ag{8}$

$egin{aligned} i &< j \ G_{i,i} &= c\ G_{j,j} &= c\ G_{i,j} &= s\ G_{j,i} &= -s\ G_{k,k} &= 1, for k e i or j\ G_{t,s} &= 0, otherwise end{aligned} ag{9}$

1.6.2 Givens Rotations的作用

对于一个矩阵 $Ain mathbb{R}^{m imes n}, mge n$ ，对于第i列的第j和k行 $A_{i,j},A_{i,k}, j<k$ ，如果 $A_{i,k}$ 元素不为0，可以通过一个Givens Rotation把它转换成0。

$egin{bmatrix} c & s\ -s & c end{bmatrix} egin{bmatrix} A_{i,j}\ A_{i,k} end{bmatrix} = egin{bmatrix} alpha\ 0 end{bmatrix}\ alpha = sqrt{A_{i,j}^2 + A_{i,k}^2 }\ c = frac{A_{i,j}}{alpha}\ s = frac{A_{i,k}}{alpha}\ ag{10}$

当 $A_{i,j}$ 或者 $A_{i,k}$ 很小或者很大，且它们的平方不是用float表示的时候，对它们求平方会导致上溢出或者下溢出。因此更好的公式是：
- 如果 $|A_{i,j}| > | A_{i,k}|$ ，那么设 $t = A_{i,k}/A_{i,j}$
$c = frac{1}{sqrt{1+t^2}}, s = ct$
- 如果 $|A_{i,j}| < | A_{i,k}|$ ，那么设 $au = A_{i,j}/A_{i,k}$
$s = frac{1}{sqrt{1+ au^2}}, c = s au$

不过这个问题基本只有在设计package造轮子的时候才会遇到，所以通常用Eq.10不会引起问题。详见Scientific Computing - Heath的第128页。

另外，在涉及反三角的数值运算的时候，建议使用atan2替代atan，范围更大，更稳定。例如atan2(y,x)会返回一个(x,y)向量和正x轴的夹角。

the difference between atan and atan2 in C++?stackoverflow.com wikipedia Atan2en.wikipedia.org

1.6.3 Givens Rotations 算法

对于一个稠密的矩阵 $Ain mathbb{R}^{m imes n}, mge n$ ，逐渐把A消元成R（参考1.5.1的full QR的图）。

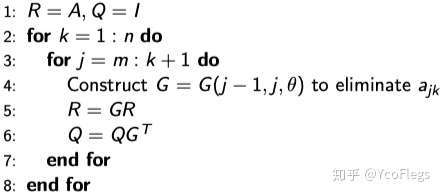Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

注意第三行的循环，j是从大到小的迭代。

1.6.4 Givens Rotations 优势

当A是稠密矩阵，Givens Rotations并没有比另外两种算法更高效，但如果A是稀疏矩阵，那么Givens Rotations大小为0的元素可以直接被忽略。另一个优势是，Givens Rotations更容易并行化，因为Givens Rotations只对两个元素进行操作，处理不同列的时候可以完全的独立。
查看全文

相关阅读:
【GC概述以及查看堆内存使用】Java内存管理和GC学习
 Spring的发展【一】
struts ValueStack 详解
 Mybatis常见面试题(转)
【Java基础】Java运算符优先级
 【Java基础】基本类型与运算【重要】
【Java基础】JAVA不可变类(immutable)机制与String的不可变性
 【Java基础】Java基本数据类型与位运算
 【Tomcat】tomcat配置多域名和虚拟路径
 【Tomcat】Tomcat替换猫的图片

原文地址：https://www.cnblogs.com/dhcn/p/14840472.html

Copyright © 2011-2022 走看看