二叉树

一、定义

二叉树是n（n>=0）个结点的有限集合，该集合或者为空集（空二叉树），或者由一个根结点和两棵互不相交的，分别称为跟结点的左子树和右子树的二叉树组成。

1.二叉树特点

• 每个结点最多有两棵子树，所以二叉树的度不大于2.
• 左子树和右子树是有顺序的，次序不能颠倒。
• 即使树中某结点只有一棵树，也要区分它是左子树还是右子树。

2.二叉树的五种基本形态

• 空二叉树
• 只有一个根结点二叉树
• 根结点只有左子树
• 根结点只有右子树
• 根结点既有左子树又有右子树

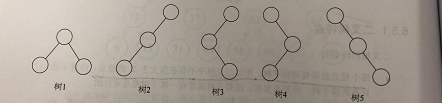
 3.特殊二叉树

          1.斜树

　　　所有结点的只有左子树的二叉树称为左斜树。所有结点都是只有右子树的二叉树称为右斜树。

          2.满二叉树

　　　在一棵二叉树中，所有分支结点都存在左子树和右子树，并且所有的叶结点都在同一层，这样的二叉树称为满二叉树。（满二叉树的叶子都在最下一层；非叶子的结点度都为2；在同样深度的二叉树中其结点个数最多，叶子结点数也最多）

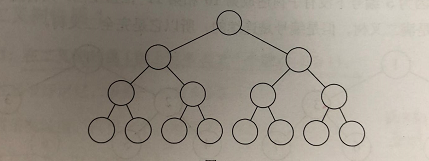
　　   3.完全二叉树

　　   对一棵具有n个结点的二叉树按层次序编号，如果编号为i的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同，则该二叉树称为完全二叉树。

　

        完全二叉树特点：

• 叶子结点只能出现在最下两层；
• 最下层的叶子结点一定集中在左部连接位置；
• 倒数第二层若出现叶子结点，一定在都在右部连续位置；
• 同样结点数的二叉树，完全二叉树的深度最小；
• 如果结点度为1，则该结点只有左孩子。

二、二叉树的性质

1. 在二叉树的第i层上至多有2^n-1个结点；
2. 深度为k的二叉树至多有2ⁿ-1个结点；
3. 对任何一棵二叉树T，如果其终端结点有N₀个，度为2 的结点数为N1个。则N₀=N₁ +1;
4. 具有N个结点的完全二叉树的深度为[log₂n]+1([x]表示不大于x的最大整数）
5. 如果对一棵有n个结点的完全二叉树的结点按结点层次序编号。对于任一结点i（1~n）有：

• • 如果i=1；则结点i是根结点，无双亲；如果i大于1则其双亲是结点[i/2];
  • 如果2i>n,则结点i无左孩子；否则其左孩子是结点2i；
  • 如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1；

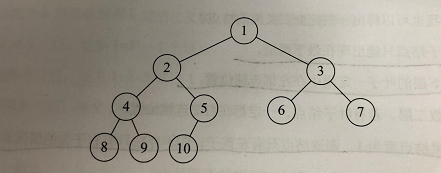
 三、二叉树的遍历

#include "stdio.h"          
#include "stdlib.h"     
#include "time.h"  
#include<iostream>
using namespace std;
typedef char ElemType;/* ElemType类型根据实际情况而定，这里假设为char */
//二叉树链表结点的定义
typedef struct BiNode
{
    ElemType data;//结点数据
    struct BiNode *lchild, *rchild;//左孩子右孩子
}BiNode,*BiTree;
//二叉树的创建最好使用前序遍历发
void CreaterBiTree(BiTree* T)
{
    ElemType ch;
    cin >> ch;
    if (ch == '#')
    {
        *T = nullptr;//无叶子结点
    }
    else
    {
        *T = (BiTree)malloc(sizeof(BiNode));
        if (!*T)
            exit(-1);
        (*T)->data = ch;//生成结点
        CreaterBiTree(&(*T)->lchild);//构造左子树
        CreaterBiTree(&(*T)->rchild);//构造右子树
    }
}
//结点遍历
void visit(char c,int level)
{
    cout << "第" << level << "层 "<< "  "<< c << endl;
}

//前序递归遍历
void preOrderTraverse(BiTree T,int level)
{
    if (T == nullptr)
        return;
    visit(T->data, level);
    preOrderTraverse(T->lchild, level+1);
    preOrderTraverse(T->rchild, level+1);
}
//中序递归遍历
void InOrderTraverse(BiTree T, int level)
{
    if (T == nullptr)
        return;  
    InOrderTraverse(T->lchild, level + 1);
    visit(T->data, level);
    InOrderTraverse(T->rchild, level + 1);
}
//后序递归遍历
void PostOrderTraverse(BiTree T, int level)
{
    if (T == nullptr)
        return;
    PostOrderTraverse(T->lchild, level + 1);
    PostOrderTraverse(T->rchild, level + 1);
    visit(T->data, level);
}
int main()
{
    BiTree T = nullptr;
    int level = 1;
    CreaterBiTree(&T);
    InOrderTraverse(T, level);
    cout << endl;
    preOrderTraverse(T, level);
    cout << endl;
    PostOrderTraverse(T, level);
   
    return 0;
}