Codeforces 592

题目链接：http://codeforces.com/contest/592/problem/B

B. The Monster and the Squirrel

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Ari the monster always wakes up very early with the first ray of the sun and the first thing she does is feeding her squirrel.

Ari draws a regular convex polygon on the floor and numbers it's vertices 1, 2, ..., n in clockwise order. Then starting from the vertex 1she draws a ray in the direction of each other vertex. The ray stops when it reaches a vertex or intersects with another ray drawn before. Ari repeats this process for vertex 2, 3, ..., n (in this particular order). And then she puts a walnut in each region inside the polygon.

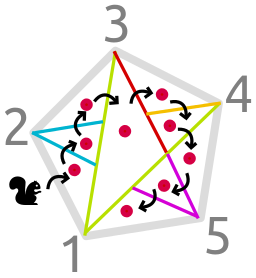
Ada the squirrel wants to collect all the walnuts, but she is not allowed to step on the lines drawn by Ari. That means Ada have to perform a small jump if she wants to go from one region to another. Ada can jump from one region P to another region Q if and only if P and Q share a side or a corner.

Assuming that Ada starts from outside of the picture, what is the minimum number of jumps she has to perform in order to collect all the walnuts?

Input

The first and only line of the input contains a single integer n (3 ≤ n ≤ 54321) - the number of vertices of the regular polygon drawn by Ari.

Output

Print the minimum number of jumps Ada should make to collect all the walnuts. Note, that she doesn't need to leave the polygon after.

Examples

input

5

output

9

input

3

output

1

Note

One of the possible solutions for the first sample is shown on the picture above.

找规律。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    long long n;
    cin>>n;
    cout<<(n-2)*(n-2)<<endl;
}

─────────────────────────────────────────────────────────────────────────────────────────────

题目链接：http://codeforces.com/contest/592/problem/C

C. The Big Race

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Vector Willman and Array Bolt are the two most famous athletes of Byteforces. They are going to compete in a race with a distance of Lmeters today.

Willman and Bolt have exactly the same speed, so when they compete the result is always a tie. That is a problem for the organizers because they want a winner.

While watching previous races the organizers have noticed that Willman can perform only steps of length equal to w meters, and Bolt can perform only steps of length equal to b meters. Organizers decided to slightly change the rules of the race. Now, at the end of the racetrack there will be an abyss, and the winner will be declared the athlete, who manages to run farther from the starting point of the the racetrack (which is not the subject to change by any of the athletes).

Note that none of the athletes can run infinitely far, as they both will at some moment of time face the point, such that only one step further will cause them to fall in the abyss. In other words, the athlete will not fall into the abyss if the total length of all his steps will be less or equal to the chosen distance L.

Since the organizers are very fair, the are going to set the length of the racetrack as an integer chosen randomly and uniformly in range from 1 to t (both are included). What is the probability that Willman and Bolt tie again today?

Input

The first line of the input contains three integers t, w and b (1 ≤ t, w, b ≤ 5·1018) — the maximum possible length of the racetrack, the length of Willman's steps and the length of Bolt's steps respectively.

Output

Print the answer to the problem as an irreducible fraction . Follow the format of the samples output.

The fraction  (p and q are integers, and both p ≥ 0 and q > 0 holds) is called irreducible, if there is no such integer d > 1, that both pand q are divisible by d.

Examples

input

10 3 2

output

3/10

input

7 1 2

output

3/7

Note

In the first sample Willman and Bolt will tie in case 1, 6 or 7 are chosen as the length of the racetrack.

题意：

两个人跑步比赛，一个人一步只能走w米，一个人一步只能走b米；

终点位置可以在整数1~t里面随便选择一个；

终点之后都是陷阱，两个人比赛但两个人都不想死，所以不能越过终点，在这种情况下，谁走的远，就算谁赢；

然后问你选择平局的概率是多少。

题解：

算算样例，可以看出所有最小公倍数情况的终点都能产生平局；

我们设tail=min(w,b)-1，可以看出，1~tail位置的终点也产生平局，每个最小公倍数终点后面tail个位置也能产生平局；

那么我们就围绕这个进行计算，可以按照1~t里有多少个lcm(w,b)整数倍终点进行分类考虑；

不过有一个错误点就是lcm(w,b)超过unsigned long long范围的情况，

这样一来，因为t的范围限制，lcm(w,b)必然大于t了，只需要在前面特判一下lcm(w,b)>t的情况即可，

具体怎么特判，lcm(w,b) = (w*b) / gcd(w,b) > t，两边取对数进行比较即可。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long llu;
inline llu gcd(llu m,llu n){return n?gcd(n,m%n):m;}
llu lcm(llu m,llu n){return m/gcd(m,n)*n;}
void output(llu p,llu q)
{
    llu pq_gcd=gcd(p,q);
    cout<<p/pq_gcd<<"/"<<q/pq_gcd<<endl;
}
bool check(llu t,llu w,llu b)
{
    return log(w*1.0)+log(b*1.0)-log(gcd(w,b)*1.0)>log(t*1.0);
}
int main()
{
    llu t,w,b;
    cin>>t>>w>>b;

    llu tail=min(w,b)-1;//tail>=0

    if(check(t,w,b))//判断lcm(w,b)>t?
    {
        output(min(tail,t),t);
        return 0;
    }

    llu wb_lcm=lcm(w,b);
    llu cnt=t/wb_lcm;
    if(cnt==0)
    {
        if(t<=tail)
        {
            cout<<"1/1"<<endl;
            return 0;
        }
        else
        {
            output(tail,t);
            return 0;
        }
    }
    else if(cnt==1)
    {
        llu ed=min(t%wb_lcm,tail)+1;
        output(tail+ed,t);
        return 0;
    }
    else
    {
        llu ed=min(t%wb_lcm,tail)+1;
        output(tail+(cnt-1)*(tail+1)+ed,t);
        return 0;
    }
}